| Class | Parsing grammars that are PEG |
|---|---|
| Data structure | String |
| Worst-case performance | or without special handling of iterative combinator |
| Best-case performance |
|
| Average performance | |
| Worst-case space complexity |
The Packrat parser is a type of parser that shares similarities with the recursive descent parser in its construction. However, it differs because it takes parsing expression grammars (PEGs) as input rather than LL grammars.
In 1970, Alexander Birman laid the groundwork for packrat parsing by introducing the "TMG recognition scheme" (TS), and "generalized TS" (gTS). TS was based upon Robert M. McClure's TMG compiler-compiler, and gTS was based upon Dewey Val Schorre's META compiler-compiler. Birman's work was later refined by Aho and Ullman; and renamed as Top-Down Parsing Language (TDPL), and Generalized TDPL (GTDPL), respectively. These algorithms were the first of their kind to employ deterministic top-down parsing with backtracking.
Bryan Ford developed PEGs as an expansion of GTDPL and TS. Unlike CFGs, PEGs are unambiguous and can match well with machine-oriented languages. PEGs, similar to GTDPL and TS, can also express all LL(k) and LR(k). Bryan also introduced Packrat as a parser that uses memoization techniques on top of a simple PEG parser. This was done because PEGs have an unlimited lookahead capability resulting in a parser with exponential time performance in the worst case.
Packrat keeps track of the intermediate results for all mutually recursive parsing functions. Each parsing function is only called once at a specific input position. In some instances of packrat implementation, if there is insufficient memory, certain parsing functions may need to be called multiple times at the same input position, causing the parser to take longer than linear time.
Syntax
See also: Parsing expression grammar § SyntaxThe packrat parser takes in input the same syntax as PEGs: a simple PEG is composed of terminal and nonterminal symbols, possibly interleaved with operators that compose one or several derivation rules.
Symbols
- Nonterminal symbols are indicated with capital letters (e.g., )
- Terminal symbols are indicated with lowercase (e.g., )
- Expressions are indicated with lower-case Greek letter (e.g., )
- Expressions can be a mix of terminal symbols, nonterminal symbols and operators
Operators
| Operator | Semantics |
|---|---|
| Sequence
|
Success: If and are recognized
Failure: If or are not recognized Consumed: and in case of success |
| Ordered choice
|
Success: If any of is recognized starting from the left
Failure: All of do not match Consumed: The atomic expression that has generated a success so if multiple succeed the first one is always returned |
| And predicate
|
Success: If is recognized
Failure: If is not recognized Consumed: No input is consumed |
| Not predicate
|
Success: If is not recognized
Failure: If is recognized Consumed: No input is consumed |
| One or more
|
Success: Try to recognize one or multiple time
Failure: If is not recognized Consumed: The maximum number that is recognized |
| Zero or more
|
Success: Try to recognize zero or multiple time
Failure: Cannot fail Consumed: The maximum number that is recognized |
| Zero or one
|
Success: Try to recognize zero or once
Failure: Cannot fail Consumed: if it is recognized |
| Terminal range
[] |
Success: Recognize any terminal that are inside the range . In the case of , can be any letter from h to z
Failure: If no terminal inside of can be recognized Consumed: if it is recognized |
| Any character
|
Success: Recognize any character in the input
Failure: If no character in the input Consumed: any character in the input |
Rules
A derivation rule is composed by a nonterminal symbol and an expression .
A special expression is the starting point of the grammar. In case no is specified, the first expression of the first rule is used.
An input string is considered accepted by the parser if the is recognized. As a side-effect, a string can be recognized by the parser even if it was not fully consumed.
An extreme case of this rule is that the grammar matches any string.
This can be avoided by rewriting the grammar as
Example
This grammar recognizes a palindrome over the alphabet , with an optional digit in the middle.
Example strings accepted by the grammar include: and .
Left recursion
Left recursion happens when a grammar production refers to itself as its left-most element, either directly or indirectly. Since Packrat is a recursive descent parser, it cannot handle left recursion directly. During the early stages of development, it was found that a production that is left-recursive can be transformed into a right-recursive production. This modification significantly simplifies the task of a Packrat parser. Nonetheless, if there is an indirect left recursion involved, the process of rewriting can be quite complex and challenging. If the time complexity requirements are loosened from linear to superlinear, it is possible to modify the memoization table of a Packrat parser to permit left recursion, without altering the input grammar.
Iterative combinator
The iterative combinator , , needs special attention when used in a Packrat parser. As a matter of fact, the use of iterative combinators introduces a secret recursion that does not record intermediate results in the outcome matrix. This can lead to the parser operating with a superlinear behaviour. This problem can be resolved apply the following transformation:
| Original | Translated |
|---|---|
With this transformation, the intermediate results can be properly memoized.
Memoization technique
Memoization is an optimization technique in computing that aims to speed up programs by storing the results of expensive function calls. This technique essentially works by caching the results so that when the same inputs occur again, the cached result is simply returned, thus avoiding the time-consuming process of re-computing. When using packrat parsing and memoization, it's noteworthy that the parsing function for each nonterminal is solely based on the input string. It does not depend on any information gathered during the parsing process. Essentially, memoization table entries do not affect or rely on the parser's specific state at any given time.
Packrat parsing stores results in a matrix or similar data structure that allows for quick look-ups and insertions. When a production is encountered, the matrix is checked to see if it has already occurred. If it has, the result is retrieved from the matrix. If not, the production is evaluated, the result is inserted into the matrix, and then returned. When evaluating the entire matrix in a tabular approach, it would require space. Here, represents the number of nonterminals, and represents the input string size.
In a naïve implementation, the entire table can be derived from the input string starting from the end of the string.
The Packrat parser can be improved to update only the necessary cells in the matrix through a depth-first visit of each subexpression tree. Consequently, using a matrix with dimensions of is often wasteful, as most entries would remain empty. These cells are linked to the input string, not to the nonterminals of the grammar. This means that increasing the input string size would always increase memory consumption, while the number of parsing rules changes only the worst space complexity.
Cut operator
Another operator called cut has been introduced to Packrat to reduce its average space complexity even further. This operator utilizes the formal structures of many programming languages to eliminate impossible derivations. For instance, control statements parsing in a standard programming language is mutually exclusive from the first recognized token, e.g.,.
| Operator | Semantics |
|---|---|
| Cut
|
if is recognized but is not, skip the evaluation of the alternative.
In the first case don't evaluate if was recognized The second rule is can be rewritten as and the same rules can be applied. |
When a Packrat parser uses cut operators, it effectively clears its backtracking stack. This is because a cut operator reduces the number of possible alternatives in an ordered choice. By adding cut operators in the right places in a grammar's definition, the resulting Packrat parser only needs a nearly constant amount of space for memoization.
The algorithm
Sketch of an implementation of a Packrat algorithm in a Lua-like pseudocode.
INPUT(n) -- return the character at position n
RULE(R : Rule, P : Position )
entry = GET_MEMO(R,P) -- return the number of elements previously matched in rule R at position P
if entry == nil then
return EVAL(R, P);
end
return entry;
EVAL(R : Rule, P : Position )
start = P;
for choice in R.choices -- Return a list of choice
acc=0;
for symbol in choice then -- Return each element of a rule, terminal and nonterminal
if symbol.is_terminal then
if INPUT(start+acc) == symbol.terminal then
acc = acc + 1; --Found correct terminal skip pass it
else
break;
end
else
res = RULE(symbol.nonterminal , start+acc ); -- try to recognize a nonterminal in position start+acc
SET_MEMO(symbol.nonterminal , start+acc, res ); -- we memoize also the failure with special value fail
if res == fail then
break;
end
acc = acc + res;
end
if symbol == choice.last -- check if we have matched the last symbol in a choice if so return
return acc;
end
end
return fail; --if no choice match return fail
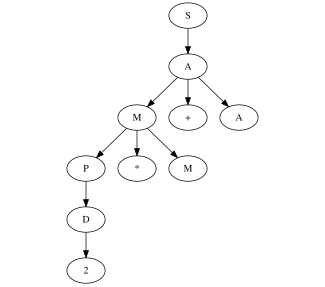
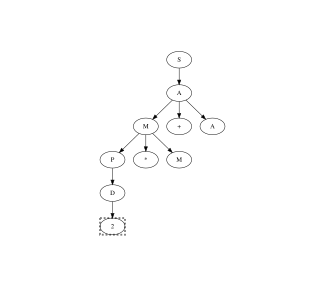
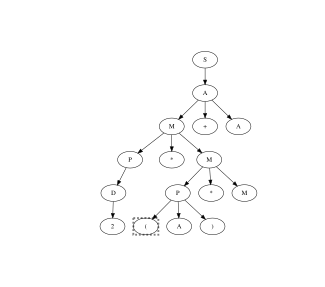
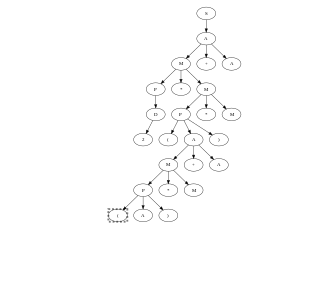
Example
Given the following context, a free grammar that recognizes simple arithmetic expressions composed of single digits interleaved by sum, multiplication, and parenthesis.
Denoted with the line terminator we can apply the packrat algorithm
Implementation
See also: Comparison of parser generators § Parsing expression grammars, deterministic boolean grammars| Name | Parsing algorithm | Output languages | Grammar, code | Development platform | License |
|---|---|---|---|---|---|
| AustenX | Packrat (modified) | Java | Separate | All | Free, BSD |
| Aurochs | Packrat | C, OCaml, Java | Mixed | All | Free, GNU GPL |
| Canopy | Packrat | Java, JavaScript, Python, Ruby | Separate | All | Free, GNU GPL |
| CL-peg | Packrat | Common Lisp | Mixed | All | Free, MIT |
| Drat! | Packrat | D | Mixed | All | Free, GNU GPL |
| Frisby | Packrat | Haskell | Mixed | All | Free, BSD |
| grammar::peg | Packrat | Tcl | Mixed | All | Free, BSD |
| IronMeta | Packrat | C# | Mixed | Windows | Free, BSD |
| PEGParser | Packrat (supporting left-recursion and grammar ambiguity) | C++ | Identical | All | Free, BSD |
| Narwhal | Packrat | C | Mixed | POSIX, Windows | Free, BSD |
| neotoma | Packrat | Erlang | Separate | All | Free, MIT |
| OMeta | Packrat (modified, partial memoization) | JavaScript, Squeak, Python | Mixed | All | Free, MIT |
| PackCC | Packrat (modified, left-recursion support) | C | Mixed | All | Free, MIT |
| Packrat | Packrat | Scheme | Mixed | All | Free, MIT |
| Pappy | Packrat | Haskell | Mixed | All | Free, BSD |
| Parsnip | Packrat | C++ | Mixed | Windows | Free, GNU GPL |
| PEG.js | Packrat (partial memoization) | JavaScript | Mixed | All | Free, MIT |
| Peggy | Packrat (partial memoization) | JavaScript | Mixed | All | Free, MIT |
| Pegasus | Recursive descent, Packrat (selectively) | C# | Mixed | Windows | Free, MIT |
| PetitParser | Packrat | Smalltalk, Java, Dart | Mixed | All | Free, MIT |
| PyPy rlib | Packrat | Python | Mixed | All | Free, MIT |
| Rats! | Packrat | Java | Mixed | Java virtual machine | Free, GNU LGPL |
| go-packrat | Packrat | Go | Identical | All | GPLv3 |
See also
References
- ^ Ford, Bryan (2006). "Packrat Parsing: Simple, Powerful, Lazy, Linear Time". arXiv:cs/0603077.
- ^ Ford, Bryan (2004-01-01). "Parsing expression grammars". Proceedings of the 31st ACM SIGPLAN-SIGACT symposium on Principles of programming languages. POPL '04. New York, NY, USA: Association for Computing Machinery. pp. 111–122. doi:10.1145/964001.964011. ISBN 978-1-58113-729-3. S2CID 7762102.
- ^ Flodin, Daniel. "A Comparison Between Packrat Parsing and Conventional Shift-Reduce Parsing on Real-World Grammars and Inputs" (PDF).
- Mizushima, Kota; Maeda, Atusi; Yamaguchi, Yoshinori (2010-05-06). "Packrat parsers can handle practical grammars in mostly constant space". Proceedings of the 9th ACM SIGPLAN-SIGSOFT workshop on Program analysis for software tools and engineering. ACM. pp. 29–36. doi:10.1145/1806672.1806679. ISBN 978-1-4503-0082-7. S2CID 14498865.
- ^ Warth, Alessandro; Douglass, James R.; Millstein, Todd (2008-01-07). "Packrat parsers can support left recursion". Proceedings of the 2008 ACM SIGPLAN symposium on Partial evaluation and semantics-based program manipulation. PEPM '08. New York, NY, USA: Association for Computing Machinery. pp. 103–110. doi:10.1145/1328408.1328424. ISBN 978-1-59593-977-7. S2CID 2168153.
- Aho, Alfred V.; Lam, Monica S.; Sethi, Ravi; Ullman, Jeffrey D., eds. (2007). Compilers: principles, techniques, & tools (2nd ed.). Boston Munich: Pearson Addison-Wesley. ISBN 978-0-321-48681-3.
- Norvig, Peter (1991-03-01). "Techniques for automatic memoization with applications to context-free parsing". Computational Linguistics. 17 (1): 91–98. ISSN 0891-2017.
- Dubroy, Patrick; Warth, Alessandro (2017-10-23). "Incremental packrat parsing". Proceedings of the 10th ACM SIGPLAN International Conference on Software Language Engineering. SLE 2017. New York, NY, USA: Association for Computing Machinery. pp. 14–25. doi:10.1145/3136014.3136022. ISBN 978-1-4503-5525-4. S2CID 13047585.
- ^ Science, International Journal of Scientific Research in; Ijsrset, Engineering and Technology. "A Survey of Packrat Parser". A Survey of Packrat Parser.
- ^ Mizushima, Kota; Maeda, Atusi; Yamaguchi, Yoshinori (2010-05-06). "Packrat parsers can handle practical grammars in mostly constant space". Proceedings of the 9th ACM SIGPLAN-SIGSOFT workshop on Program analysis for software tools and engineering. PASTE '10. New York, NY, USA: Association for Computing Machinery. pp. 29–36. doi:10.1145/1806672.1806679. ISBN 978-1-4503-0082-7. S2CID 14498865.
- Maintained fork of PEG.js
External links
- Packrat Parsing: Simple, Powerful, Lazy, Linear Time
- Parsing Expression Grammars: A Recognition-Based Syntactic Foundation
| Parsing algorithms | |
|---|---|
| Top-down | |
| Bottom-up | |
| Mixed, other |
|
| Related topics | |
 or
or  without special handling of iterative combinator
without special handling of iterative combinator )
) )
) )
)

 and
and  are recognized
are recognized

 is recognized starting from the left
is recognized starting from the left





 ]
]
 that are inside the range
that are inside the range  . In the case of
. In the case of  ,
, 
 .
.
 is the starting point of the grammar. In case no
is the starting point of the grammar. In case no  can be recognized by the parser even if it was not fully consumed.
can be recognized by the parser even if it was not fully consumed.
 matches any string.
matches any string.


 , with an optional digit in the middle.
, with an optional digit in the middle.
 and
and  .
.




 matrix in a tabular approach, it would require
matrix in a tabular approach, it would require  space. Here,
space. Here,  represents the number of nonterminals, and
represents the number of nonterminals, and  represents the input string size.
represents the input string size.
 .
.

 if
if  and the same rules can be applied.
and the same rules can be applied.

 the line terminator we can apply the packrat algorithm
the line terminator we can apply the packrat algorithm














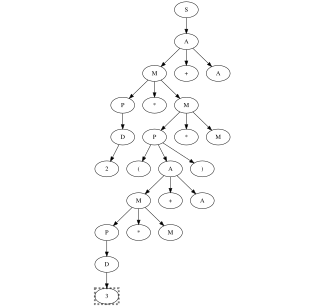


 inside
inside 
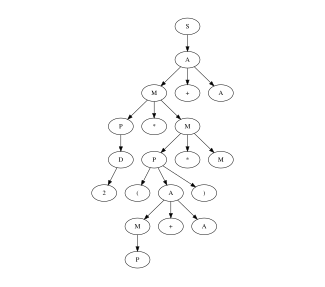


 from
from 

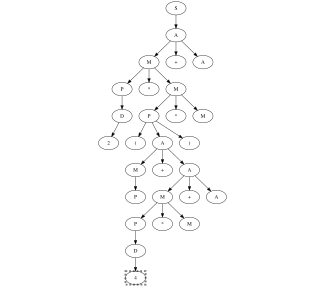


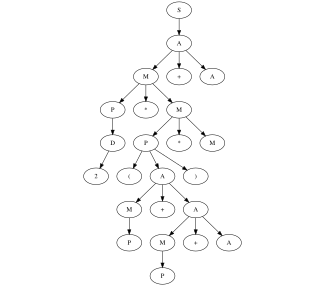




 from
from