Misplaced Pages

Parity measurement (also referred to as Operator measurement) is a procedure in quantum information science used for error detection in quantum qubits. A parity measurement checks the equality of two qubits to return a true or false answer, which can be used to determine whether a correction needs to occur. Additional measurements can be made for a system greater than two qubits. Because parity measurement does not measure the state of singular bits but rather gets information about the whole state, it is considered an example of a joint measurement. Joint measurements do not have the consequence of destroying the original state of a qubit as normal quantum measurements do. Mathematically speaking, parity measurements are used to project a state into an eigenstate of an operator and to acquire its eigenvalue.

Parity measurement is an essential concept of quantum error correction. From the parity measurement, an appropriate unitary operation can be applied to correct the error without knowing the beginning state of the qubit.

Parity and parity checking

A qubit is a two-level system, and when we measure one qubit, we can have either 1 or 0 as a result. One corresponds to odd parity, and zero corresponds to even parity. This is what a parity check is. This idea can be generalized beyond single qubits. This can be generalized beyond a single qubit and it is useful in QEC. The idea of parity checks in QEC is to have just parity information of multiple data qubits over one (auxiliary) qubit without revealing any other information. Any unitary can be used for the parity check. If we want to have the parity information of a valid quantum observable U, we need to apply the controlled-U gates between the ancilla qubit and the data qubits sequentially. For example, for making parity check measurement in the X basis, we need to apply CNOT gates between the ancilla qubit and the data qubits sequentially since the controlled gate in this case is a CNOT (CX) gate.

The unique state of the ancillary qubit is then used to determine either even or odd parity of the qubits. When the qubits of the input states are equal, an even parity will be measured, indicating that no error has occurred. When the qubits are unequal, an odd parity will be measured, indicating a single bit-flip error.

With more than two qubits, additional parity measurements can be performed to determine if the qubits are the same value, and if not, to find which is the outlier. For example, in a system of three qubits, one can first perform a parity measurement on the first and second qubit, and then on the first and third qubit. Specifically, one is measuring ${\displaystyle Z\otimes Z\otimes I}$ to determine if an ${\displaystyle X}$ error has occurred on the first two qubits, and then ${\displaystyle Z\otimes I\otimes Z}$ to determine if an ${\displaystyle X}$ error has occurred on the first and third qubits.

In a circuit, an ancillary qubit is prepared in the ${\displaystyle |0\rangle }$ state. During measurement, a CNOT gate is performed on the ancillary bit dependent on the first qubit being checked, followed by a second CNOT gate performed on the ancillary bit dependent on the second qubit being checked. If these qubits are the same, the double CNOT gates will revert the ancillary qubit to its initial ${\displaystyle |0\rangle }$ state, which indicates even parity. If these qubits are not the same, the double CNOT gates will alter the ancillary qubit to the opposite ${\displaystyle |1\rangle }$ state, which indicates odd parity. Looking at the ancillary qubits, a corresponding correction can be performed.

Alternatively, the parity measurement can be thought of as a projection of a qubit state into an eigenstate of an operator and to acquire its eigenvalue. For the ${\displaystyle Z\otimes Z\otimes I}$ measurement, checking the ancillary qubit in the basis ${\displaystyle |0\rangle \pm \ |1\rangle }$ will return the eigenvalue of the measurement. If the eigenvalue here is measured to be +1, this indicates even parity of the bits without error. If the eigenvalue is measured to be -1, this indicates odd parity of the bits with a bit-flip error.

Example

Alice, a sender, wants to transmit a qubit to Bob, a receiver. The state of any qubit that Alice would wish to send can be written as ${\displaystyle a\ |0\rangle +b\ |1\rangle }$ where ${\displaystyle a\ }$and ${\displaystyle b\ }$are coefficients. Alice encodes this into three qubits, so that the initial state she transmits is ${\displaystyle a\ |000\rangle +b\ |111\rangle }$. Following noise in the channel, the three qubits state can be seen in the following table with the corresponding probability:

State Changes following Noise in a Quantum Circuit

Qubit State	Probability	Ancillary Qubits	Correction
${\displaystyle (a\ |000\rangle +b\ |111\rangle )\ }$	${\displaystyle (1-p)^{3}}$	${\displaystyle |00\rangle }$	not needed
${\displaystyle (a\ |100\rangle +b\ |011\rangle )\ }$	${\displaystyle p(1-p)^{2}}$	${\displaystyle |11\rangle }$	apply ${\displaystyle \sigma _{x}}$ to first qubit
${\displaystyle (a\ |010\rangle +b\ |101\rangle )}$	${\displaystyle p(1-p)^{2}}$	${\displaystyle |10\rangle }$	apply ${\displaystyle \sigma _{x}}$ to second qubit
${\displaystyle (a\ |001\rangle +b\ |110\rangle )}$	${\displaystyle p(1-p)^{2}}$	${\displaystyle |01\rangle }$	apply ${\displaystyle \sigma _{x}}$ to third qubit
${\displaystyle (a\ |110\rangle +b\ |001\rangle )}$	${\displaystyle p^{2}(1-p)}$	${\displaystyle |01\rangle }$	apply ${\displaystyle \sigma _{x}}$ to third qubit
${\displaystyle (a\ |101\rangle +b\ |010\rangle )}$	${\displaystyle p^{2}(1-p)}$	${\displaystyle |10\rangle }$	apply ${\displaystyle \sigma _{x}}$ to second qubit
${\displaystyle (a\ |011\rangle +b\ |100\rangle )}$	${\displaystyle p^{2}(1-p)}$	${\displaystyle |11\rangle }$	apply ${\displaystyle \sigma _{x}}$ to first qubit
${\displaystyle (a\ |111\rangle +b\ |000\rangle )\ }$	${\displaystyle p^{3}}$	${\displaystyle |00\rangle }$	not needed

A parity measurement can be performed on the altered state, with two ancillary qubits storing the measurement. First, the first and second qubits' parity is checked. If they are equal, a ${\displaystyle |0\rangle }$ is stored in the first ancillary qubit. If they are not equal, a ${\displaystyle |1\rangle }$ is stored in the first ancillary qubit. The same action is performed comparing the first and third qubits, with the check being stored in the second ancillary qubit. Important to note is that we do not actually need to know the input qubit state, and can perform the CNOT operations indicating the parity without this knowledge. The ancillary qubits are what indicates what bit has been altered, and the ${\displaystyle \sigma _{x}}$ correction operation can be performed as needed.

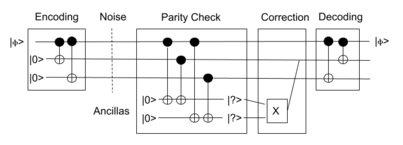
An easy way to visualize this is in the circuit above. First, the input state ${\displaystyle |\psi \rangle }$ is encoded into 3 bits, and parity checks are performed with subsequent error correction performed based on the results of the ancilla qubits at the bottom. Finally, decoding is performing to put get back to the same basis of the input state.

Parity check matrix

A parity check matrix for a quantum circuit can also be constructed using these principles. For some message x encoded as Gx, where G corresponds to the generator matrix, Hx = 0 where H is the parity matrix containing 0's and 1's for a situation where there is no error. However, if an error occurs at one component, then the pattern in the errors can be used to find which bit is incorrect.

Types of parity measurements

Two types of parity measurement are indirect and direct. Indirect parity measurements coincide with the typical way we think of parity measurement as described above, by measuring an ancilla qubit to determine the parity of the input bits. Direct parity measurements differ from the previous type in that a common mode with the parities coupled to the qubits is measured, without the need for an ancilla qubit. While indirect parity measurements can put a strain on experimental capacity, direct measurements may interfere with the fidelity of the initial states.

Example

For example, given a Hermitian and Unitary operator ${\displaystyle U}$ (whose eigenvalues are ${\displaystyle \pm 1}$) and a state ${\displaystyle |\psi \rangle }$, the circuit on the top right performs a Parity measurement on ${\displaystyle U}$. After the first Hadamard gate, the state of the circuit is

${\displaystyle {\frac {1}{\sqrt {2}}}(|0\rangle |\psi \rangle +|1\rangle |\psi \rangle )}$

After applying the controlled-U gate, the state of the circuit evolves to

${\displaystyle {\frac {1}{\sqrt {2}}}(|0\rangle |\psi \rangle +|1\rangle U|\psi \rangle )}$

After applying the second Hadamard gate, the state of the circuit turns into

${\displaystyle {\frac {1}{2}}|0\rangle (|\psi \rangle +U|\psi \rangle )+{\frac {1}{2}}|1\rangle (|\psi \rangle -U|\psi \rangle )}$

If the state of the top qubit after measurement is ${\displaystyle |0\rangle }$, then ${\displaystyle |\phi \rangle =|\psi \rangle +U|\psi \rangle }$; which is the ${\displaystyle +1}$ eigenstate of ${\displaystyle U}$. If the state of the top qubit is ${\displaystyle |1\rangle }$, then ${\displaystyle |\phi \rangle =|\psi \rangle -U|\psi \rangle }$; which is the ${\displaystyle -1}$ eigenstate of ${\displaystyle U}$.

Experiments and applications

In experiments, parity measurements are not only a mechanism for quantum error correction, but they can also help combat non-ideal conditions. Given the existent possibility for bit flip errors, there is an additional likelihood for errors as a result of leakage. This phenomenon is due to unused high-energy qubits becoming excited. It has been demonstrated in superconducting transmon qubits that parity measurements can be applied repetitively during quantum error correction to remove leakage errors. Repetitive parity measurements can be used to stabilize an entangled state and prevent leakage errors (which normally is not possible with typical quantum error correction), but the first group to accomplish this did so in 2020. By performing interleaving XX and ZZ checks, which can ultimately tell whether an X (bit), Y (iXZ), or Z (phase) flip error occurs. The outcomes of these parity measurements of ancilla qubits are used with Hidden Markov Models to complete leakage detection and correction.

References

1. ^ Steane, Andrew M. (2006). A tutorial on quantum error correction. Quantum Computers, Algorithms and Chaos, 1-32. https://www2.physics.ox.ac.uk/sites/default/files/ErrorCorrectionSteane06.pdf
2. Thekkadath, Guillaume (2017). Joint Measurements of Complementary Properties of Quantum Systems (Thesis thesis). Université d'Ottawa / University of Ottawa. doi:10.20381/ruor-20949.
3. ^ Nielsen, Michael A. (2010). Quantum computation and quantum information. Isaac L. Chuang (10th anniversary ed.). Cambridge: Cambridge University Press. ISBN 978-1-107-00217-3. OCLC 665137861.
4. Üstün, Gözde; Morello, Andrea; Devitt, Simon (2023), Single-Step Parity Check Gate Set for Quantum Error Correction, arXiv:2306.08849
5. ^ Devitt, Simon J.; Nemoto, Kae; Munro, William J. (2013). "Quantum error correction for beginners". Reports on Progress in Physics. 76 (7): 076001. arXiv:0905.2794. Bibcode:2013RPPh...76g6001D. doi:10.1088/0034-4885/76/7/076001. PMID 23787909. S2CID 206021660.
6. Royer, Baptiste; Puri, Shruti; Blais, Alexandre (2018-11-02). "Qubit parity measurement by parametric driving in circuit QED". Science Advances. 4 (11): eaau1695. arXiv:1802.10112. Bibcode:2018SciA....4.1695R. doi:10.1126/sciadv.aau1695. ISSN 2375-2548. PMC 6269160. PMID 30515454.
7. McEwen, M.; Kafri, D.; Chen, Z.; Atalaya, J.; Satzinger, K. J.; Quintana, C.; Klimov, P. V.; Sank, D.; Gidney, C.; Fowler, A. G.; Arute, F.; Arya, K.; Buckley, B.; Burkett, B.; Bushnell, N. (2021-03-19). "Removing leakage-induced correlated errors in superconducting quantum error correction". Nature Communications. 12 (1): 1761. arXiv:2102.06131. Bibcode:2021NatCo..12.1761M. doi:10.1038/s41467-021-21982-y. ISSN 2041-1723. PMC 7979694. PMID 33741936.
8. Bultink, C. C.; O'Brien, T. E.; Vollmer, R.; Muthusubramanian, N.; Beekman, M. W.; Rol, M. A.; Fu, X.; Tarasinski, B.; Ostroukh, V.; Varbanov, B.; Bruno, A.; DiCarlo, L. (2020-03-20). "Protecting quantum entanglement from leakage and qubit errors via repetitive parity measurements". Science Advances. 6 (12): eaay3050. arXiv:1905.12731. Bibcode:2020SciA....6.3050B. doi:10.1126/sciadv.aay3050. ISSN 2375-2548. PMC 7083610. PMID 32219159.

• Quantum information theory
• Quantum measurement
• Quantum computing