In algebraic topology, a peripheral subgroup for a space-subspace pair X ⊃ Y is a certain subgroup of the fundamental group of the complementary space, π1(X − Y). Its conjugacy class is an invariant of the pair (X,Y). That is, any homeomorphism (X, Y) → (X′, Y′) induces an isomorphism π1(X − Y) → π1(X′ − Y′) taking peripheral subgroups to peripheral subgroups.
A peripheral subgroup consists of loops in X − Y which are peripheral to Y, that is, which stay "close to" Y (except when passing to and from the basepoint). When an ordered set of generators for a peripheral subgroup is specified, the subgroup and generators are collectively called a peripheral system for the pair (X, Y).
Peripheral systems are used in knot theory as a complete algebraic invariant of knots. There is a systematic way to choose generators for a peripheral subgroup of a knot in 3-space, such that distinct knot types always have algebraically distinct peripheral systems. The generators in this situation are called a longitude and a meridian of the knot complement.
Full definition
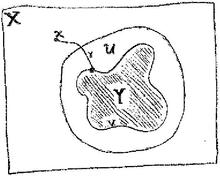
Let Y be a subspace of the path-connected topological space X, whose complement X − Y is path-connected. Fix a basepoint x ∈ X − Y. For each path component Vi of X − Y∩Y, choose a path γi from x to a point in Vi. An element ∈ π1(X − Y, x) is called peripheral with respect to this choice if it is represented by a loop in U ∪ ∪ iγi for every neighborhood U of Y. The set of all peripheral elements with respect to a given choice forms a subgroup of π1(X − Y, x), called a peripheral subgroup.
In the diagram, a peripheral loop would start at the basepoint x and travel down the path γ until it's inside the neighborhood U of the subspace Y. Then it would move around through U however it likes (avoiding Y). Finally it would return to the basepoint x via γ. Since U can be a very tight envelope around Y, the loop has to stay close to Y.
Any two peripheral subgroups of π1(X − Y, x), resulting from different choices of paths γi, are conjugate in π1(X − Y, x). Also, every conjugate of a peripheral subgroup is itself peripheral with respect to some choice of paths γi. Thus the peripheral subgroup's conjugacy class is an invariant of the pair (X, Y).
A peripheral subgroup, together with an ordered set of generators, is called a peripheral system for the pair (X, Y). If a systematic method is specified for selecting these generators, the peripheral system is, in general, a stronger invariant than the peripheral subgroup alone. In fact, it is a complete invariant for knots.
In knot theory
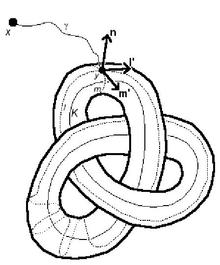
The peripheral subgroups for a tame knot K in R are isomorphic to Z ⊕ Z if the knot is nontrivial, Z if it is the unknot. They are generated by two elements, called a longitude and a meridian . (If K is the unknot, then is a power of , and a peripheral subgroup is generated by alone.) A longitude is a loop that runs from the basepoint x along a path γ to a point y on the boundary of a tubular neighborhood of K, then follows along the tube, making one full lap to return to y, then returns to x via γ. A meridian is a loop that runs from x to y, then circles around the tube, returns to y, then returns to x. (The property of being a longitude or meridian is well-defined because the tubular neighborhoods of a tame knot are all ambiently isotopic.) Note that every knot group has a longitude and meridian; if and are a longitude and meridian in a given peripheral subgroup, then so are · and , respectively (n ∈ Z). In fact, these are the only longitudes and meridians in the subgroup, and any pair will generate the subgroup.
A peripheral system for a knot can be selected by choosing generators and such that the longitude l has linking number 0 with K, and the ordered triple (m′,l′,n) is a positively oriented basis for R, where m′ is the tangent vector of m based at y, l′ is the tangent vector of l based at y, and n is an outward-pointing normal to the tube at y. (Assume that representatives l and m are chosen to be smooth on the tube and cross only at y.) If so chosen, the peripheral system is a complete invariant for knots, as proven in .

Example: Square knot versus granny knot
The square knot and the granny knot are distinct knots, and have non-homeomorphic complements. However, their knot groups are isomorphic. Nonetheless, it was shown in that no isomorphism of their knot groups carries a peripheral subgroup of one to a peripheral subgroup of the other. Thus the peripheral subgroup is sufficient to distinguish these knots.

Example: Trefoil versus mirror trefoil
The trefoil and its mirror image are distinct knots, and consequently there is no orientation-preserving homeomorphism between their complements. However, there is an orientation-reversing self-homeomorphism of R that carries the trefoil to its mirror image. This homeomorphism induces an isomorphism of the knot groups, carrying a peripheral subgroup to a peripheral subgroup, a longitude to a longitude, and a meridian to a meridian. Thus the peripheral subgroup is not sufficient to distinguish these knots. Nonetheless, it was shown in that no isomorphism of these knot groups preserves the peripheral system selected as described above. An isomorphism will, at best, carry one generator to a generator going the "wrong way". Thus the peripheral system can distinguish these knots.
Wirtinger presentation
It is possible to express longitudes and meridians of a knot as words in the Wirtinger presentation of the knot group, without reference to the knot itself.
References
- Fox, Ralph H., A quick trip through knot theory, in: M.K. Fort (Ed.), "Topology of 3-Manifolds and Related Topics", Prentice-Hall, NJ, 1961, pp. 120–167. MR0140099
- Waldhausen, Friedhelm (1968), "On irreducible 3-manifolds which are sufficiently large", Annals of Mathematics, Second Series, 87 (1): 56–88, doi:10.2307/1970594, ISSN 0003-486X, JSTOR 1970594, MR 0224099
- Dehn, Max, Die beiden Kleeblattschlingen, Mathematische Annalen 75 (1914), no. 3, 402–413.