Misplaced Pages

Physiologically based pharmacokinetic modelling

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
(Redirected from Physiologically-based pharmacokinetic modelling)
Graphic representation of a physiologically based whole body model. Here, it is dissected into seven tissue/organ compartments: brain, lungs and heart, pancreas, liver, gut, kidney and adipose/muscle tissue. Blood flows, Q, and concentration, , of a substance of interest are depicted.

Physiologically based pharmacokinetic (PBPK) modeling is a mathematical modeling technique for predicting the absorption, distribution, metabolism and excretion (ADME) of synthetic or natural chemical substances in humans and other animal species. PBPK modeling is used in pharmaceutical research and drug development, and in health risk assessment for cosmetics or general chemicals.

PBPK models strive to be mechanistic by mathematically transcribing anatomical, physiological, physical, and chemical descriptions of the phenomena involved in the complex ADME processes. A large degree of residual simplification and empiricism is still present in those models, but they have an extended domain of applicability compared to that of classical, empirical function based, pharmacokinetic models. PBPK models may have purely predictive uses, but other uses, such as statistical inference, have been made possible by the development of Bayesian statistical tools able to deal with complex models. That is true for both toxicity risk assessment and therapeutic drug development.

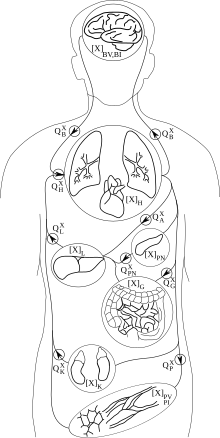
PBPK models try to rely a priori on the anatomical and physiological structure of the body, and to a certain extent, on biochemistry. They are usually multi-compartment models, with compartments corresponding to predefined organs or tissues, with interconnections corresponding to blood or lymph flows (more rarely to diffusions). A system of differential equations for concentration or quantity of substance on each compartment can be written, and its parameters represent blood flows, pulmonary ventilation rate, organ volumes etc., for which information is available in scientific publications. Indeed, the description they make of the body is simplified and a balance needs to be struck between complexity and simplicity. Besides the advantage of allowing the recruitment of a priori information about parameter values, these models also facilitate inter-species transpositions or extrapolation from one mode of administration to another (e.g., inhalation to oral). An example of a 7-compartment PBPK model, suitable to describe the fate of many solvents in the mammalian body, is given in the Figure on the right.

History

The first pharmacokinetic model described in the scientific literature was in fact a PBPK model. It led, however, to computations intractable at that time. The focus shifted then to simpler models, for which analytical solutions could be obtained (such solutions were sums of exponential terms, which led to further simplifications.) The availability of computers and numerical integration algorithms marked a renewed interest in physiological models in the early 1970s. For substances with complex kinetics, or when inter-species extrapolations were required, simple models were insufficient and research continued on physiological models. By 2010, hundreds of scientific publications had described and used PBPK models, and at least two private companies have based their business on their expertise in this area.

Building a PBPK model

The model equations follow the principles of mass transport, fluid dynamics, and biochemistry in order to simulate the fate of a substance in the body. Compartments are usually defined by grouping organs or tissues with similar blood perfusion rate and lipid content (i.e. organs for which chemicals' concentration vs. time profiles will be similar). Ports of entry (lung, skin, intestinal tract...), ports of exit (kidney, liver...) and target organs for therapeutic effect or toxicity are often left separate. Bone can be excluded from the model if the substance of interest does not distribute to it. Connections between compartment follow physiology (e.g., blood flow in exit of the gut goes to liver, etc.)

Basic transport equations

Drug distribution into a tissue can be rate-limited by either perfusion or permeability. Perfusion-rate-limited kinetics apply when the tissue membranes present no barrier to diffusion. Blood flow, assuming that the drug is transported mainly by blood, as is often the case, is then the limiting factor to distribution in the various cells of the body. That is usually true for small lipophilic drugs. Under perfusion limitation, the instantaneous rate of entry for the quantity of drug in a compartment is simply equal to (blood) volumetric flow rate through the organ times the incoming blood concentration. In that case; for a generic compartment i, the differential equation for the quantity Qi of substance, which defines the rate of change in this quantity, is:

d Q i d t = F i ( C a r t − Q i P i V i ) {\displaystyle {dQ_{i} \over dt}=F_{i}(C_{art}-{{Q_{i}} \over {P_{i}V_{i}}})}

where Fi is blood flow (noted Q in the Figure above), Cart incoming arterial blood concentration, Pi the tissue over blood partition coefficient and Vi the volume of compartment i.

A complete set of differential equations for the 7-compartment model shown above could therefore be given by the following table:

Tissue Differential Equation
Gut d Q g d t = F g ( C a r t − Q g P g V g ) {\displaystyle {dQ_{g} \over dt}=F_{g}(C_{art}-{{Q_{g}} \over {P_{g}V_{g}}})}
Kidney d Q k d t = F k ( C a r t − Q k P k V k ) {\displaystyle {dQ_{k} \over dt}=F_{k}(C_{art}-{{Q_{k}} \over {P_{k}V_{k}}})}
Poorly-perfused tissues (muscle and skin) d Q p d t = F p ( C a r t − Q p P p V p ) {\displaystyle {dQ_{p} \over dt}=F_{p}(C_{art}-{{Q_{p}} \over {P_{p}V_{p}}})}
Brain d Q b d t = F b ( C a r t − Q b P b V b ) {\displaystyle {dQ_{b} \over dt}=F_{b}(C_{art}-{{Q_{b}} \over {P_{b}V_{b}}})}
Heart and lung d Q h d t = F h ( C a r t − Q h P h V h ) {\displaystyle {dQ_{h} \over dt}=F_{h}(C_{art}-{{Q_{h}} \over {P_{h}V_{h}}})}
Pancreas d Q p n d t = F p n ( C a r t − Q p n P p n V p n ) {\displaystyle {dQ_{pn} \over dt}=F_{pn}(C_{art}-{{Q_{pn}} \over {P_{pn}V_{pn}}})}
Liver d Q l d t = F a C a r t + F g ( Q g P g V g ) + F p n ( Q p n P p n V p n ) − ( F a + F g + F p n ) ( Q l P l V l ) {\displaystyle {dQ_{l} \over dt}=F_{a}C_{art}+F_{g}({{Q_{g}} \over {P_{g}V_{g}}})+F_{pn}({{Q_{pn}} \over {P_{pn}V_{pn}}})-(F_{a}+F_{g}+F_{pn})({{Q_{l}} \over {P_{l}V_{l}}})}

The above equations include only transport terms and do not account for inputs or outputs. Those can be modeled with specific terms, as in the following.

Modeling inputs

Modeling inputs is necessary to come up with a meaningful description of a chemical's pharmacokinetics. The following examples show how to write the corresponding equations.

Ingestion

When dealing with an oral bolus dose (e.g. ingestion of a tablet), first order absorption is a very common assumption. In that case the gut equation is augmented with an input term, with an absorption rate constant Ka:

d Q g d t = F g ( C a r t − Q g P g V g ) + K a Q i n g {\displaystyle {dQ_{g} \over dt}=F_{g}(C_{art}-{{Q_{g}} \over {P_{g}V_{g}}})+K_{a}Q_{ing}}

That requires defining an equation for the quantity ingested and present in the gut lumen:

d Q i n g d t = − K a Q i n g {\displaystyle {dQ_{ing} \over dt}=-K_{a}Q_{ing}}

In the absence of a gut compartment, input can be made directly in the liver. However, in that case local metabolism in the gut may not be correctly described. The case of approximately continuous absorption (e.g. via drinking water) can be modeled by a zero-order absorption rate (here Ring in units of mass over time):

d Q g d t = F g ( C a r t − Q g P g V g ) + R i n g {\displaystyle {dQ_{g} \over dt}=F_{g}(C_{art}-{{Q_{g}} \over {P_{g}V_{g}}})+R_{ing}}

More sophisticated gut absorption model can be used. In those models, additional compartments describe the various sections of the gut lumen and tissue. Intestinal pH, transit times and presence of active transporters can be taken into account .

Skin depot

The absorption of a chemical deposited on skin can also be modeled using first order terms. It is best in that case to separate the skin from the other tissues, to further differentiate exposed skin and non-exposed skin, and differentiate viable skin (dermis and epidermis) from the stratum corneum (the actual skin upper layer exposed). This is the approach taken in

Unexposed stratum corneum simply exchanges with the underlying viable skin by diffusion:

d Q s c u d t = K p × S s × ( 1 − f S e ) × ( Q s u P s c V s c u − C s c u ) {\displaystyle {dQ_{{sc}_{u}} \over dt}=K_{p}\times S_{s}\times (1-f_{S_{e}})\times ({Q_{s_{u}} \over {P_{sc}V_{{sc}_{u}}}}-C_{{sc}_{u}})}

where K p {\displaystyle K_{p}} is the partition coefficient, S s {\displaystyle S_{s}} is the total skin surface area, f S e {\displaystyle f_{S_{e}}} the fraction of skin surface area exposed, ...

For the viable skin unexposed:

d Q s u d t = F s ( 1 − f S e ) ( C a r t − Q s u P s V s u ) − d Q s c u d t {\displaystyle {dQ_{s_{u}} \over dt}=F_{s}(1-f_{S_{e}})(C_{art}-{{Q_{s_{u}}} \over {P_{s}V_{s_{u}}}})-{dQ_{{sc}_{u}} \over dt}}

For the skin stratum corneum exposed:

d Q s c e d t = K p × S s × f S e × ( Q s e P s c V s c e − C s c e ) {\displaystyle {dQ_{{sc}_{e}} \over dt}=K_{p}\times S_{s}\times f_{S_{e}}\times ({Q_{s_{e}} \over {P_{sc}V_{{sc}_{e}}}}-C_{{sc}_{e}})}

for the viable skin exposed:

d Q s e d t = F s f S e ( C a r t − Q s e P s V s e ) − d Q s c e d t {\displaystyle {dQ_{s_{e}} \over dt}=F_{s}f_{S_{e}}(C_{art}-{{Q_{s_{e}}} \over {P_{s}V_{s_{e}}}})-{dQ_{{sc}_{e}} \over dt}}

dt(QSkin_u) and dt(QSkin_e) feed from arterial blood and back to venous blood.

More complex diffusion models have been published .

Intra-venous injection

Intravenous injection is a common clinical route of administration. (to be completed)

Inhalation

Inhalation occurs through the lung and is hardly dissociable from exhalation (to be completed)

Modelling metabolism

There are several ways metabolism can be modeled. For some models, a linear excretion rate is preferred. This can be accomplished with a simple differential equation. Otherwise a Michaelis-Menten equation, as follows, is generally appropriate for a more accurate result.

v = d [ P ] d t = V max [ S ] K m + [ S ] {\displaystyle v={\frac {d}{dt}}={\frac {V_{\max }{}}{K_{m}+}}} .

Uses of PBPK modeling

Simulated drug plasma concentration over time curves following IV infusion and multiple oral doses. The drug has an elimination half-life of 4 hours, and an apparent volume of distribution of 10 liters.
Pharmacokinetic model of drugs entering a tumor. (A) Schematic illustration of a tumor vessel illustrating loss of smooth muscle cells, local degradation of the extracellular matrix, and increased permeability of the endothelium. (B) Illustration of the pharmacokinetic model taking into account the EPR effect. The rate constants kp and kd describe exchange with the peripheral volume. The rate constants kepr and kb describe extravasation from circulation into the tumor, and intravasation back into the circulation, respectively. The rate constant kel represents clearance by the kidneys, MPS, and any other non-tumor elimination processes, such that when kb = 0, k10 = kepr + kel where kel is the elimination rate constant. (C) Standard two compartment model with central and peripheral compartments. c1 and c2 represent the drug concentration in blood (central compartment) and normal tissue (peripheral compartment), respectively. The first order rate constant k10 describes all elimination pathways, including clearance by the kidneys, uptake by the MPS, and tumor accumulation. The first order rate constants k12 and k21 describe exchange between the two compartments. Note that kp = k12, kd = k21. (D) Two compartment model defined in terms of the drug amount, where Nbl is the amount of drug in blood (mg), and Np is the amount in peripheral tissue (mg). (E) Three compartment model with the addition of a tumor “compartment” where Nt is the amount of drug in the tumor. Exchange with the tumor is described by the rate constants kepr and kb, respectively. The rate constant kel describes elimination pathways including clearance by the kidneys and uptake by the MPS, but does not include tumor accumulation.

PBPK models are compartmental models like many others, but they have a few advantages over so-called "classical" pharmacokinetic models, which are less grounded in physiology. PBPK models can first be used to abstract and eventually reconcile disparate data (from physicochemical or biochemical experiments, in vitro or in vivo pharmacological or toxicological experiments, etc.) They give also access to internal body concentrations of chemicals or their metabolites, and in particular at the site of their effects, be it therapeutic or toxic. Finally they also help interpolation and extrapolation of knowledge between:

  • Doses: e.g., from the high concentrations typically used in laboratory experiments to those found in the environment
  • Exposure duration: e.g., from continuous to discontinuous, or single to multiple exposures
  • Routes of administration: e.g., from inhalation exposures to ingestion
  • Species: e.g., transpositions from rodents to human, prior to giving a drug for the first time to subjects of a clinical trial, or when experiments on humans are deemed unethical, such as when the compound is toxic without therapeutic benefit
  • Individuals: e.g., from males to females, from adults to children, from non-pregnant women to pregnant
  • From in vitro to in vivo.

Some of these extrapolations are "parametric" : only changes in input or parameter values are needed to achieve the extrapolation (this is usually the case for dose and time extrapolations). Others are "nonparametric" in the sense that a change in the model structure itself is needed (e.g., when extrapolating to a pregnant female, equations for the foetus should be added).

Owing to the mechanistic basis of PBPK models, another potential use of PBPK modeling is hypothesis testing. For example, if a drug compound showed lower-than-expected oral bioavailability, various model structures (i.e., hypotheses) and parameter values can be evaluated to determine which models and/or parameters provide the best fit to the observed data. If the hypothesis that metabolism in the intestines was responsibility for the low bioavailability yielded the best fit, then the PBPK modeling results support this hypothesis over the other hypotheses evaluated.

As such, PBPK modeling can be used, inter alia, to evaluate the involvement of carrier-mediated transport, clearance saturation, enterohepatic recirculation of the parent compound, extra-hepatic/extra-gut elimination; higher in vivo solubility than predicted in vitro; drug-induced gastric emptying delays; gut loss and regional variation in gut absorption.

Limits and extensions of PBPK modeling

Each type of modeling technique has its strengths and limitations. PBPK modeling is no exception. One limitation is the potential for a large number of parameters, some of which may be correlated. This can lead to the issues of parameter identifiability and redundancy. However, it is possible (and commonly done) to model explicitly the correlations between parameters (for example, the non-linear relationships between age, body-mass, organ volumes and blood flows).

After numerical values are assigned to each PBPK model parameter, specialized or general computer software is typically used to numerically integrate a set of ordinary differential equations like those described above, in order to calculate the numerical value of each compartment at specified values of time (see Software). However, if such equations involve only linear functions of each compartmental value, or under limiting conditions (e.g., when input values remain very small) that guarantee such linearity is closely approximated, such equations may be solved analytically to yield explicit equations (or, under those limiting conditions, very accurate approximations) for the time-weighted average (TWA) value of each compartment as a function of the TWA value of each specified input (see, e.g.,).

PBPK models can rely on chemical property prediction models (QSAR models or predictive chemistry models) on one hand. For example, QSAR models can be used to estimate partition coefficients. They also extend into, but are not destined to supplant, systems biology models of metabolic pathways. They are also parallel to physiome models, but do not aim at modelling physiological functions beyond fluid circulation in detail. In fact the above four types of models can reinforce each other when integrated.

References

  1. Gelman, A.; Bois, F.Y.; Jiang, J. (1996). "Physiological pharmacokinetic analysis using population modeling and informative prior distributions". Journal of the American Statistical Association. 91 (436): 1400–1412. CiteSeerX 10.1.1.44.2288. doi:10.1080/01621459.1996.10476708.
  2. Teorell, T. (1937). "Kinetics of distribution of substances administered to the body". Archives Internationales de Pharmacodynamie et de Thérapie. 57: 205–240.
  3. Gibaldi M., and Perrier D. (1982). Pharmacokinetics, , Second Edition, revised and expanded ed. New-York: Marcel Dekker.
  4. Bischoff, K.B.; Dedrick, R.L.; Zaharko, D.S.; Longstreth, J.A. (1971). "Methotrexate pharmacokinetics". Journal of Pharmaceutical Sciences. 60 (8): 1128–1133. doi:10.1002/jps.2600600803. PMID 5127083.
  5. Dedrick, R.L.; Forrester, D.D.; Cannon, J.N.; El Dareer, S.M.; Mellett, L.B. (1973). "Pharmacokinetics of 1-beta-D-arabinofuranosylcytosine (ARA-C) deamination in several species". Biochemical Pharmacology. 22 (19): 2405–2417. doi:10.1016/0006-2952(73)90342-0. PMID 4200888.
  6. Gerlowski, L.E.; Jain, R.K. (1983). "Physiologically based pharmacokinetic modeling: principles and applications". Journal of Pharmaceutical Sciences. 72 (10): 1103–1127. doi:10.1002/jps.2600721003. PMID 6358460.
  7. Droz, P.O.; Guillemin, M. P. (1983). "Human styrene exposure - V. Development of a model for biological monitoring". International Archives of Occupational and Environmental Health. 53 (1): 19–36. doi:10.1007/bf00406174. PMID 6654499. S2CID 21135553.
  8. Lutz, R.J.; Dedrick, R.L.; Tuey, D.; Sipes, G.; Anderson, M.W.; Matthews, H.B. (1984). "Comparison of the pharmacokinetics of several polychlorinated biphenyls in mouse, rat, dog, and monkey by means of a physiological pharmacokinetic model". Drug Metabolism and Disposition. 12 (5): 527–535. PMID 6149901.
  9. Campbell JL Jr, Clewell RA, Gentry PR, Andersen ME, Clewell HJ 3rd (2012). "Physiologically based pharmacokinetic/toxicokinetic modeling". Computational Toxicology. Methods in Molecular Biology. Vol. 929. pp. 439–499. doi:10.1007/978-1-62703-050-2_18. ISBN 978-1-62703-049-6. PMID 23007440.
  10. Jeong, Yoo-Seong; Yim, Chang-Soon; Ryu, Heon-Min; Noh, Chi-Kyoung; Song, Yoo-Kyung; Chung, Suk-Jae (2017). "Estimation of the minimum permeability coefficient in rats for perfusion-limited tissue distribution in whole-body physiologically-based pharmacokinetics". European Journal of Pharmaceutics and Biopharmaceutics. 115: 1–17. doi:10.1016/j.ejpb.2017.01.026. PMID 28215648. S2CID 3455193.
  11. Espié, Pascal; Tytgat, Dominique; Sargentini-Maier, Maria-Laura; Poggesi, Italo; Watelet, Jean-Baptiste (2009). "Physiologically based pharmacokinetics (PBPK)". Drug Metabolism Reviews. 41 (3): 391–407. doi:10.1080/10837450902891360. ISSN 1097-9883. PMID 19601719. S2CID 20219523.
  12. Darwich, AS; Pade D; Ammori BJ; Jamei M; Ashcroft DM; Rostami-Hodjegan A (2012). "A mechanistic pharmacokinetic model to assess modified oral drug bioavailability post bariatric surgery in morbidly obese patients: interplay between CYP3A gut wall metabolism, permeability and dissolution". Journal of Pharmacy and Pharmacology. 64 (7): 1008–1024. doi:10.1111/j.2042-7158.2012.01538.x. PMID 22686346. S2CID 46066754.
  13.  This article incorporates D. Wong, Mao Ye, Martin B. Ulmschneider, Peter C. Searson text available under the CC BY 4.0 license.
  14. Bouvier d'Yvoire, M.; Prieto P.; Blaauboer B.J.; Bois F.; Boobis A.; Brochot C.; Coecke S.; Freidig A.; Gundert-Remy U.; Hartung T.; Jacobs M. N.; Lavé T.; Leahy D.E.; Lennernäs H.; Loizou G.D.; Meek B.; Pease C.; Rowland M.; Spendiff M.; Yang J.; Zeilmaker M. (2007). "Physiologically-based kinetic modelling (PBK modelling): meeting the 3Rs agenda - The report and recommendations of ECVAM Workshop 63a". Alternatives to Laboratory Animals. 35 (6): 661–671. doi:10.1177/026119290703500606. PMID 18186671. S2CID 1247463.
  15. Peters, SA (2008). "Evaluation of a generic physiologically based pharmacokinetic model for lineshape analysis". Clin Pharmacokinet. 47 (4): 261–75. doi:10.2165/00003088-200847040-00004. PMID 18336055. S2CID 10598918.
  16. Bogen, K.T. (1988). "Pharmacokinetics for regulatory risk analysis: The case of trichloroethylene". Regulatory Toxicology and Pharmacology. 8 (4): 447–466. doi:10.1016/0273-2300(88)90045-1. PMID 3222486.
  17. Bogen, K.T.; Hall, L.C. (1989). "Pharmacokinetics for regulatory risk analysis: The case of 1,1,1-trichloroethane (methyl chloroform)". Regulatory Toxicology and Pharmacology. 10 (1): 26–50. doi:10.1016/0273-2300(89)90011-1. PMID 2672126.
  18. Bois, F.Y. (2009). "Physiologically-based modelling and prediction of drug interactions". Basic & Clinical Pharmacology & Toxicology. 106 (3): 154–161. doi:10.1111/j.1742-7843.2009.00488.x. PMID 19912164.

Further references:

Forums

  • Ecotoxmodels is a website on mathematical models in ecotoxicology.

Software

Dedicated software:

General software:

Categories: