Misplaced Pages

Piecewise function

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
(Redirected from Piecewise functions) Function defined by multiple sub-functions "Piecewise" redirects here. For other uses, see Piecewise property.
This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.
Find sources: "Piecewise function" – news · newspapers · books · scholar · JSTOR (March 2017) (Learn how and when to remove this message)
Plot of the piecewise linear function f ( x ) = { − 3 − x if x ≤ − 3 x + 3 if − 3 ≤ x ≤ 0 3 − 2 x if 0 ≤ x ≤ 3 0.5 x − 4.5 if 3 ≤ x {\displaystyle f(x)=\left\{{\begin{array}{lll}-3-x&{\text{if}}&x\leq -3\\x+3&{\text{if}}&-3\leq x\leq 0\\3-2x&{\text{if}}&0\leq x\leq 3\\0.5x-4.5&{\text{if}}&3\leq x\\\end{array}}\right.}

In mathematics, a piecewise function (also called a piecewise-defined function, a hybrid function, or a function defined by cases) is a function whose domain is partitioned into several intervals ("subdomains") on which the function may be defined differently. Piecewise definition is actually a way of specifying the function, rather than a characteristic of the resulting function itself.

Terms like piecewise linear, piecewise smooth, piecewise continuous, and others are very common. The meaning of a function being piecewise P {\displaystyle P} , for a property P {\displaystyle P} is roughly that the domain of the function can be partitioned into pieces on which the property P {\displaystyle P} holds, but is used slightly differently by different authors. Sometimes the term is used in a more global sense involving triangulations; see Piecewise linear manifold.

Notation and interpretation

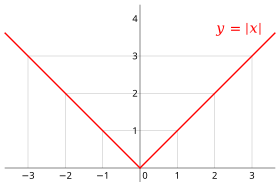
Graph of the absolute value function, y = | x | {\displaystyle y=|x|}

Piecewise functions can be defined using the common functional notation, where the body of the function is an array of functions and associated subdomains. A semicolon or comma may follow the subfunction or subdomain columns. The if {\displaystyle {\text{if}}} or for {\displaystyle {\text{for}}} is rarely omitted at the start of the right column.

The subdomains together must cover the whole domain; often it is also required that they are pairwise disjoint, i.e. form a partition of the domain. In order for the overall function to be called "piecewise", the subdomains are usually required to be intervals (some may be degenerated intervals, i.e. single points or unbounded intervals). For bounded intervals, the number of subdomains is required to be finite, for unbounded intervals it is often only required to be locally finite. For example, consider the piecewise definition of the absolute value function: | x | = { − x , if  x < 0 + x , if  x ≥ 0. {\displaystyle |x|={\begin{cases}-x,&{\text{if }}x<0\\+x,&{\text{if }}x\geq 0.\end{cases}}} For all values of x {\displaystyle x} less than zero, the first sub-function ( − x {\displaystyle -x} ) is used, which negates the sign of the input value, making negative numbers positive. For all values of x {\displaystyle x} greater than or equal to zero, the second sub-function ( x {\displaystyle x} ) is used, which evaluates trivially to the input value itself.

The following table documents the absolute value function at certain values of x {\displaystyle x} :

x f(x) Sub-function used
−3 3 − x {\displaystyle -x}
−0.1 0.1 − x {\displaystyle -x}
0 0 x {\displaystyle x}
1/2 1/2 x {\displaystyle x}
5 5 x {\displaystyle x}

In order to evaluate a piecewise-defined function at a given input value, the appropriate subdomain needs to be chosen in order to select the correct sub-function—and produce the correct output value.

Examples

  • A step function or piecewise constant function, composed of constant sub-functions
  • Piecewise linear function, composed of linear sub-functions
  • Broken power law, a function composed of power-law sub-functions
  • Spline, a function composed of polynomial sub-functions, often constrained to be smooth at the joints between pieces
  • PDIFF
  • f ( x ) = { exp ⁡ ( − 1 1 − x 2 ) , x ∈ ( − 1 , 1 ) 0 , otherwise {\displaystyle f(x)={\begin{cases}\exp \left(-{\frac {1}{1-x^{2}}}\right),&x\in (-1,1)\\0,&{\text{otherwise}}\end{cases}}}
    and some other common Bump functions. These are infinitely differentiable, but analyticity holds only piecewise.

Continuity and differentiability of piecewise-defined functions

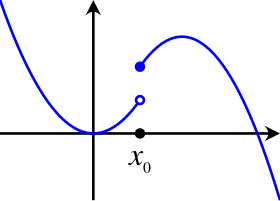
Plot of the piecewise-quadratic function f ( x ) = { x 2 if x < 0.707 1.5 − ( x − 1.414 ) 2 if 0.707 ≤ x {\displaystyle f(x)=\left\{{\begin{array}{lll}x^{2}&{\text{if}}&x<0.707\\1.5-(x-1.414)^{2}&{\text{if}}&0.707\leq x\\\end{array}}\right.} Its only discontinuity is at x 0 = 0.707 {\displaystyle x_{0}=0.707} .

A piecewise-defined function is continuous on a given interval in its domain if the following conditions are met:

  • its sub-functions are continuous on the corresponding intervals (subdomains),
  • there is no discontinuity at an endpoint of any subdomain within that interval.

The pictured function, for example, is piecewise-continuous throughout its subdomains, but is not continuous on the entire domain, as it contains a jump discontinuity at x 0 {\displaystyle x_{0}} . The filled circle indicates that the value of the right sub-function is used in this position.

For a piecewise-defined function to be differentiable on a given interval in its domain, the following conditions have to fulfilled in addition to those for continuity above:

  • its sub-functions are differentiable on the corresponding open intervals,
  • the one-sided derivatives exist at all intervals' endpoints,
  • at the points where two subintervals touch, the corresponding one-sided derivatives of the two neighboring subintervals coincide.

Some sources only examine the function definition, while others acknowledge the property iff the function admits a partition into a piecewise definition that meets the conditions.

Applications

In applied mathematical analysis, "piecewise-regular" functions have been found to be consistent with many models of the human visual system, where images are perceived at a first stage as consisting of smooth regions separated by edges (as in a cartoon); a cartoon-like function is a C function, smooth except for the existence of discontinuity curves. In particular, shearlets have been used as a representation system to provide sparse approximations of this model class in 2D and 3D.

Piecewise defined functions are also commonly used for interpolation, such as in nearest-neighbor interpolation.

See also

References

  1. "Piecewise Functions". www.mathsisfun.com. Retrieved 2020-08-24.
  2. ^ Weisstein, Eric W. "Piecewise Function". mathworld.wolfram.com. Retrieved 2020-08-24.
  3. "Piecewise functions". brilliant.org. Retrieved 2020-09-29.
  4. ^ Weisstein, Eric W. "Piecewise Function". mathworld.wolfram.com. Retrieved 2024-07-20.
  5. A feasible weaker requirement is that all definitions agree on intersecting subdomains.
  6. "Differentiability of Piecewise Defined Functions – AP Central | College Board". apcentral.collegeboard.org. Retrieved 2024-08-26.
  7. S. M. Nikolsky (1977). A Course Of Mathematical Analysis Vol 1. p. 178.
  8. Sofronidis, Nikolaos Efstathiou (2005). "The set of continuous piecewise differentiable functions". Real Analysis Exchange. 31 (1): 13–22. doi:10.14321/realanalexch.31.1.0013. ISSN 0147-1937.
  9. Kutyniok, Gitta; Labate, Demetrio (2012). "Introduction to shearlets" (PDF). Shearlets. Birkhäuser: 1–38. Here: p.8
  10. Kutyniok, Gitta; Lim, Wang-Q (2011). "Compactly supported shearlets are optimally sparse". Journal of Approximation Theory. 163 (11): 1564–1589. arXiv:1002.2661. doi:10.1016/j.jat.2011.06.005.
Category: