Misplaced Pages

Plücker's conoid

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
Right conoid ruled surface
Figure 1. Plücker's conoid with n = 2.
Figure 2. Plücker's conoid with n = 3.
Figure 3. Plücker's conoid with n = 4.
This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (September 2022) (Learn how and when to remove this message)

In geometry, Plücker's conoid is a ruled surface named after the German mathematician Julius Plücker. It is also called a conical wedge or cylindroid; however, the latter name is ambiguous, as "cylindroid" may also refer to an elliptic cylinder.

Plücker's conoid is the surface defined by the function of two variables:

z = 2 x y x 2 + y 2 . {\displaystyle z={\frac {2xy}{x^{2}+y^{2}}}.}

This function has an essential singularity at the origin.

By using cylindrical coordinates in space, we can write the above function into parametric equations

x = v cos ⁡ u , y = v sin ⁡ u , z = sin ⁡ 2 u . {\displaystyle x=v\cos u,\quad y=v\sin u,\quad z=\sin 2u.}

Thus Plücker's conoid is a right conoid, which can be obtained by rotating a horizontal line about the z-axis with the oscillatory motion (with period 2π) along the segment of the axis (Figure 4).

A generalization of Plücker's conoid is given by the parametric equations

x = v cos ⁡ u , y = v sin ⁡ u , z = sin ⁡ n u . {\displaystyle x=v\cos u,\quad y=v\sin u,\quad z=\sin nu.}

where n denotes the number of folds in the surface. The difference is that the period of the oscillatory motion along the z-axis is ⁠2π/n⁠. (Figure 5 for n = 3)

Figure 4. Plücker's conoid with n = 2.
Figure 5. Plücker's conoid with n = 3
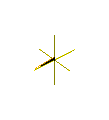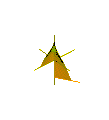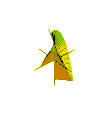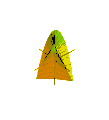  • Animation of Plucker's conoid with n = 2 Animation of Plucker's conoid with n = 2
  • Plucker's conoid with n = 2 Plucker's conoid with n = 2
  • Plucker's conoid with n = 3 Plucker's conoid with n = 3
  • Animation of Plucker's conoid with n = 2 Animation of Plucker's conoid with n = 2
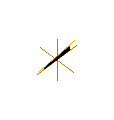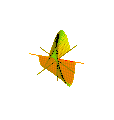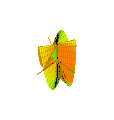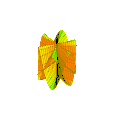  • Animation of Plucker's conoid with n = 3 Animation of Plucker's conoid with n = 3
  • Plucker's conoid with n = 4 Plucker's conoid with n = 4

See also

References

  • A. Gray, E. Abbena, S. Salamon, Modern differential geometry of curves and surfaces with Mathematica, 3rd ed. Boca Raton, Florida:CRC Press, 2006. (ISBN 978-1-58488-448-4)
  • Vladimir Y. Rovenskii, Geometry of curves and surfaces with MAPLE (ISBN 978-0-8176-4074-3)

External links


Stub icon

This algebraic geometry–related article is a stub. You can help Misplaced Pages by expanding it.

Categories: