Misplaced Pages

The Playfair cipher or Playfair square or Wheatstone–Playfair cipher is a manual symmetric encryption technique and was the first literal digram substitution cipher. The scheme was invented in 1854 by Charles Wheatstone, but bears the name of Lord Playfair for promoting its use.

The technique encrypts pairs of letters (bigrams or digrams), instead of single letters as in the simple substitution cipher and rather more complex Vigenère cipher systems then in use. The Playfair cipher is thus significantly harder to break since the frequency analysis used for simple substitution ciphers does not work with it. The frequency analysis of bigrams is possible, but considerably more difficult. With 600 possible bigrams rather than the 26 possible monograms (single symbols, usually letters in this context), a considerably larger cipher text is required in order to be useful.

History

Playfair cipher was the first cipher to encrypt pairs of letters in cryptologic history. Wheatstone invented the cipher for secrecy in telegraphy, but it carries the name of his friend Lord Playfair, first Baron Playfair of St. Andrews, who promoted its use. The first recorded description of the Playfair cipher was in a document signed by Wheatstone on 26 March 1854.

It was initially rejected by the British Foreign Office when it was developed because of its perceived complexity. Wheatstone offered to demonstrate that three out of four boys in a nearby school could learn to use it in 15 minutes, but the Under Secretary of the Foreign Office responded, "That is very possible, but you could never teach it to attachés."

It was however later used for tactical purposes by British forces in the Second Boer War and in World War I and for the same purpose by the British and Australians during World War II. This was because Playfair is reasonably fast to use and requires no special equipment - just a pencil and some paper. A typical scenario for Playfair use was to protect important but non-critical secrets during actual combat e.g. the fact that an artillery barrage of smoke shells would commence within 30 minutes to cover soldiers' advance towards the next objective. By the time enemy cryptanalysts could decode such messages hours later, such information would be useless to them because it was no longer relevant.

During World War II, the Government of New Zealand used it for communication among New Zealand, the Chatham Islands, and the coastwatchers in the Pacific Islands. Coastwatchers established by Royal Australian Navy Intelligence also used this cipher.

Superseded

Playfair is no longer used by military forces because of known insecurities and of the advent of automated encryption devices. This cipher is regarded as insecure since before World War I.

The first published solution of the Playfair cipher was described in a 19-page pamphlet by Lieutenant Joseph O. Mauborgne, published in 1914. William Friedman described it in 1942 as providing very little security.

Description

The Playfair cipher uses a 5 * 5 table containing a key word or phrase. Memorization of the keyword and 4 simple rules was all that was required to create the 5 by 5 table and use the cipher.

To generate the key table, one would first fill in the spaces in the table (a modified Polybius square) with the letters of the keyword (dropping any duplicate letters), then fill the remaining spaces with the rest of the letters of the alphabet in order (usually omitting "J" or "Q" to reduce the alphabet to fit; other versions put both "I" and "J" in the same space). The key can be written in the top rows of the table, from left to right, or in some other pattern, such as a spiral beginning in the upper-left-hand corner and ending in the center. The keyword together with the conventions for filling in the 5 by 5 table constitute the cipher key.

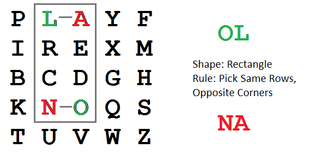
To encrypt a message, one would break the message into digrams (groups of 2 letters) such that, for example, "HelloWorld" becomes "HE LL OW OR LD". These digrams will be substituted using the key table. Since encryption requires pairs of letters, messages with an odd number of characters usually append an uncommon letter, such as "X", to complete the final digram. The two letters of the digram are considered opposite corners of a rectangle in the key table. To perform the substitution, apply the following 4 rules, in order, to each pair of letters in the plaintext:

1. If both letters are the same (or only one letter is left), add an "X" after the first letter. Encrypt the new pair and continue. Some variants of Playfair use "Q" instead of "X", but any letter, itself uncommon as a repeated pair, will do.
2. If the letters appear on the same row of your table, replace them with the letters to their immediate right respectively (wrapping around to the left side of the row if a letter in the original pair was on the right side of the row).
3. If the letters appear on the same column of your table, replace them with the letters immediately below respectively (wrapping around to the top side of the column if a letter in the original pair was on the bottom side of the column).
4. If the letters are not on the same row or column, replace them with the letters on the same row respectively but at the other pair of corners of the rectangle defined by the original pair. The order is important – the first letter of the encrypted pair is the one that lies on the same row as the first letter of the plaintext pair.

To decrypt, use the inverse (opposite) of the two shift rules, selecting the letter to the left or upwards as appropriate. The last rule remains unchanged, as the transformation switches the selected letters of the rectangle to the opposite diagonal, and a repeat of the transformation returns the selection to its original state. The first rule can only be reversed by dropping any extra instances of the chosen insert letter — generally "X"s or "Q"s — that do not make sense in the final message when finished.

There are several minor variations of the original Playfair cipher.

Example

Using "playfair example" as the key (assuming that I and J are interchangeable), the table becomes (omitted letters in red):

The first step of encrypting the message "hide the gold in the tree stump" is to convert it to the pairs of letters "HI DE TH EG OL DI NT HE TR EX ES TU MP" (with the null "X" used to separate the repeated "E"s). Then:

1. The pair HI forms a rectangle, replace it with BM
2. The pair DE is in a column, replace it with OD
3. The pair TH forms a rectangle, replace it with ZB
4. The pair EG forms a rectangle, replace it with XD
5. The pair OL forms a rectangle, replace it with NA
6. The pair DI forms a rectangle, replace it with BE
7. The pair NT forms a rectangle, replace it with KU
8. The pair HE forms a rectangle, replace it with DM
9. The pair TR forms a rectangle, replace it with UI
10. The pair EX (X inserted to split EE) is in a row, replace it with XM
11. The pair ES forms a rectangle, replace it with MO
12. The pair TU is in a row, replace it with UV
13. The pair MP forms a rectangle, replace it with IF

Thus the message "hide the gold in the tree stump" becomes "BM OD ZB XD NA BE KU DM UI XM MO UV IF", which may be restructured as "BMODZ BXDNA BEKUD MUIXM MOUVI F" for ease of reading the cipher text.

Clarification with picture

Assume one wants to encrypt the digram OR. There are five general cases:

* * * * *
* O Y R Z
* * * * *
* * * * *
* * * * *

* * O * *
* * B * *
* * * * *
* * R * *
* * Y * *

Z * * O *
* * * * *
* * * * *
R * * X *
* * * * *

* * * * *
* * * * *
* O R W *
* * * * *
* * * * *

* * * * *
* * R * *
* * O * *
* * I * *
* * * * *

Cryptanalysis

Like most classical ciphers, the Playfair cipher can be easily cracked if there is enough text. Obtaining the key is relatively straightforward if both plaintext and ciphertext are known. When only the ciphertext is known, brute force cryptanalysis of the cipher involves searching through the key space for matches between the frequency of occurrence of digrams (pairs of letters) and the known frequency of occurrence of digrams in the assumed language of the original message.

Cryptanalysis of Playfair is similar to that of four-square and two-square ciphers, though the relative simplicity of the Playfair system makes identifying candidate plaintext strings easier. Most notably, a Playfair digraph and its reverse (e.g. AB and BA) will decrypt to the same letter pattern in the plaintext (e.g. RE and ER). In English, there are many words which contain these reversed digraphs such as REceivER and DEpartED. Identifying nearby reversed digraphs in the ciphertext and matching the pattern to a list of known plaintext words containing the pattern is an easy way to generate possible plaintext strings with which to begin constructing the key.

A different approach to tackling a Playfair cipher is the shotgun hill climbing method. This starts with a random square of letters. Then minor changes are introduced (i.e. switching letters, rows, or reflecting the entire square) to see if the candidate plaintext is more like standard plaintext than before the change (perhaps by comparing the digrams to a known frequency chart). If the new square is deemed to be an improvement, then it is adopted and then further mutated to find an even better candidate. Eventually, the plaintext or something very close is found to achieve a maximal score by whatever grading method is chosen. This is obviously beyond the range of typical human patience, but computers can adopt this algorithm to crack Playfair ciphers with a relatively small amount of text.

Another aspect of Playfair that separates it from four-square and two-square ciphers is the fact that it will never contain a double-letter digram, e.g. EE. If there are no double letter digrams in the ciphertext and the length of the message is long enough to make this statistically significant, it is very likely that the method of encryption is Playfair.

A good tutorial on reconstructing the key for a Playfair cipher can be found in chapter 7, "Solution to Polygraphic Substitution Systems," of Field Manual 34-40-2, produced by the United States Army. Another cryptanalysis of a Playfair cipher can be found in Chapter XXI of Helen Fouché Gaines' Cryptanalysis / a study of ciphers and their solutions.

A detailed cryptanalysis of Playfair is undertaken in chapter 28 of Dorothy L. Sayers' mystery novel Have His Carcase. In this story, a Playfair message is demonstrated to be cryptographically weak, as the detective is able to solve for the entire key making only a few guesses as to the formatting of the message (in this case, that the message starts with the name of a city and then a date). Sayers' book includes a detailed description of the mechanics of Playfair encryption, as well as a step-by-step account of manual cryptanalysis.

The German Army, Air Force and Police used the Double Playfair cipher as a medium-grade cipher in WWII, based on the British Playfair cipher they had broken early in WWI. They adapted it by introducing a second square from which the second letter of each bigram was selected, and dispensed with the keyword, placing the letters in random order. But with the German fondness for pro forma messages, they were broken at Bletchley Park. Messages were preceded by a sequential number, and numbers were spelled out. As the German numbers 1 (eins) to twelve (zwölf) contain all but eight of the letters in the Double Playfair squares, pro forma traffic was relatively easy to break (Smith, page 74-75)

Use in modern crosswords

Advanced thematic cryptic crosswords like The Listener Crossword (published in the Saturday edition of the British newspaper The Times) occasionally incorporate Playfair ciphers. Normally between four and six answers have to be entered into the grid in code, and the Playfair keyphrase is thematically significant to the final solution.

The cipher lends itself well to crossword puzzles, because the plaintext is found by solving one set of clues, while the ciphertext is found by solving others. Solvers can then construct the key table by pairing the digrams (it is sometimes possible to guess the keyword, but never necessary).

Use of the Playfair cipher is generally explained as part of the preamble to the crossword. This levels the playing field for those solvers who have not come across the cipher previously. But the way the cipher is used is always the same. The 25-letter alphabet used always contains Q and has I and J coinciding. The key table is always filled row by row.

In popular culture

• The novel Have His Carcase by Dorothy L. Sayers gives a blow-by-blow account of the cracking of a Playfair cipher.
• The World War 2 thriller The Trojan Horse by Hammond Innes conceals the formula for a new high-strength metal alloy using the Playfair cipher.
• In the film National Treasure: Book of Secrets, a treasure hunt clue is encoded as a Playfair cipher.
• In the audio book Rogue Angel : God of Thunder, a Playfair cipher clue is used to send Anja Creed to Venice.
• In the novel York: The Map of Stars (part three of a trilogy for children) by Laura Ruby, a clue to solving the Morningstarr cipher is encrypted using the Playfair cipher.
• The Playfair cipher serves as a plot device in a season 2 episode of the 2019 Batwoman (TV series).
• In the novel S. (Dorst novel), a Playfair cipher is discovered in the footnotes of the story.

See also

• Topics in cryptography

Notes

1. No duplicate letters are allowed, and one letter is omitted (Q) or combined (I/J), so the calculation is 600 = 25×24.
2. The Codebreakers (1996) David Kahn, Scribner Books from Simon & Schuster
3. Christensen, Chris (2006). "Polygraphic Ciphers" (PDF). Northern Kentucky University, Chris Christensen. Retrieved January 9, 2018.
4. ^ Kahn, David (1996). The Codebreakers: The comprehensive history of secret communi cation from ancient times to the internet. Scribner. ISBN 978-0684831305.
5. ^ Klima, Rick (2018). "Secret Codes Through World War II" (PDF). Appalachian State University, Dr. Rick Klima. Archived from the original (PDF) on 2017-10-13. Retrieved 2018-01-09.
6. Reid, Thomas Wemyss (1899). Memoirs and Correspondence of Lyon Playfair: First Lord Playfair of St. Andrews ... Harper & Brothers. pp. 158–159.
7. Lord, Walter (2012). Lonely Vigil: Coastwatchers of the Solomons. Open Road Media. Kindle Edition. p. 6.
8. "A History of Communications Security in New Zealand By Eric Mogon", Chapter 8
9. "The History of Information Assurance (IA)". Government Communications Security Bureau. New Zealand Government. Archived from the original on 2011-11-12. Retrieved 2011-12-24.
10. Lord, Walter (2012). Lonely Vigil: Coastwatchers of the Solomons. Open Road Media. Kindle Edition. p. 6.
11. Mauborgne, Joseph Oswald (1914). An Advanced Problem in Cryptography and Its Solution. Fort Leavenwoth, Kansas: Army Service Schools Press.
12. Friedman, William (June 1942). American Army Field Codes In the American Expeditionary Forces During The First World War (PDF). U.S. War Department. p. 4.
13. Gaines 1956, p. 201
14. Gaines 1956, p. 201
15. Gaines 1956, pp. 198–207
16. Currer-Briggs, Noel (1987). "Some of ultra's poor relations in Algeria, Tunisia, Sicily and Italy". Intelligence and National Security. 2 (2): 274–290. doi:10.1080/02684528708431890.
17. Listener crossword database

References

• Gaines, Helen Fouché (1956) , Cryptanalysis / a study of ciphers and their solutions, Dover, ISBN 0-486-20097-3
• Smith, Michael Station X: The Codebreakers of Bletchley Park (1998, Channel 4 Books/Macmillan, London) ISBN 0-7522-2189-2
• Kahn, David (1996), The Codebreakers: The Comprehensive History of Secret Communication from Ancient Times to the Internet, Scribner, ISBN 978-0684831305

External links

• Online encrypting and decrypting Playfair with JavaScript
• Extract from some lecture notes on ciphers – Digraphic Ciphers: Playfair
• Playfair Cipher
• Cross platform implementation of Playfair cipher
• Javascript implementation of the Playfair cipher
• Python and streamlit implementation of Playfair cipher

• Classical ciphers
• English inventions