Misplaced Pages

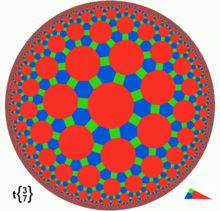
In geometry, the Poincaré disk model, also called the conformal disk model, is a model of 2-dimensional hyperbolic geometry in which all points are inside the unit disk, and straight lines are either circular arcs contained within the disk that are orthogonal to the unit circle or diameters of the unit circle.

The group of orientation preserving isometries of the disk model is given by the projective special unitary group PSU(1,1), the quotient of the special unitary group SU(1,1) by its center {I, −I}.

Along with the Klein model and the Poincaré half-space model, it was proposed by Eugenio Beltrami who used these models to show that hyperbolic geometry was equiconsistent with Euclidean geometry. It is named after Henri Poincaré, because his rediscovery of this representation fourteen years later became better known than the original work of Beltrami.

The Poincaré ball model is the similar model for 3 or n-dimensional hyperbolic geometry in which the points of the geometry are in the n-dimensional unit ball.

History

The disk model was first described by Bernhard Riemann in an 1854 lecture (published 1868), which inspired an 1868 paper by Eugenio Beltrami. Henri Poincaré employed it in his 1882 treatment of hyperbolic, parabolic and elliptic functions, but it became widely known following Poincaré's presentation in his 1905 philosophical treatise, Science and Hypothesis. There he describes a world, now known as the Poincaré disk, in which space was Euclidean, but which appeared to its inhabitants to satisfy the axioms of hyperbolic geometry:

"Suppose, for example, a world enclosed in a large sphere and subject to the following laws: The temperature is not uniform; it is greatest at their centre, and gradually decreases as we move towards the circumference of the sphere, where it is absolute zero. The law of this temperature is as follows: If ${\displaystyle R}$ be the radius of the sphere, and ${\displaystyle r}$ the distance of the point considered from the centre, the absolute temperature will be proportional to ${\displaystyle R^{2}-r^{2}}$. Further, I shall suppose that in this world all bodies have the same co-efficient of dilatation, so that the linear dilatation of any body is proportional to its absolute temperature. Finally, I shall assume that a body transported from one point to another of different temperature is instantaneously in thermal equilibrium with its new environment. ... If they construct a geometry, it will not be like ours, which is the study of the movements of our invariable solids; it will be the study of the changes of position which they will have thus distinguished, and will be 'non-Euclidean displacements,' and this will be non-Euclidean geometry. So that beings like ourselves, educated in such a world, will not have the same geometry as ours." (pp.65-68)

Poincaré's disk was an important piece of evidence for the hypothesis that the choice of spatial geometry is conventional rather than factual, especially in the influential philosophical discussions of Rudolf Carnap and of Hans Reichenbach.

Lines and distance

Hyperbolic straight lines or geodesics consist of all arcs of Euclidean circles contained within the disk that are orthogonal to the boundary of the disk, plus all diameters of the disk.

Distances in this model are Cayley–Klein metrics. Given two distinct points p and q inside the disk, the unique hyperbolic line connecting them intersects the boundary at two ideal points, a and b. Label them so that the points are, in order, a, p, q, b, that is, so that |aq| > |ap| and |pb| > |qb|.

The hyperbolic distance between p and q is then

$${\displaystyle d(p,q)=\ln {\frac {\left|aq\right|\,\left|pb\right|}{\left|ap\right|\,\left|qb\right|}}.}$$

The vertical bars indicate Euclidean length of the line segment connecting the points between them in the model (not along the circle arc); ln is the natural logarithm.

Equivalently, if u and v are two vectors in real n-dimensional vector space R with the usual Euclidean norm, both of which have norm less than 1, then we may define an isometric invariant by

${\displaystyle \delta (u,v)=2{\frac {\lVert u-v\rVert ^{2}}{(1-\lVert u\rVert ^{2})(1-\lVert v\rVert ^{2})}}\,,}$

where ${\displaystyle \lVert \cdot \rVert }$ denotes the usual Euclidean norm. Then the distance function is

${\displaystyle {\begin{aligned}d(u,v)&=\operatorname {arcosh} (1+\delta (u,v))\\&=2\operatorname {arsinh} {\sqrt {\frac {\delta (u,v)}{2}}}\\\,&=2\ln {\frac {\lVert u-v\rVert +{\sqrt {\lVert u\rVert ^{2}\lVert v\rVert ^{2}-2u\cdot v+1}}}{\sqrt {(1-\lVert u\rVert ^{2})(1-\lVert v\rVert ^{2})}}}.\end{aligned}}}$

Such a distance function is defined for any two vectors of norm less than one, and makes the set of such vectors into a metric space which is a model of hyperbolic space of constant curvature −1. The model has the conformal property that the angle between two intersecting curves in hyperbolic space is the same as the angle in the model.

Specializing to the case where one of the points is the origin and the Euclidean distance between the points is r, the hyperbolic distance is: $${\displaystyle \ln \left({\frac {1+r}{1-r}}\right)=2\operatorname {artanh} r}$$ where ${\displaystyle \operatorname {artanh} }$ is the inverse hyperbolic function of the hyperbolic tangent. If the two points lie on the same radius and point ${\displaystyle x'=(r',\theta )}$ lies between the origin and point ${\displaystyle x=(r,\theta )}$ , their hyperbolic distance is $${\displaystyle \ln \left({\frac {1+r}{1-r}}\cdot {\frac {1-r'}{1+r'}}\right)=2(\operatorname {artanh} r-\operatorname {artanh} r').}$$ This reduces to the previous special case if ${\displaystyle r'=0}$.

Metric and curvature

The associated metric tensor of the Poincaré disk model is given by

${\displaystyle ds^{2}=4{\frac {\sum _{i}dx_{i}^{2}}{\left(1-\sum _{i}x_{i}^{2}\right)^{2}}}={\frac {4\,\lVert d\mathbf {x} \rVert {\vphantom {l}}^{2}}{{\bigl (}1-\lVert \mathbf {x} \rVert {\vphantom {l}}^{2}{\bigr )}^{2}}}}$

where the x_i are the Cartesian coordinates of the ambient Euclidean space.

An orthonormal frame with respect to this Riemannian metric is given by

${\displaystyle e_{i}={\frac {1}{2}}{\Bigl (}1-|\mathbf {x} |^{2}{\Bigr )}{\frac {\partial }{\partial x^{i}}},}$

with dual coframe of 1-forms

${\displaystyle \theta ^{i}={\frac {2}{1-|\mathbf {x} |{\vphantom {l}}^{2}}}\,dx^{i}.}$

In two dimensions

In two dimensions, with respect to these frames and the Levi-Civita connection, the connection forms are given by the unique skew-symmetric matrix of 1-forms ${\displaystyle \omega }$ that is torsion-free, i.e., that satisfies the matrix equation ${\displaystyle 0=d\theta +\omega \wedge \theta }$. Solving this equation for ${\displaystyle \omega }$ yields

${\displaystyle \omega ={\frac {2(y\,dx-x\,dy)}{1-|\mathbf {x} |{\vphantom {l}}^{2}}}{\begin{pmatrix}0&1\\-1&0\end{pmatrix}},}$

where the curvature matrix is

${\displaystyle \Omega =d\omega +\omega \wedge \omega =d\omega +0={\frac {-4\,dx\wedge dy}{{\bigl (}1-|\mathbf {x} |{\vphantom {l}}^{2}{\bigr )}^{2}}}{\begin{pmatrix}0&1\\-1&0\end{pmatrix}}.}$

Therefore, the curvature of the hyperbolic disk is

${\displaystyle K=\Omega _{2}^{1}(e_{1},e_{2})=-1.}$

Construction of lines

By compass and straightedge

The unique hyperbolic line through two points ${\displaystyle P}$ and ${\displaystyle Q}$ not on a diameter of the boundary circle can be constructed by:

• let ${\displaystyle P'}$ be the inversion in the boundary circle of point ${\displaystyle P}$
• let ${\displaystyle Q'}$ be the inversion in the boundary circle of point ${\displaystyle Q}$
• let ${\displaystyle M}$ be the midpoint of segment ${\displaystyle PP'}$
• let ${\displaystyle N}$ be the midpoint of segment ${\displaystyle QQ'}$
• Draw line ${\displaystyle m}$ through ${\displaystyle M}$ perpendicular to segment ${\displaystyle PP'}$
• Draw line ${\displaystyle n}$ through ${\displaystyle N}$ perpendicular to segment ${\displaystyle QQ'}$
• let ${\displaystyle C}$ be where line ${\displaystyle m}$ and line ${\displaystyle n}$ intersect.
• Draw circle ${\displaystyle c}$ with center ${\displaystyle C}$ and going through ${\displaystyle P}$ (and ${\displaystyle Q}$).
• The part of circle ${\displaystyle c}$ that is inside the disk is the hyperbolic line.

If P and Q are on a diameter of the boundary circle that diameter is the hyperbolic line.

Another way is:

• let ${\displaystyle M}$ be the midpoint of segment ${\displaystyle PQ}$
• Draw line m through ${\displaystyle M}$ perpendicular to segment ${\displaystyle PQ}$
• let ${\displaystyle P'}$ be the inversion in the boundary circle of point ${\displaystyle P}$
• let ${\displaystyle N}$ be the midpoint of segment ${\displaystyle PP'}$
• Draw line ${\displaystyle n}$ through ${\displaystyle N}$ perpendicular to segment ${\displaystyle PP'}$
• let ${\displaystyle C}$ be where line ${\displaystyle m}$ and line ${\displaystyle n}$ intersect.
• Draw circle ${\displaystyle c}$ with center ${\displaystyle C}$ and going through ${\displaystyle P}$ (and ${\displaystyle Q}$).
• The part of circle ${\displaystyle c}$ that is inside the disk is the hyperbolic line.

By analytic geometry

A basic construction of analytic geometry is to find a line through two given points. In the Poincaré disk model, lines in the plane are defined by portions of circles having equations of the form

${\displaystyle x^{2}+y^{2}+ax+by+1=0\,,}$

which is the general form of a circle orthogonal to the unit circle, or else by diameters. Given two points u = (u₁,u₂) and v = (v₁,v₂) in the disk which do not lie on a diameter, we can solve for the circle of this form passing through both points, and obtain

${\displaystyle {\begin{aligned}x^{2}+y^{2}&{}+{\frac {u_{2}(v_{1}^{2}+v_{2}^{2}+1)-v_{2}(u_{1}^{2}+u_{2}^{2}+1)}{u_{1}v_{2}-u_{2}v_{1}}}x\\&{}+{\frac {v_{1}(u_{1}^{2}+u_{2}^{2}+1)-u_{1}(v_{1}^{2}+v_{2}^{2}+1)}{u_{1}v_{2}-u_{2}v_{1}}}y+1=0\,.\end{aligned}}}$

If the points u and v are points on the boundary of the disk not lying at the endpoints of a diameter, the above simplifies to

${\displaystyle x^{2}+y^{2}+{\frac {2(u_{2}-v_{2})}{u_{1}v_{2}-u_{2}v_{1}}}x+{\frac {2(v_{1}-u_{1})}{u_{1}v_{2}-u_{2}v_{1}}}y+1=0\,.}$

Angles

We may compute the angle between the circular arc whose endpoints (ideal points) are given by unit vectors u and v, and the arc whose endpoints are s and t, by means of a formula. Since the ideal points are the same in the Klein model and the Poincaré disk model, the formulas are identical for each model.

If both models' lines are diameters, so that v = −u and t = −s, then we are merely finding the angle between two unit vectors, and the formula for the angle θ is

${\displaystyle \cos(\theta )=u\cdot s\,.}$

If v = −u but not t = −s, the formula becomes, in terms of the wedge product (${\displaystyle \wedge }$),

${\displaystyle \cos ^{2}(\theta )={\frac {P^{2}}{QR}},}$

where

${\displaystyle P=u\cdot (s-t)\,,}$

${\displaystyle Q=u\cdot u\,,}$

${\displaystyle R=(s-t)\cdot (s-t)-(s\wedge t)\cdot (s\wedge t)\,.}$

If both chords are not diameters, the general formula obtains

${\displaystyle \cos ^{2}(\theta )={\frac {P^{2}}{QR}}\,,}$

where

${\displaystyle P=(u-v)\cdot (s-t)-(u\wedge v)\cdot (s\wedge t)\,,}$

${\displaystyle Q=(u-v)\cdot (u-v)-(u\wedge v)\cdot (u\wedge v)\,,}$

${\displaystyle R=(s-t)\cdot (s-t)-(s\wedge t)\cdot (s\wedge t)\,.}$

Using the Binet–Cauchy identity and the fact that these are unit vectors we may rewrite the above expressions purely in terms of the dot product, as

${\displaystyle P=(u-v)\cdot (s-t)+(u\cdot t)(v\cdot s)-(u\cdot s)(v\cdot t)\,.}$

${\displaystyle Q=(1-u\cdot v)^{2}\,,}$

${\displaystyle R=(1-s\cdot t)^{2}\,.}$

Cycles

In the Euclidean plane the generalized circles (curves of constant curvature) are lines and circles. On the sphere, they are great and small circles. In the hyperbolic plane, there are 4 distinct types of generalized circles or cycles: circles, horocycles, hypercycles, and geodesics (or "hyperbolic lines"). In the Poincaré disk model, all of these are represented by straight lines or circles.

A Euclidean circle:

• that is completely inside the disk is a hyperbolic circle;
• that is inside the disk and tangent to the boundary is a horocycle;
• that intersects the boundary orthogonally is a hyperbolic line; and
• that intersects the boundary non-orthogonally is a hypercycle.

A Euclidean chord of the boundary circle:

• that goes through the center is a hyperbolic line; and
• that does not go through the center is a hypercycle.

Circles

A circle (the set of all points in a plane that are at a given distance from a given point, its center) is a circle completely inside the disk not touching or intersecting its boundary. The hyperbolic center of the circle in the model does not in general correspond to the Euclidean center of the circle, but they are on the same radius of the Poincare disk. (The Euclidean center is always closer to the center of the disk than the hyperbolic center.)

Hypercycles

A hypercycle (the set of all points in a plane that are on one side and at a given distance from a given line, its axis) is a Euclidean circle arc or chord of the boundary circle that intersects the boundary circle at a positive but non-right angle. Its axis is the hyperbolic line that shares the same two ideal points. This is also known as an equidistant curve.

Horocycles

A horocycle (a curve whose normal or perpendicular geodesics are limiting parallels, all converging asymptotically to the same ideal point), is a circle inside the disk that is tangent to the boundary circle of the disk. The point where it touches the boundary circle is not part of the horocycle. It is an ideal point and is the hyperbolic center of the horocycle. It is also the point to which all the perpendicular geodesics converge.

In the Poincaré disk model, the Euclidean points representing opposite "ends" of a horocycle converge to its center on the boundary circle, but in the hyperbolic plane every point of a horocycle is infinitely far from its center, and opposite ends of the horocycle are not connected. (Euclidean intuition can be misleading because the scale of the model increases to infinity at the boundary circle.)

Relation to other models of hyperbolic geometry

Relation to the Klein disk model

The Beltrami–Klein model (or Klein disk model) and the Poincaré disk are both models that project the whole hyperbolic plane in a disk. The two models are related through a projection on or from the hemisphere model. The Klein disk model is an orthographic projection to the hemisphere model while the Poincaré disk model is a stereographic projection.

An advantage of the Klein disk model is that lines in this model are Euclidean straight chords. A disadvantage is that the Klein disk model is not conformal (circles and angles are distorted).

When projecting the same lines in both models on one disk both lines go through the same two ideal points. (the ideal points remain on the same spot) also the pole of the chord in the Klein disk model is the center of the circle that contains the arc in the Poincaré disk model.

A point (x,y) in the Poincaré disk model maps to ${\textstyle \left({\frac {2x}{1+x^{2}+y^{2}}}\ ,\ {\frac {2y}{1+x^{2}+y^{2}}}\right)}$ in the Klein model.

A point (x,y) in the Klein model maps to ${\textstyle \left({\frac {x}{1+{\sqrt {1-x^{2}-y^{2}}}}}\ ,\ \ {\frac {y}{1+{\sqrt {1-x^{2}-y^{2}}}}}\right)}$ in the Poincaré disk model.

For ideal points ${\displaystyle x^{2}+y^{2}=1}$ and the formulas become ${\displaystyle x=x\ ,\ y=y}$ so the points are fixed.

If ${\displaystyle u}$ is a vector of norm less than one representing a point of the Poincaré disk model, then the corresponding point of the Klein disk model is given by: $${\displaystyle s={\frac {2u}{1+u\cdot u}}.}$$

Conversely, from a vector ${\displaystyle s}$ of norm less than one representing a point of the Beltrami–Klein model, the corresponding point of the Poincaré disk model is given by: $${\displaystyle u={\frac {s}{1+{\sqrt {1-s\cdot s}}}}={\frac {\left(1-{\sqrt {1-s\cdot s}}\right)s}{s\cdot s}}.}$$

Relation to the Poincaré half-plane model

The Poincare disk model and the Poincaré half-plane model are related by a Möbius transformation. If ${\displaystyle u\in \mathbb {D} }$ is a complex number of norm less than one representing a point of the Poincaré disk model, then the corresponding point ${\displaystyle z\in \mathbb {H} }$ of the upper half plane is given by the inverse of the Cayley transform ${\textstyle C:\mathbb {H} \to \mathbb {D} }$: $${\displaystyle C^{-1}(u)=z=i{\frac {1+u}{1-u}}.}$$Under ${\displaystyle C^{-1}}$, the points ${\displaystyle \{0,1,-i,i\}\in \mathbb {D} }$ are mapped to ${\displaystyle \{i,\infty ,1,-1\}\in \mathbb {H} }$.

In terms of real coordinates, a point (x,y) in the disk model maps to ${\textstyle \left({\frac {2x}{x^{2}+(1-y)^{2}}}\ ,\ {\frac {1-x^{2}-y^{2}}{x^{2}+(1-y)^{2}}}\right)\,}$ in the halfplane model.

A point (x,y) in the halfplane model maps to ${\textstyle \left({\frac {2x}{x^{2}+(1+y)^{2}}}\ ,\ {\frac {x^{2}+y^{2}-1}{x^{2}+(1+y)^{2}}}\right)\,}$ in the disk model.

Relation to the hyperboloid model

The Poincaré disk model, as well as the Klein model, are related to the hyperboloid model projectively. If we have a point on the upper sheet of the hyperboloid of the hyperboloid model, thereby defining a point in the hyperboloid model, we may project it onto the hyperplane t = 0 by intersecting it with a line drawn through . The result is the corresponding point of the Poincaré disk model.

For Cartesian coordinates (t, x_i) on the hyperboloid and (y_i) on the plane, the conversion formulas are: $${\displaystyle y_{i}={\frac {x_{i}}{1+t}}}$$ $${\displaystyle (t,x_{i})={\frac {\left(1+\sum {y_{i}^{2}},\,2y_{i}\right)}{1-\sum {y_{i}^{2}}}}\,.}$$

Compare the formulas for stereographic projection between a sphere and a plane.

• The hyperboloid model can be represented as the equation t = x₁ + x₂ + 1, t > 1. It can be used to construct a Poincaré disk model as a projection viewed from (t = −1, x₁ = 0, x₂ = 0), projecting the upper half hyperboloid onto the unit disk at t = 0. The red geodesic in the Poincaré disk model projects to the brown geodesic on the green hyperboloid.
• Animation of a partial {7,3} hyperbolic tiling of the hyperboloid rotated into the Poincare perspective.

Artistic realizations

M. C. Escher explored the concept of representing infinity on a two-dimensional plane. Discussions with Canadian mathematician H.S.M. Coxeter around 1956 inspired Escher's interest in hyperbolic tessellations, which are regular tilings of the hyperbolic plane. Escher's wood engravings Circle Limit I–IV demonstrate this concept between 1958 and 1960, the final one being Circle Limit IV: Heaven and Hell in 1960. According to Bruno Ernst, the best of them is Circle Limit III.

HyperRogue, a roguelike game, uses the hyperbolic plane for its world geometry, and also uses the Poincaré disk model.

See also

• Hyperbolic geometry
• Beltrami–Klein model
• Poincaré half-plane model
• Poincaré metric
• Pseudosphere
• Hyperboloid model
• Inversive geometry
• Uniform tilings in hyperbolic plane

References

1. Penrose, Roger (2004). The Road To Reality: A Complete Guide to the Laws of the Universe. Great Britain: Jonathan Cape. p. 45. ISBN 0-224-04447-8.
2. Milnor, John W. "Hyperbolic geometry: the first 150 years." Bulletin of the American Mathematical Society 6, no. 1 (1982): 9-24. B. Riemann, "Ueber die Hypothesen welche der Geometrie zu Grunde liegen", Abh. K. G. Wiss. Göttingen 13 (from his Inaugural Address of 1854).

   Eugenio Beltrami. "Teoria fondamentale degli spazii di curvatura costante", Annali di mat. ser. II 2, 232-255 (Op. Mat. 1, 406-429; Ann. École Norm. Sup. 6 (1869), 345-375).

3. Poincaré, H. (1882-12-01). "Théorie des groupes fuchsiens". Acta Mathematica (in French). 1 (1): 1–62. doi:10.1007/BF02592124. ISSN 1871-2509. S2CID 120406828.
4. ^ Poincaré, Henri (1905). Science and hypothesis. Robarts - University of Toronto. London W. Scott.
5. Carus, A. W.; Friedman, Michael; Kienzler, Wolfgang; Richardson, Alan; Schlotter, Sven (2019-06-25). Rudolf Carnap: Early Writings: The Collected Works of Rudolf Carnap, Volume 1. Oxford University Press. ISBN 978-0-19-106526-2.
6. Reichenbach, Hans (2012-03-13). The Philosophy of Space and Time. Courier Corporation. ISBN 978-0-486-13803-9.
7. Berger, Marcel (1987) . "9.6 The Poincaré Model". Geometry II. Translated by Cole, M.; Levy, S. Springer. p. 339.
8. "Comparing metric tensors of the Poincare and the Klein disk models of hyperbolic geometry". Stack Exchange. May 23, 2015.
9. Escher's Circle Limit Exploration

Further reading

• James W. Anderson, Hyperbolic Geometry, second edition, Springer, 2005.
• Eugenio Beltrami, Teoria fondamentale degli spazii di curvatura costante, Annali. di Mat., ser II 2 (1868), 232–255.
• Saul Stahl, The Poincaré Half-Plane, Jones and Bartlett, 1993.

External links

• Media related to Poincaré disk models at Wikimedia Commons

• Multi-dimensional geometry
• Hyperbolic geometry
• Henri Poincaré