Misplaced Pages

Selected point groups in three dimensions

Involutional symmetry Cs, (*) =	Cyclic symmetry Cnv, (*nn) =	Dihedral symmetry Dnh, (*n22) =
Polyhedral group, , (*n32)
Tetrahedral symmetry Td, (*332) =	Octahedral symmetry Oh, (*432) =	Icosahedral symmetry Ih, (*532) =

In geometry, the polyhedral group is any of the symmetry groups of the Platonic solids.

Groups

There are three polyhedral groups:

• The tetrahedral group of order 12, rotational symmetry group of the regular tetrahedron. It is isomorphic to A₄.
  • The conjugacy classes of T are:
    • identity
    • 4 × rotation by 120°, order 3, cw
    • 4 × rotation by 120°, order 3, ccw
    • 3 × rotation by 180°, order 2
• The octahedral group of order 24, rotational symmetry group of the cube and the regular octahedron. It is isomorphic to S₄.
  • The conjugacy classes of O are:
    • identity
    • 6 × rotation by ±90° around vertices, order 4
    • 8 × rotation by ±120° around triangle centers, order 3
    • 3 × rotation by 180° around vertices, order 2
    • 6 × rotation by 180° around midpoints of edges, order 2
• The icosahedral group of order 60, rotational symmetry group of the regular dodecahedron and the regular icosahedron. It is isomorphic to A₅.
  • The conjugacy classes of I are:
    • identity
    • 12 × rotation by ±72°, order 5
    • 12 × rotation by ±144°, order 5
    • 20 × rotation by ±120°, order 3
    • 15 × rotation by 180°, order 2

These symmetries double to 24, 48, 120 respectively for the full reflectional groups. The reflection symmetries have 6, 9, and 15 mirrors respectively. The octahedral symmetry, can be seen as the union of 6 tetrahedral symmetry mirrors, and 3 mirrors of dihedral symmetry Dih₂, . Pyritohedral symmetry is another doubling of tetrahedral symmetry.

The conjugacy classes of full tetrahedral symmetry, T_d ≅ S₄, are:

• identity
• 8 × rotation by 120°
• 3 × rotation by 180°
• 6 × reflection in a plane through two rotation axes
• 6 × rotoreflection by 90°

The conjugacy classes of pyritohedral symmetry, T_h, include those of T, with the two classes of 4 combined, and each with inversion:

• identity
• 8 × rotation by 120°
• 3 × rotation by 180°
• inversion
• 8 × rotoreflection by 60°
• 3 × reflection in a plane

The conjugacy classes of the full octahedral group, O_h ≅ S₄ × C₂, are:

• inversion
• 6 × rotoreflection by 90°
• 8 × rotoreflection by 60°
• 3 × reflection in a plane perpendicular to a 4-fold axis
• 6 × reflection in a plane perpendicular to a 2-fold axis

The conjugacy classes of full icosahedral symmetry, I_h ≅ A₅ × C₂, include also each with inversion:

• inversion
• 12 × rotoreflection by 108°, order 10
• 12 × rotoreflection by 36°, order 10
• 20 × rotoreflection by 60°, order 6
• 15 × reflection, order 2

Chiral polyhedral groups

Chiral polyhedral groups

Name (Orb.)	Coxeter notation	Order	Abstract structure	Rotation points #valence	Diagrams
					Orthogonal	Stereographic
T (332)		12	A4	43 32
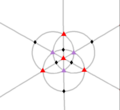
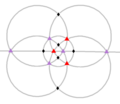
Th (3*2)		24	A4 × C2	43 3*2
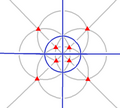
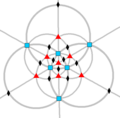
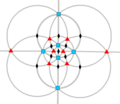
O (432)		24	S4	34 43 62
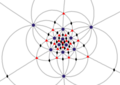
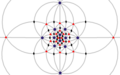
I (532)		60	A5	65 103 152

Full polyhedral groups

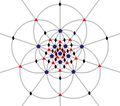
Full polyhedral groups

Weyl Schoe. (Orb.)	Coxeter notation	Order	Abstract structure	Coxeter number (h)	Mirrors (m)	Mirror diagrams
						Orthogonal	Stereographic
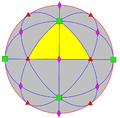
A3 Td (*332)		24	S4	4	6
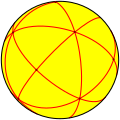B3 Oh (*432)		48	S4 × C2	8	3 >6
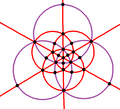H3 Ih (*532)		120	A5 × C2	10	15

See also

• Wythoff symbol
• List of spherical symmetry groups

References

• Coxeter, H. S. M. Regular Polytopes, 3rd ed. New York: Dover, 1973. (The Polyhedral Groups. §3.5, pp. 46–47)

External links

• Weisstein, Eric W. "PolyhedralGroup". MathWorld.

• Polyhedra