Triominoes is a variant of dominoes using triangular tiles published in 1965. A popular version of this game is marketed as Tri-Ominos by the Pressman Toy Corp.
Composition
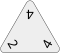
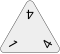
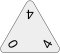
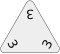
A triomino tile is in the shape of an equilateral triangle approximately 1 in (2.5 cm) on each side and approximately 1⁄4 in (6.4 mm) thick. Each point of the triangle has a number (most often from 0 to 5, as in the Pressman version), and each triomino has a unique combination of numbers, subject to the following restrictions:
- Any number is allowed to repeat in the combination. For example, 0-0-0 or 0-0-1 are possible combinations.
- When reading the numbers sequentially clockwise, starting with the lowest value, the numbers are not allowed to decrease. For example, 0-1-2 and 0-2-3 are possible, but 0-2-1 is not allowed.
Given these restrictions, with the six potential values (0–5) commonly seen, there are 56 unique combinations, and thus the standard triomino set has 56 tiles. Larger sets are possible; for example, including 6 as a possible end number would result in 84 tiles.
Tiles are most often made from plastic or resin that approximates the feel of stone or ivory, similar to most modern commercial domino sets. Numbers are recessed into the surface and painted black. Some "deluxe" sets include a raised, brass tack head in the center. This addition to the sets assists in mixing up or shuffling tiles, as the tack head reduces the surface area of the tile contacting the table, so tiles move more freely.
Playing the game
Setup and initial move
At the start of the game, all of the tiles are placed face down and shuffled. Players randomly draw their starting pieces. The specific number depends upon the number of players: a two-player game uses nine pieces per player to start, three or four players use seven pieces, and five or six players use six pieces. The tiles after the draw are kept face-down for later use.
One player keeps score for all, using columns for each player and cumulative scores.
- Starting examples
-
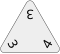
 Placing a triple-4 tile to start gives the player a score of 22 points (4×3 + 10 point bonus)
Placing a triple-4 tile to start gives the player a score of 22 points (4×3 + 10 point bonus)
-
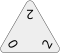
 Placing a triple-0 tile to start gives the player a score of 40 points (30 points for triple-0 + 10 point bonus)
Placing a triple-0 tile to start gives the player a score of 40 points (30 points for triple-0 + 10 point bonus)
-
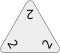
 Placing a 2-4-5 tile to start gives the player a score of 11 points (2+4+5, no bonus)
Placing a 2-4-5 tile to start gives the player a score of 11 points (2+4+5, no bonus)
The player who draws the largest "triple" (all three numbers the same on the tile), begins the game by placing that tile. That player scores 10 points plus the total value of the tile. The exception is that if the triple zero tile is used to start, that player earns 40 points. In this case, the only triple tile held is the triple zero, which would otherwise be trumped by any other triple tile.
If no triple is held by any player, the player with the highest single tile value plays it and scores its value without the 10 point bonus. Tile values are computed by summing the three numbers. For example, the 2-4-5 tile is worth 2+4+5=11 points. When two or more players hold tiles with the same summed value, the next highest counts and so on until there is the highest value tile.
Placement
- Legal placement examples
-
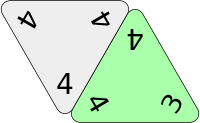 The legal placement of the 3-4-4 tile scores 3+4+4=11 points. Note how the corner values are matched to the adjacent 4-4-4 tile.
The legal placement of the 3-4-4 tile scores 3+4+4=11 points. Note how the corner values are matched to the adjacent 4-4-4 tile.
-
 The legal placement of the 2-5-5 tile scores 12 points.
The legal placement of the 2-5-5 tile scores 12 points.
Play proceeds clockwise; each player places a tile from their hand that lines up with the already placed tiles. A valid play of a triomino is similar to that of a domino in that the sides contacting each other must have matching numbers; this means the two numbers at the corners must match with the adjacent tile. A side with a 1 and a 2 will often not match the side the player is attempting to match. If a new tile is being placed such that it would touch two other tiles, then all of the adjacent numbers must match. Where the points of tiles meet the numbers must always be the same; if they are not, someone has been allowed to misplace a tile and the round must be restarted.
Points are scored based on the numbers on the tile played, with additional bonuses applied when special placements are made. After a tile has been placed legally, each number on the newly placed tile is summed and added to that player's score. (E.g. 5 + 3 + 1 = 9).
Drawing penalty
If a player cannot place a piece using the tiles in their hand, they must draw a new piece from the remaining pile. Each tile drawn penalizes the player 5 points. Players must continue to draw until a matching tile is found or until they have drawn three tiles. If one of the three can be placed the score is the value of the tile placed less the penalty, which may be positive or negative, depending on the placed tile value and number of tiles drawn. If none of these three tiles can be placed the penalty is 25 points.
If there are no remaining tiles left to be drawn and a player is unable to place a tile, they lose 10 points. For example, if there are two tiles left, a player without a tile to be placed may draw them (receiving a penalty -10 in total for the two tiles drawn), and if that player still has no tile that can be played, the additional end penalty is incurred (total penalty -10 + -10).
Bonus placement scores
- Bonus placement examples
-
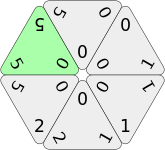 The completion of the hexagon with the 0-5-5 tile scores 0+5+5 + 50 (bonus) = 60 points in total. Note how all three values on the placed 0-5-5 tile must match the two adjacent tiles.
The completion of the hexagon with the 0-5-5 tile scores 0+5+5 + 50 (bonus) = 60 points in total. Note how all three values on the placed 0-5-5 tile must match the two adjacent tiles.
-
 The completion of the bridge with the 1-4-4 tile scores 1+4+4 + 40 (bonus) = 49 points in total. Note how the corner value 1 must match the adjacent corners.
The completion of the bridge with the 1-4-4 tile scores 1+4+4 + 40 (bonus) = 49 points in total. Note how the corner value 1 must match the adjacent corners.
-
 The completion of the bridge with the 1-2-5 tile scored 1+2+5+40 = 48 points. The bridge was then augmented with the 1-1-5 tile, which scored 1+1+5+40 = 47 points, as that player was required to match two adjacent sides.
The completion of the bridge with the 1-2-5 tile scored 1+2+5+40 = 48 points. The bridge was then augmented with the 1-1-5 tile, which scored 1+1+5+40 = 47 points, as that player was required to match two adjacent sides.
When a player can place a tile that completes a closed hexagonal shape (i.e. the 6th piece & all 3 numbers match), that player receives a bonus of 50 points plus the regular score for a legally placed tile, less any penalty if pieces have been drawn. If a player completes two hexagons in one move the player receives a 100 point bonus.
Bridges are made by matching one side of the tile and the point opposite. If a bridge is completed or a tile is added to a bridge, that player receives a 40-point bonus in addition to the tile's points, less any penalty if pieces have been drawn.
Round ending and objective
The round ends when no player can place a tile, whether or not all the face-down tiles have been drawn, or when one player runs out of tiles.
- When the round ends because no one can place a piece, then the player with the lowest total value hand gains the value in excess of their hand from each other player. For example, if the total value of the remaining tiles in Player B's hand is 15, while Player A's remaining hand sums to 23 and Player C's hand sums to 27, Player B will receive a total bonus of 20, which is the sum of the differences between B and A (23-15=8) and B and C (27-15=12).
- A player who is able to empty their hand and place their last tile receives 25 bonus points, plus the total of all of the remaining tiles in their opponent(s)' hands. This is consistent with the prior ending condition, as the player who emptied their hand has the lowest remaining total value (0).
Additional rounds are played until one player reaches a total of 400 points. They are not yet the winner, and may not be: this only signals that this is the last round, even if penalties later reduce their total below 400. The winner is the one who has the most points at the end of this last round.
Tile symmetry and strategy

- The red hexagon outline shows where a completed hexagon has been played.
- The green hexagon shows where the green 1-1-3 tile may be played to complete a hexagon.
- The blue hexagon shows where the blue 3-4-4 tile may be played to complete a different hexagon.
- The purple dashed hexagon shows where the hexagon cannot be completed because the tile required, illustrated in purple as 0-2-1, does not exist.
- The yellow line shows where a bridge could be formed with the yellow 0-2-3 tile, but this is no longer possible as the 0-2-3 tile has already been played. Also, the hexagon above the yellow tile cannot be completed, as it would require another tile (0-3-2) which does not exist.
The game includes only 56 out of 76 possible tiles, omitting those tiles in which the numbers appear in clockwise descending order; i.e., where 0-1-2 is a possible tile, the mirror-image reflection 0-2-1 is not. Consequently, there are many situations in which no tile completes a bridge or hexagon. This lack of symmetry means the game has only one of two tile patterns with Cis–trans isomerism, i.e., with three different numbers on the tile.
With only one of the two patterns, there are 21 tiles with one or more of a particular number e.g. there are 21 tiles with one or more "5". There are 6 tiles with any combination of two numbers e.g. there are 6 tiles with one or more 4 and one or more 5. The count to arrive at 56 possible tiles goes then as follows:
- 21 with at least one 5
- 15 with at least one 4 (and no 5)
- 10 with at least one 3 (and no 4 or 5)
- 6 with at least one 2 (and no 3, 4, or 5)
- 3 with at least one 1 (and no 2, 3, 4, or 5)
- 1 with at least one 0 (and no 1, 2, 3, 4, or 5)
The last one is the triple zero obviously.
Much depends on the luck of the draw, but skill plays a part, even if a small one. Players should be aware that they hold a matching tile or tiles and need to decide whether or not to play them or in which order to play them for their best advantage. They should be aware of potential hexagons or bridges, to avoid misplacing a tile that could be valuable. A player may consider it worthwhile to set up potential hexagons and bridges since this may or may not be to his own benefit; they may even hold the necessary tile to use in his next move. He may feel that placing a tile to which others can be matched is preferable to placing it to form an "impossible" hexagon or bridge.
Mobile application
In 2009, an app for the iPhone was launched which licensed the Tri-ominos brand from Pressman. A new app was launched in 2015, coinciding with Triominos' 50th anniversary.
Variants
Variants manufactured by Pressman have included "Quad-Ominos", with square-shaped tiles, and "Picture Tri-Ominos".
See also
- Triangular Dominoes, a similar game patented in 1885, with values marked on the sides rather than the corners.
- Trioker, a domino-like game invented by Marc Odier in 1969, also played with tiles shaped like equilateral triangles; the corner values range from zero to four.
References
- Filiatreau, John (1978-01-22). "it's only a game". The Courier-Journal. p. G6. Retrieved 2021-08-08 – via Newspapers.com.
- "Tenacious Tri-Ominos Inventor – Allan Cowan". Growing Up With Games. 2014-04-24. Retrieved 2021-08-07.
- ^ "Rules for Deluxe Tri-Ominos" (PDF). Pressman Toy Corporation. 2009. Archived from the original (PDF) on May 8, 2021.
- Verdon, Joan (2011-02-13). "Gaining app-titude". The Record. pp. B1, B5. Retrieved 2021-08-08.
- "Tri-Ominos app for iOS". Metacritic. Retrieved 2021-08-07.
- "Top 2015 Toys - Triominos Toy Reviews". The Toy Insider. 2015-07-08. Retrieved 2021-08-07.
- "Pressman". Sioux City Journal. 1982-10-18. p. 52. Retrieved 2021-08-08 – via Newspapers.com.
External links
| Domino games | ||||||
|---|---|---|---|---|---|---|
| Domino games |
|  | ||||
| Domino links | ||||||