
| Part of a series on |
| Power engineering |
|---|
| Electric power conversion |
| Electric power infrastructure |
| Electric power systems components |
A rectifier is an electrical device that converts alternating current (AC), which periodically reverses direction, to direct current (DC), which flows in only one direction.
The process is known as rectification, since it "straightens" the direction of current. Physically, rectifiers take a number of forms, including vacuum tube diodes, wet chemical cells, mercury-arc valves, stacks of copper and selenium oxide plates, semiconductor diodes, silicon-controlled rectifiers and other silicon-based semiconductor switches. Historically, even synchronous electromechanical switches and motor-generator sets have been used. Early radio receivers, called crystal radios, used a "cat's whisker" of fine wire pressing on a crystal of galena (lead sulfide) to serve as a point-contact rectifier or "crystal detector".
Rectifiers have many uses, but are often found serving as components of DC power supplies and high-voltage direct current power transmission systems. Rectification may serve in roles other than to generate direct current for use as a source of power. As noted, rectifiers can serve as detectors of radio signals. In gas heating systems flame rectification is used to detect the presence of a flame.
Depending on the type of alternating current supply and the arrangement of the rectifier circuit, the output voltage may require additional smoothing to produce a uniform steady voltage. Many applications of rectifiers, such as power supplies for radio, television and computer equipment, require a steady constant DC voltage (as would be produced by a battery). In these applications the output of the rectifier is smoothed by an electronic filter, which may be a capacitor, choke, or set of capacitors, chokes and resistors, possibly followed by a voltage regulator to produce a steady voltage.
A device that performs the opposite function, that is converting DC to AC, is called an inverter.
Rectifier devices
Before the development of silicon semiconductor rectifiers, vacuum tube thermionic diodes and copper oxide- or selenium-based metal rectifier stacks were used. The first vacuum tube diodes designed for rectifier application in power supply circuits were introduced in April 1915 by Saul Dushman of General Electric. With the introduction of semiconductor electronics, vacuum tube rectifiers became obsolete, except for some enthusiasts of vacuum tube audio equipment. For power rectification from very low to very high current, semiconductor diodes of various types (junction diodes, Schottky diodes, etc.) are widely used.
Other devices that have control electrodes as well as acting as unidirectional current valves are used where more than simple rectification is required—e.g., where variable output voltage is needed. High-power rectifiers, such as those used in high-voltage direct current power transmission, employ silicon semiconductor devices of various types. These are thyristors or other controlled switching solid-state switches, which effectively function as diodes to pass current in only one direction.
Rectifier circuits
Rectifier circuits may be single-phase or multi-phase. Most low power rectifiers for domestic equipment are single-phase, but three-phase rectification is very important for industrial applications and for the transmission of energy as DC (HVDC).
Single-phase rectifiers
Half-wave rectification
In half-wave rectification of a single-phase supply, either the positive or negative half of the AC wave is passed, while the other half is blocked. Because only one half of the input waveform reaches the output, mean voltage is lower. Half-wave rectification requires a single diode in a single-phase supply, or three in a three-phase supply. Rectifiers yield a unidirectional but pulsating direct current; half-wave rectifiers produce far more ripple than full-wave rectifiers, and much more filtering is needed to eliminate harmonics of the AC frequency from the output.

The no-load output DC voltage of an ideal half-wave rectifier for a sinusoidal input voltage is:
where:
- Vdc, Vav – the DC or average output voltage,
- Vpeak, the peak value of the phase input voltages,
- Vrms, the root mean square (RMS) value of output voltage.
Full-wave rectification

A full-wave rectifier converts the whole of the input waveform to one of constant polarity (positive or negative) at its output. Mathematically, this corresponds to the absolute value function. Full-wave rectification converts both polarities of the input waveform to pulsating DC (direct current), and yields a higher average output voltage. Two diodes and a center-tapped transformer, or four diodes in a bridge configuration and any AC source (including a transformer without center tap), are needed. Single semiconductor diodes, double diodes with a common cathode or common anode, and four- or six-diode bridges are manufactured as single components.

For single-phase AC, if the transformer is center-tapped, then two diodes back-to-back (cathode-to-cathode or anode-to-anode, depending on output polarity required) can form a full-wave rectifier. Twice as many turns are required on the transformer secondary to obtain the same output voltage than for a bridge rectifier, but the power rating is unchanged.
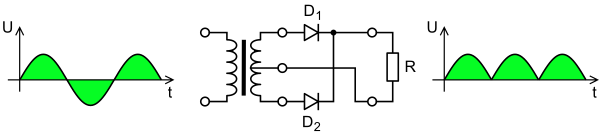
The average and RMS no-load output voltages of an ideal single-phase full-wave rectifier are:
Very common double-diode rectifier vacuum tubes contained a single common cathode and two anodes inside a single envelope, achieving full-wave rectification with positive output. The 5U4 and the 80/5Y3 (4 pin)/(octal) were popular examples of this configuration.
Three-phase rectifiers
Single-phase rectifiers are commonly used for power supplies for domestic equipment. However, for most industrial and high-power applications, three-phase rectifier circuits are the norm. As with single-phase rectifiers, three-phase rectifiers can take the form of a half-wave circuit, a full-wave circuit using a center-tapped transformer, or a full-wave bridge circuit.
Thyristors are commonly used in place of diodes to create a circuit that can regulate the output voltage. Many devices that provide direct current actually 'generate' three-phase AC. For example, an automobile alternator contains nine diodes, six of which function as a full-wave rectifier for battery charging.
Three-phase, half-wave circuit

An uncontrolled three-phase, half-wave midpoint circuit requires three diodes, one connected to each phase. This is the simplest type of three-phase rectifier but suffers from relatively high harmonic distortion on both the AC and DC connections. This type of rectifier is said to have a pulse-number of three, since the output voltage on the DC side contains three distinct pulses per cycle of the grid frequency:
The peak values of this three-pulse DC voltage are calculated from the RMS value of the input phase voltage (line to neutral voltage, 120 V in North America, 230 V within Europe at mains operation): . The average no-load output voltage results from the integral under the graph of a positive half-wave with the period duration of (from 30° to 150°):
Three-phase, full-wave circuit using center-tapped transformer
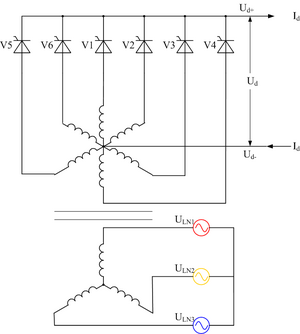
If the AC supply is fed via a transformer with a center tap, a rectifier circuit with improved harmonic performance can be obtained. This rectifier now requires six diodes, one connected to each end of each transformer secondary winding. This circuit has a pulse-number of six, and in effect, can be thought of as a six-phase, half-wave circuit.
Before solid state devices became available, the half-wave circuit, and the full-wave circuit using a center-tapped transformer, were very commonly used in industrial rectifiers using mercury-arc valves. This was because the three or six AC supply inputs could be fed to a corresponding number of anode electrodes on a single tank, sharing a common cathode.
With the advent of diodes and thyristors, these circuits have become less popular and the three-phase bridge circuit has become the most common circuit.
Three-phase bridge rectifier uncontrolled

For an uncontrolled three-phase bridge rectifier, six diodes are used, and the circuit again has a pulse number of six. For this reason, it is also commonly referred to as a six-pulse bridge. The B6 circuit can be seen simplified as a series connection of two three-pulse center circuits.
For low-power applications, double diodes in series, with the anode of the first diode connected to the cathode of the second, are manufactured as a single component for this purpose. Some commercially available double diodes have all four terminals available so the user can configure them for single-phase split supply use, half a bridge, or three-phase rectifier.
For higher-power applications, a single discrete device is usually used for each of the six arms of the bridge. For the very highest powers, each arm of the bridge may consist of tens or hundreds of separate devices in parallel (where very high current is needed, for example in aluminium smelting) or in series (where very high voltages are needed, for example in high-voltage direct current power transmission).

The pulsating DC voltage results from the differences of the instantaneous positive and negative phase voltages , phase-shifted by 30°:
The ideal, no-load average output voltage of the B6 circuit results from the integral under the graph of a DC voltage pulse with the period duration of (from 60° to 120°) with the peak value :

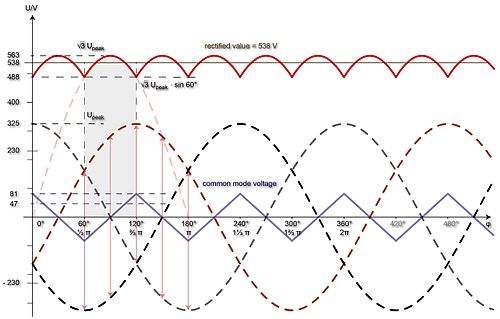
If the three-phase bridge rectifier is operated symmetrically (as positive and negative supply voltage), the center point of the rectifier on the output side (or the so-called isolated reference potential) opposite the center point of the transformer (or the neutral conductor) has a potential difference in the form of a triangular common-mode voltage. For this reason, these two centers must never be connected to each other, otherwise short-circuit currents would flow. The ground of the three-phase bridge rectifier in symmetrical operation is thus decoupled from the neutral conductor or the earth of the mains voltage. Powered by a transformer, earthing of the center point of the bridge is possible, provided that the secondary winding of the transformer is electrically isolated from the mains voltage and the star point of the secondary winding is not on earth. In this case, however, (negligible) leakage currents are flowing over the transformer windings.
The common-mode voltage is formed out of the respective average values of the differences between the positive and negative phase voltages, which form the pulsating DC voltage. The peak value of the delta voltage amounts 1/4 of the peak value of the phase input voltage and is calculated with minus half of the DC voltage at 60° of the period:
The RMS value of the common-mode voltage is calculated from the form factor for triangular oscillations:
If the circuit is operated asymmetrically (as a simple supply voltage with just one positive pole), both the positive and negative poles (or the isolated reference potential) are pulsating opposite the center (or the ground) of the input voltage analogously to the positive and negative waveforms of the phase voltages. However, the differences in the phase voltages result in the six-pulse DC voltage (over the duration of a period). The strict separation of the transformer center from the negative pole (otherwise short-circuit currents will flow) or a possible grounding of the negative pole when powered by an isolating transformer apply correspondingly to the symmetrical operation.
Three-phase bridge rectifier controlled
The controlled three-phase bridge rectifier uses thyristors in place of diodes. The output voltage is reduced by the factor cos(α):
Or, expressed in terms of the line to line input voltage:
where:
- VLLpeak is the peak value of the line to line input voltages,
- Vpeak is the peak value of the phase (line to neutral) input voltages, and
- α is the firing angle of the thyristor (0 if diodes are used to perform rectification)
The above equations are only valid when no current is drawn from the AC supply or in the theoretical case when the AC supply connections have no inductance. In practice, the supply inductance causes a reduction of DC output voltage with increasing load, typically in the range 10–20% at full load.
The effect of supply inductance is to slow down the transfer process (called commutation) from one phase to the next. As result of this is that at each transition between a pair of devices, there is a period of overlap during which three (rather than two) devices in the bridge are conducting simultaneously. The overlap angle is usually referred to by the symbol μ (or u), and may be 20 30° at full load.
With supply inductance taken into account, the output voltage of the rectifier is reduced to
The overlap angle μ is directly related to the DC current, and the above equation may be re-expressed as
where:
- Lc is the commutating inductance per phase, and
- Id is the direct current.
 |
 |
 |
 |
Twelve-pulse bridge

Although better than single-phase rectifiers or three-phase half-wave rectifiers, six-pulse rectifier circuits still produce considerable harmonic distortion on both the AC and DC connections. For very high-power rectifiers the twelve-pulse bridge connection is usually used. A twelve-pulse bridge consists of two six-pulse bridge circuits connected in series, with their AC connections fed from a supply transformer that produces a 30° phase shift between the two bridges. This cancels many of the characteristic harmonics the six-pulse bridges produce.
The 30-degree phase shift is usually achieved by using a transformer with two sets of secondary windings, one in star (wye) connection and one in delta connection.
Voltage-multiplying rectifiers
Main article: Voltage multiplier See also: Voltage doubler
The simple half-wave rectifier can be built in two electrical configurations with the diodes pointing in opposite directions, one version connects the negative terminal of the output direct to the AC supply and the other connects the positive terminal of the output direct to the AC supply. By combining both of these with separate output smoothing it is possible to get an output voltage of nearly double the peak AC input voltage. This also provides a tap in the middle, which allows use of such a circuit as a split rail power supply.
A variant of this is to use two capacitors in series for the output smoothing on a bridge rectifier then place a switch between the midpoint of those capacitors and one of the AC input terminals. With the switch open, this circuit acts like a normal bridge rectifier. With the switch closed, it acts like a voltage doubling rectifier. In other words, this makes it easy to derive a voltage of roughly 320 V (±15%, approx.) DC from any 120 V or 230 V mains supply in the world, this can then be fed into a relatively simple switched-mode power supply. However, for a given desired ripple, the value of both capacitors must be twice the value of the single one required for a normal bridge rectifier; when the switch is closed each one must filter the output of a half-wave rectifier, and when the switch is open the two capacitors are connected in series with an equivalent value of half one of them.
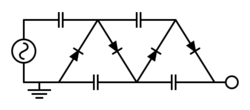
In a Cockcroft-Walton voltage multiplier, stages of capacitors and diodes are cascaded to amplify a low AC voltage to a high DC voltage. These circuits are capable of producing a DC output voltage potential up to about ten times the peak AC input voltage, in practice limited by current capacity and voltage regulation issues. Diode voltage multipliers, frequently used as a trailing boost stage or primary high voltage (HV) source, are used in HV laser power supplies, powering devices such as cathode-ray tubes (CRT) (like those used in CRT based television, radar and sonar displays), photon amplifying devices found in image intensifying and photo multiplier tubes (PMT), and magnetron based radio frequency (RF) devices used in radar transmitters and microwave ovens. Before the introduction of semiconductor electronics, transformerless vacuum tube receivers powered directly from AC power sometimes used voltage doublers to generate roughly 300 VDC from a 100–120 V power line.
Quantification of rectifiers
| This section is missing information about conversion ratios for at least three-phase half-wave and full-wave rectification, since these rectifiers have their own sections in this article.. Please expand the section to include this information. Further details may exist on the talk page. (October 2017) |
Several ratios are used to quantify the function and performance of rectifiers or their output, including transformer utilization factor (TUF), conversion ratio (η), ripple factor, form factor, and peak factor. The two primary measures are DC voltage (or offset) and peak-peak ripple voltage, which are constituent components of the output voltage.
Conversion ratio
Conversion ratio (also called "rectification ratio", and confusingly, "efficiency") η is defined as the ratio of DC output power to the input power from the AC supply. Even with ideal rectifiers, the ratio is less than 100% because some of the output power is AC power rather than DC which manifests as ripple superimposed on the DC waveform. The ratio can be improved with the use of smoothing circuits which reduce the ripple and hence reduce the AC content of the output. Conversion ratio is reduced by losses in transformer windings and power dissipation in the rectifier element itself. This ratio is of little practical significance because a rectifier is almost always followed by a filter to increase DC voltage and reduce ripple. In some three-phase and multi-phase applications the conversion ratio is high enough that smoothing circuitry is unnecessary. In other circuits, like filament heater circuits in vacuum tube electronics where the load is almost entirely resistive, smoothing circuitry may be omitted because resistors dissipate both AC and DC power, so no power is lost.
For a half-wave rectifier the ratio is very modest.
- (the divisors are 2 rather than √2 because no power is delivered on the negative half-cycle)
Thus maximum conversion ratio for a half-wave rectifier is,
Similarly, for a full-wave rectifier,
Three-phase rectifiers, especially three-phase full-wave rectifiers, have much greater conversion ratios because the ripple is intrinsically smaller.
For a three-phase half-wave rectifier,
For a three-phase full-wave rectifier,
Transformer utilization ratio
The transformer utilization factor (TUF) of a rectifier circuit is defined as the ratio of the DC power available at the input resistor to the AC rating of the output coil of a transformer.
The rating of the transformer can be defined as:
Rectifier voltage drop
See also: Diode § Forward threshold voltage for various semiconductors
A real rectifier characteristically drops part of the input voltage (a voltage drop, for silicon devices, of typically 0.7 volts plus an equivalent resistance, in general non-linear)—and at high frequencies, distorts waveforms in other ways. Unlike an ideal rectifier, it dissipates some power.
An aspect of most rectification is a loss from the peak input voltage to the peak output voltage, caused by the built-in voltage drop across the diodes (around 0.7 V for ordinary silicon p–n junction diodes and 0.3 V for Schottky diodes). Half-wave rectification and full-wave rectification using a center-tapped secondary produces a peak voltage loss of one diode drop. Bridge rectification has a loss of two diode drops. This reduces output voltage, and limits the available output voltage if a very low alternating voltage must be rectified. As the diodes do not conduct below this voltage, the circuit only passes current through for a portion of each half-cycle, causing short segments of zero voltage (where instantaneous input voltage is below one or two diode drops) to appear between each "hump".
Peak loss is very important for low voltage rectifiers (for example, 12 V or less) but is insignificant in high-voltage applications such as HVDC power transmission systems.
Harmonic distortion
Non-linear loads like rectifiers produce current harmonics of the source frequency on the AC side and voltage harmonics of the source frequency on the DC side, due to switching behavior.
Rectifier output smoothing
See also: Ripple (electrical) § Ripple voltage| This section does not cite any sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (October 2017) (Learn how and when to remove this message) |

While half-wave and full-wave rectification deliver unidirectional current, neither produces a constant voltage. There is a large AC ripple voltage component at the source frequency for a half-wave rectifier, and twice the source frequency for a full-wave rectifier. Ripple voltage is usually specified peak-to-peak. Producing steady DC from a rectified AC supply requires a smoothing circuit or filter. In its simplest form this can be just a capacitor (functioning as both a smoothing capacitor as well as a reservoir, buffer or bulk capacitor), choke, resistor, Zener diode and resistor, or voltage regulator placed at the output of the rectifier. In practice, most smoothing filters utilize multiple components to efficiently reduce ripple voltage to a level tolerable by the circuit.

The filter capacitor releases its stored energy during the part of the AC cycle when the AC source does not supply any power, that is, when the AC source changes its direction of flow of current.
Performance with low impedance source
The above diagram shows the voltage waveforms of the reservoir performance when supplied from a voltage source with near zero impedance, such as a mains supply. Both voltages start from zero at time t=0 at the far left of the image, then the capacitor voltage follows the rectified AC voltage as it increases, the capacitor is charged and current is supplied to the load. At the end of the mains quarter cycle, the capacitor is charged to the peak value Vp of the rectifier voltage. Following this, the rectifier input voltage starts to decrease to its minimum value Vmin as it enters the next quarter cycle. This initiates the discharge of the capacitor through the load while the capacitor holds up the output voltage to the load.
The size of the capacitor C is determined by the amount of ripple r that can be tolerated, where r=(Vp-Vmin)/Vp.
These circuits are very frequently fed from transformers, which may have significant internal impedance in the form of resistance and/or reactance. Transformer internal impedance modifies the reservoir capacitor waveform, changes the peak voltage, and introduces regulation issues.
Capacitor input filter
Main article: Capacitor-input filterFor a given load, sizing of a smoothing capacitor is a tradeoff between reducing ripple voltage and increasing ripple current. The peak current is set by the rate of rise of the supply voltage on the rising edge of the incoming sine-wave, reduced by the resistance of the transformer windings. High ripple currents increase IR losses (in the form of heat) in the capacitor, rectifier and transformer windings, and may exceed the ampacity of the components or VA rating of the transformer. Vacuum tube rectifiers specify the maximum capacitance of the input capacitor, and SS diode rectifiers also have current limitations. Capacitors for this application need low ESR, or ripple current may overheat them. To limit ripple voltage to a specified value the required capacitor size is proportional to the load current and inversely proportional to the supply frequency and the number of output peaks of the rectifier per input cycle. Full-wave rectified output requires a smaller capacitor because it is double the frequency of half-wave rectified output. To reduce ripple to a satisfactory limit with just a single capacitor would often require a capacitor of impractical size. This is because the ripple current rating of a capacitor does not increase linearly with size and there may also be height limitations. For high current applications banks of capacitors are used instead.
Choke input filter
It is also possible to put the rectified waveform into a choke-input filter. The advantage of this circuit is that the current waveform is smoother: current is drawn over the entire cycle, instead of being drawn in pulses at the peaks of AC voltage each half-cycle as in a capacitor input filter. The disadvantage is that the voltage output is much lower – the average of an AC half-cycle rather than the peak; this is about 90% of the RMS voltage versus times the RMS voltage (unloaded) for a capacitor input filter. Offsetting this is superior voltage regulation and higher available current, which reduce peak voltage and ripple current demands on power supply components. Inductors require cores of iron or other magnetic materials, and add weight and size. Their use in power supplies for electronic equipment has therefore dwindled in favour of semiconductor circuits such as voltage regulators.
Resistor as input filter
In cases where ripple voltage is insignificant, like battery chargers, the input filter may be a single series resistor to adjust the output voltage to that required by the circuit. A resistor reduces both output voltage and ripple voltage proportionately. A disadvantage of a resistor input filter is that it consumes power in the form of waste heat that is not available to the load, so it is employed only in low current circuits.
Higher order and cascade filters
To further reduce ripple, the initial filter element may be followed by additional alternating series and shunt filter components, or by a voltage regulator. Series filter components may be resistors or chokes; shunt elements may be resistors or capacitors. The filter may raise DC voltage as well as reduce ripple. Filters are often constructed from pairs of series/shunt components called RC (series resistor, shunt capacitor) or LC (series choke, shunt capacitor) sections. Two common filter geometries are known as Pi (capacitor, choke, capacitor) and T (choke, capacitor, choke) filters. Sometimes the series elements are resistors - because resistors are smaller and cheaper - when a lower DC output is desirable or permissible. Another kind of special filter geometry is a series resonant choke or tuned choke filter. Unlike the other filter geometries which are low-pass filters, a resonant choke filter is a band-stop filter: it is a parallel combination of choke and capacitor which resonates at the frequency of the ripple voltage, presenting a very high impedance to the ripple. It may be followed by a shunt capacitor to complete the filter.
Voltage regulators
A more usual alternative to additional filter components, if the DC load requires very low ripple voltage, is to follow the input filter with a voltage regulator. A voltage regulator operates on a different principle than a filter, which is essentially a voltage divider that shunts voltage at the ripple frequency away from the load. Rather, a regulator increases or decreases current supplied to the load in order to maintain a constant output voltage.
A simple passive shunt voltage regulator may consist of a series resistor to drop source voltage to the required level and a Zener diode shunt with reverse voltage equal to the set voltage. When input voltage rises, the diode dumps current to maintain the set output voltage. This kind of regulator is usually employed only in low voltage, low current circuits because Zener diodes have both voltage and current limitations. It is also very inefficient, because it dumps excess current, which is not available to the load.
A more efficient alternative to a shunt voltage regulator is an active voltage regulator circuit. An active regulator employs reactive components to store and discharge energy, so that most or all current supplied by the rectifier is passed to the load. It may also use negative and positive feedback in conjunction with at least one voltage amplifying component like a transistor to maintain output voltage when source voltage drops. The input filter must prevent the troughs of the ripple dropping below the minimum voltage required by the regulator to produce the required output voltage. The regulator serves both to significantly reduce the ripple and to deal with variations in supply and load characteristics.
Applications
See also: Capacitive power supplyThe primary application of rectifiers is to derive DC power from an AC supply (AC to DC converter). Rectifiers are used inside the power supplies of virtually all electronic equipment. AC/DC power supplies may be broadly divided into linear power supplies and switched-mode power supplies. In such power supplies, the rectifier will be in series following the transformer and be followed by a smoothing filter and possibly a voltage regulator.
Converting DC power from one voltage to another is much more complicated. One method of DC-to-DC conversion first converts power to AC (using a device called an inverter), then uses a transformer to change the voltage, and finally rectifies power back to DC. A frequency of typically several tens of kilohertz is used, as this requires much smaller inductance than at lower frequencies and obviates the use of heavy, bulky, and expensive iron-cored transformers. Another method of converting DC voltages uses a charge pump, using rapid switching to change the connections of capacitors; this technique is generally limited to supplies up to a couple of watts, owing to the size of capacitors required.
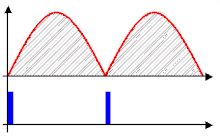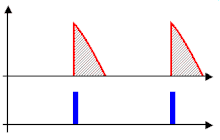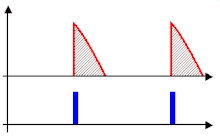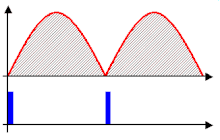
Rectifiers are also used for detection of amplitude modulated radio signals. The signal may be amplified before detection. If not, a very low voltage drop diode or a diode biased with a fixed voltage must be used. When using a rectifier for demodulation the capacitor and load resistance must be carefully matched: too low a capacitance makes the high frequency carrier pass to the output, and too high makes the capacitor just charge and stay charged.
Rectifiers supply polarized voltage for welding. In such circuits control of the output current is required; this is sometimes achieved by replacing some of the diodes in a bridge rectifier with thyristors, effectively diodes whose voltage output can be regulated by switching on and off with phase-fired controllers.
Thyristors are used in various classes of railway rolling stock systems so that fine control of the traction motors can be achieved. Gate turn-off thyristors are used to produce alternating current from a DC supply, for example on the Eurostar Trains to power the three-phase traction motors.
Rectification technologies
Electromechanical
Before about 1905 when tube-type rectifiers were developed, power conversion devices were purely electro-mechanical in design. Mechanical rectifiers used some form of rotation or resonant vibration driven by electromagnets, which operated a switch or commutator to reverse the current.
These mechanical rectifiers were noisy and had high maintenance requirements, including lubrication and replacement of moving parts due to wear. Opening mechanical contacts under load resulted in electrical arcs and sparks that heated and eroded the contacts. They also were not able to handle AC frequencies above several thousand cycles per second.
Synchronous rectifier
Main article: Synchronous rectificationTo convert alternating into direct current in electric locomotives, a synchronous rectifier may be used. It consists of a synchronous motor driving a set of heavy-duty electrical contacts. The motor spins in time with the AC frequency and periodically reverses the connections to the load at an instant when the sinusoidal current goes through a zero-crossing. The contacts do not have to switch a large current, but they must be able to carry a large current to supply the locomotive's DC traction motors.
Vibrating rectifier
Main article: Mechanical rectifier
These consisted of a resonant reed, vibrated by an alternating magnetic field created by an AC electromagnet, with contacts that reversed the direction of the current on the negative half cycles. They were used in low power devices, such as battery chargers, to rectify the low voltage produced by a step-down transformer. Another use was in battery power supplies for portable vacuum tube radios, to provide the high DC voltage for the tubes. These operated as a mechanical version of modern solid state switching inverters, with a transformer to step the battery voltage up, and a set of vibrator contacts on the transformer core, operated by its magnetic field, to repeatedly break the DC battery current to create a pulsing AC to power the transformer. Then a second set of rectifier contacts on the vibrator rectified the high AC voltage from the transformer secondary to DC.
Motor-generator set
Main articles: Motor-generator and Rotary converter
A motor-generator set, or the similar rotary converter, is not strictly a rectifier as it does not actually rectify current, but rather generates DC from an AC source. In an "M-G set", the shaft of an AC motor is mechanically coupled to that of a DC generator. The DC generator produces multiphase alternating currents in its armature windings, which a commutator on the armature shaft converts into a direct current output; or a homopolar generator produces a direct current without the need for a commutator. M-G sets are useful for producing DC for railway traction motors, industrial motors and other high-current applications, and were common in many high-power DC uses (for example, carbon-arc lamp projectors for outdoor theaters) before high-power semiconductors became widely available.
Electrolytic
The electrolytic rectifier was a device from the early twentieth century that is no longer used. A home-made version is illustrated in the 1913 book The Boy Mechanic but it would be suitable for use only at very low voltages because of the low breakdown voltage and the risk of electric shock. A more complex device of this kind was patented by G. W. Carpenter in 1928 (US Patent 1671970).
When two different metals are suspended in an electrolyte solution, direct current flowing one way through the solution sees less resistance than in the other direction. Electrolytic rectifiers most commonly used an aluminum anode and a lead or steel cathode, suspended in a solution of triammonium orthophosphate.
The rectification action is due to a thin coating of aluminium hydroxide on the aluminum electrode, formed by first applying a strong current to the cell to build up the coating. The rectification process is temperature-sensitive, and for best efficiency should not operate above 86 °F (30 °C). There is also a breakdown voltage where the coating is penetrated and the cell is short-circuited. Electrochemical methods are often more fragile than mechanical methods, and can be sensitive to usage variations, which can drastically change or completely disrupt the rectification processes.
Similar electrolytic devices were used as lightning arresters around the same era by suspending many aluminium cones in a tank of triammonium orthophosphate solution. Unlike the rectifier above, only aluminium electrodes were used, and used on A.C., there was no polarization and thus no rectifier action, but the chemistry was similar.
The modern electrolytic capacitor, an essential component of most rectifier circuit configurations was also developed from the electrolytic rectifier.
Plasma type
The development of vacuum tube technology in the early 20th century resulted in the invention of various tube-type rectifiers, which largely replaced the noisy, inefficient mechanical rectifiers.
Mercury-arc
Main article: Mercury-arc valve Early 3-phase industrial mercury vapor rectifier tube
Early 3-phase industrial mercury vapor rectifier tube 150 kV mercury-arc valve at Manitoba Hydro power station, Radisson, Canada converted AC hydropower to DC for transmission to distant cities.
150 kV mercury-arc valve at Manitoba Hydro power station, Radisson, Canada converted AC hydropower to DC for transmission to distant cities.
A rectifier used in high-voltage direct current (HVDC) power transmission systems and industrial processing between about 1909 to 1975 is a mercury-arc rectifier or mercury-arc valve. The device is enclosed in a bulbous glass vessel or large metal tub. One electrode, the cathode, is submerged in a pool of liquid mercury at the bottom of the vessel and one or more high purity graphite electrodes, called anodes, are suspended above the pool. There may be several auxiliary electrodes to aid in starting and maintaining the arc. When an electric arc is established between the cathode pool and suspended anodes, a stream of electrons flows from the cathode to the anodes through the ionized mercury, but not the other way (in principle, this is a higher-power counterpart to flame rectification, which uses the same one-way current transmission properties of the plasma naturally present in a flame).
These devices can be used at power levels of hundreds of kilowatts, and may be built to handle one to six phases of AC current. Mercury-arc rectifiers have been replaced by silicon semiconductor rectifiers and high-power thyristor circuits in the mid-1970s. The most powerful mercury-arc rectifiers ever built were installed in the Manitoba Hydro Nelson River Bipole HVDC project, with a combined rating of more than 1 GW and 450 kV.
Argon gas electron tube

The General Electric Tungar rectifier was a mercury vapor (ex.:5B24) or argon (ex.:328) gas-filled electron tube device with a tungsten filament cathode and a carbon button anode. It operated similarly to the thermionic vacuum tube diode, but the gas in the tube ionized during forward conduction, giving it a much lower forward voltage drop so it could rectify lower voltages. It was used for battery chargers and similar applications from the 1920s until lower-cost metal rectifiers, and later semiconductor diodes, supplanted it. These were made up to a few hundred volts and a few amperes rating, and in some sizes strongly resembled an incandescent lamp with an additional electrode.
The 0Z4 was a gas-filled rectifier tube commonly used in vacuum tube car radios in the 1940s and 1950s. It was a conventional full-wave rectifier tube with two anodes and one cathode, but was unique in that it had no filament (thus the "0" in its type number). The electrodes were shaped such that the reverse breakdown voltage was much higher than the forward breakdown voltage. Once the breakdown voltage was exceeded, the 0Z4 switched to a low-resistance state with a forward voltage drop of about 24 V.
Diode vacuum tube (valve)
See also: List of vacuum tubes
The thermionic vacuum tube diode, originally called the Fleming valve, was invented by John Ambrose Fleming in 1904 as a detector for radio waves in radio receivers, and evolved into a general rectifier. It consisted of an evacuated glass bulb with a filament heated by a separate current, and a metal plate anode. The filament emitted electrons by thermionic emission (the Edison effect), discovered by Thomas Edison in 1884, and a positive voltage on the plate caused a current of electrons through the tube from filament to plate. Since only the filament produced electrons, the tube would only conduct current in one direction, allowing the tube to rectify an alternating current.
Thermionic diode rectifiers were widely used in power supplies in vacuum tube consumer electronic products, such as phonographs, radios, and televisions, for example the All American Five radio receiver, to provide the high DC plate voltage needed by other vacuum tubes. "Full-wave" versions with two separate plates were popular because they could be used with a center-tapped transformer to make a full-wave rectifier. Vacuum tube rectifiers were made for very high voltages, such as the high voltage power supply for the CRT of television receivers, and the kenotron used for power supply in X-ray equipment. However, compared to modern semiconductor diodes, vacuum tube rectifiers have high internal resistance due to space charge and therefore high voltage drops, causing high power dissipation and low efficiency. They are rarely able to handle currents exceeding 250 mA owing to the limits of plate power dissipation, and cannot be used for low voltage applications, such as battery chargers. Another limitation of the vacuum tube rectifier is that the heater power supply often requires special arrangements to insulate it from the high voltages of the rectifier circuit.
Solid state
Crystal detector
Main article: Crystal detector
The crystal detector, the earliest type of semiconductor diode, was used as a detector in some of the earliest radio receivers, called crystal radios, to rectify the radio carrier wave and extract the modulation which produced the sound in the earphones. Invented by Jagadish Chandra Bose and G. W. Pickard around 1902, it was a significant improvement over earlier detectors such as the coherer. One popular type of crystal detector, often called a cat's whisker detector, consists of a crystal of some semiconducting mineral, usually galena (lead sulfide), with a light springy wire touching its surface. Its fragility and limited current capability made it unsuitable for power supply applications. It was used widely in radios until the 1920s when vacuum tubes replaced it. In the 1930s, researchers miniaturized and improved the crystal detector for use at microwave frequencies, developing the first semiconductor diodes.
Selenium and copper oxide rectifiers
Main article: Metal rectifier
Once common until replaced by more compact and less costly silicon solid-state rectifiers in the 1970s, these units used stacks of oxide-coated metal plates and took advantage of the semiconductor properties of selenium or copper oxide. While selenium rectifiers were lighter in weight and used less power than comparable vacuum tube rectifiers, they had the disadvantage of finite life expectancy, increasing resistance with age, and were only suitable to use at low frequencies. Both selenium and copper oxide rectifiers have somewhat better tolerance of momentary voltage transients than silicon rectifiers.
Typically these rectifiers were made up of stacks of metal plates or washers, held together by a central bolt, with the number of stacks determined by voltage; each cell was rated for about 20 V. An automotive battery charger rectifier might have only one cell: the high-voltage power supply for a vacuum tube might have dozens of stacked plates. Current density in an air-cooled selenium stack was about 600 mA per square inch of active area (about 90 mA per square centimeter).
Silicon and germanium diodes
Main article: Diode
Silicon diodes are the most widely used rectifiers for lower voltages and powers, and have largely replaced other rectifiers. Due to their substantially lower forward voltage (0.3V versus 0.7V for silicon diodes) germanium diodes have an inherent advantage over silicon diodes in low voltage circuits.
High power: thyristors (SCRs) and newer silicon-based voltage sourced converters
Main article: Silicon controlled rectifier
In high-power applications, from 1975 to 2000, most mercury valve arc-rectifiers were replaced by stacks of very high power thyristors, silicon devices with two extra layers of semiconductor, in comparison to a simple diode.
In medium-power transmission applications, even more complex and sophisticated voltage sourced converter (VSC) silicon semiconductor rectifier systems, such as insulated gate bipolar transistors (IGBT) and gate turn-off thyristors (GTO), have made smaller high voltage DC power transmission systems economical. All of these devices function as rectifiers.
As of 2009 it was expected that these high-power silicon "self-commutating switches", in particular IGBTs and a variant thyristor (related to the GTO) called the integrated gate-commutated thyristor (IGCT), would be scaled-up in power rating to the point that they would eventually replace simple thyristor-based AC rectification systems for the highest power-transmission DC applications.
Active rectifier
Main article: Active rectification
Active rectification is a technique for improving the efficiency of rectification by replacing diodes with actively controlled switches such as transistors, usually power MOSFETs or power BJTs. Whereas normal semiconductor diodes have a roughly fixed voltage drop of around 0.5 to 1 volts, active rectifiers behave as resistances, and can have arbitrarily low voltage drop.
Historically, vibrator-driven switches or motor-driven commutators have also been used for mechanical rectifiers and synchronous rectification.
Active rectification has many applications. It is frequently used for arrays of photovoltaic panels to avoid reverse current flow that can cause overheating with partial shading while giving minimum power loss.
Current research
A major area of research is to develop higher frequency rectifiers, that can rectify into terahertz and light frequencies. These devices are used in optical heterodyne detection, which has myriad applications in optical fiber communication and atomic clocks. Another prospective application for such devices is to directly rectify light waves picked up by tiny antennas, called nantennas, to produce DC electric power. It is thought that arrays of antennas could be a more efficient means of producing solar power than solar cells.
A related area of research is to develop smaller rectifiers, because a smaller device has a higher cutoff frequency. Research projects are attempting to develop a unimolecular rectifier, a single organic molecule that would function as a rectifier.
See also
- AC adapter
- Karl Ferdinand Braun (point-contact rectifier, 1874)
- Precision rectifier
- Rectiformer
- Vienna rectifier
- Warsaw rectifier
References
- Morris, Peter Robin (1990). A History of the World Semiconductor Industry. p. 18. ISBN 978-0-86341-227-1.
- Dushman, S. (1915). "A New Device for Rectifying High Tension Alternating Currents - The Kenotron" General Electric Review pp. 156 - 167. Retrieved Nov. 2021
- Dushman, S. (1915). Electrical Discharge Device. U. S. patent 1,287,265. Retrieved Nov. 2021.
- Lander, Cyril W. (1993). "2. Rectifying Circuits". Power electronics (3rd ed.). London: McGraw-Hill. ISBN 978-0-07-707714-3.
- Williams, B. W. (1992). "Chapter 11". Power electronics : devices, drivers and applications (2nd ed.). Basingstoke: Macmillan. ISBN 978-0-333-57351-8.
- Hendrik Rissik (1941). Mercury-arc current convertors [sic] : an introduction to the theory and practice of vapour-arc discharge devices and to the study of rectification phenomena. Sir I. Pitman & sons, ltd.
- Kimbark, Edward Wilson (1971). Direct current transmission (4. printing. ed.). New York: Wiley-Interscience. pp. 508. ISBN 978-0-471-47580-4.
- Wendy Middleton, Mac E. Van Valkenburg (eds), Reference Data for Engineers: Radio, Electronics, Computer, and Communications, p. 14. 13, Newnes, 2002 ISBN 0-7506-7291-9.
- Rashid, Muhammad (13 January 2011). POWER ELECTRONICS HANDBOOK. Elsevier. p. 153. ISBN 9780123820372.
- Atul P.Godse; U. A. Bakshi (1 January 2008). Elements of Electronics Engineering. Technical Publications. p. 8. ISBN 9788184312928.
- Sinclair, Ian Robertson (1987). "Rectification". Electronics for Electricians and Engineers (illustrated ed.). Industrial Press Inc. p. 151. ISBN 978-0-83111000-0. Retrieved 23 June 2022.
- Smith, Edward H. (2013). "2.3.17. Power supplies". Mechanical Engineer's Reference Book (expanded 12th ed.). Butterworth-Heinemann. p. 2/42. ISBN 978-1-48310257-3. Retrieved 23 June 2022.
- Cartwright, Kenneth; Kaminsky, Edit (2017). "New equations for capacitance vs ripple in power supplies" (PDF). Latin American Journal of Physics Education. 11 (1): 1301–01 1301–11.
- H. P. Westman et al., (ed), Reference Data for Radio Engineers Fifth Edition, 1968, Howard W. Sams pp. 12-14, 12-15, 12-16
- Mansell, A.D.; Shen, J. (1 January 1994). "Pulse converters in traction applications". Power Engineering Journal. 8 (4): 183. doi:10.1049/pe:19940407 (inactive 7 December 2024).
{{cite journal}}: CS1 maint: DOI inactive as of December 2024 (link) - Hawkins, Nehemiah (1914). "54. Rectifiers". Hawkins Electrical Guide: Principles of electricity, magnetism, induction, experiments, dynamo. New York: T. Audel.
- "How To Make An Electrolytic Rectifier". Chestofbooks.com. Retrieved 15 March 2012.
- US patent 1671970, Glenn W. Carpenter, "Liquid Rectifier", issued 1928-06-05
- American Technical Society (1920). Cyclopedia of applied electricity. Vol. 2. American technical society. p. 487.
- Pictures of a mercury-arc rectifier in operation can be seen here: Belsize Park deep shelter rectifier 1, Belsize Park deep shelter rectifier 2
- Sood, Vijay K (31 May 2004). HVDC and FACTS Controllers: Applications of Static Converters in Power Systems. Springer-Verlag. p. 1. ISBN 978-1-4020-7890-3.
The first 25 years of HVDC transmission were sustained by converters having mercury arc valves till the mid-1970s. The next 25 years till the year 2000 were sustained by line-commutated converters using thyristor valves. It is predicted that the next 25 years will be dominated by force-commutated converters . Initially, this new force-commutated era has commenced with Capacitor Commutated Converters (CCC) eventually to be replaced by self-commutated converters due to the economic availability of high-power switching devices with their superior characteristics.
- H. P. Westman et al., (ed), Reference Data for Radio Engineers, Fifth Edition, 1968, Howard W. Sams and Co., no ISBN, Library of Congress Card No. 43-14665 chapter 13
- Arrillaga, Jos; Liu, Yonghe H; Watson, Neville R; Murray, Nicholas J (12 January 2010). Self-Commutating Converters for High Power Applications. John Wiley & Sons. ISBN 978-0-470-68212-8.
- Ali Emadi (2009). Integrated power electronic converters and digital control. CRC Press. pp. 145–146. ISBN 978-1-4398-0069-0.
-
Maurice Agnus Oudin (1907). Standard polyphase apparatus and systems (5th ed.). Van Nostrand. p. 236.
synchronous rectifier commutator.
- Idaho National Laboratory (2007). "Harvesting the sun's energy with antennas". Retrieved 3 October 2008.



 of this three-pulse DC voltage are calculated from the RMS value
of this three-pulse DC voltage are calculated from the RMS value  of the input phase voltage (line to neutral voltage, 120 V in North America, 230 V within Europe at mains operation):
of the input phase voltage (line to neutral voltage, 120 V in North America, 230 V within Europe at mains operation):  . The average no-load output voltage
. The average no-load output voltage  results from the
results from the  (from 30° to 150°):
(from 30° to 150°):

 (from 60° to 120°) with the peak value
(from 60° to 120°) with the peak value  :
:


 amounts 1/4 of the peak value of the phase input voltage
amounts 1/4 of the peak value of the phase input voltage 





 (the divisors are 2 rather than √2 because no power is delivered on the negative half-cycle)
(the divisors are 2 rather than √2 because no power is delivered on the negative half-cycle)









 rating of the transformer can be defined as:
rating of the transformer can be defined as: 

 times the RMS voltage (unloaded) for a capacitor input filter. Offsetting this is superior voltage regulation and higher available current, which reduce peak voltage and ripple current demands on power supply components. Inductors require
times the RMS voltage (unloaded) for a capacitor input filter. Offsetting this is superior voltage regulation and higher available current, which reduce peak voltage and ripple current demands on power supply components. Inductors require