Misplaced Pages

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Regular grid" – news · newspapers · books · scholar · JSTOR (December 2009) (Learn how and when to remove this message)

A regular grid is a tessellation of n-dimensional Euclidean space by congruent parallelotopes (e.g. bricks). Its opposite is irregular grid.

Grids of this type appear on graph paper and may be used in finite element analysis, finite volume methods, finite difference methods, and in general for discretization of parameter spaces. Since the derivatives of field variables can be conveniently expressed as finite differences, structured grids mainly appear in finite difference methods. Unstructured grids offer more flexibility than structured grids and hence are very useful in finite element and finite volume methods.

Each cell in the grid can be addressed by index (i, j) in two dimensions or (i, j, k) in three dimensions, and each vertex has coordinates ${\displaystyle (i\cdot dx,j\cdot dy)}$ in 2D or ${\displaystyle (i\cdot dx,j\cdot dy,k\cdot dz)}$ in 3D for some real numbers dx, dy, and dz representing the grid spacing.

Related grids

A Cartesian grid is a special case where the elements are unit squares or unit cubes, and the vertices are points on the integer lattice.

A rectilinear grid is a tessellation by rectangles or rectangular cuboids (also known as rectangular parallelepipeds) that are not, in general, all congruent to each other. The cells may still be indexed by integers as above, but the mapping from indexes to vertex coordinates is less uniform than in a regular grid. An example of a rectilinear grid that is not regular appears on logarithmic scale graph paper.

A skewed grid is a tessellation of parallelograms or parallelepipeds. (If the unit lengths are all equal, it is a tessellation of rhombi or rhombohedra.)

A curvilinear grid or structured grid is a grid with the same combinatorial structure as a regular grid, in which the cells are quadrilaterals or cuboids, rather than rectangles or rectangular cuboids.

• 3-D Cartesian grid
• 3-D rectilinear grid
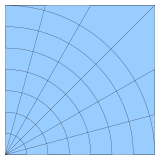• 2-D curvilinear grid
• Non-curvilinear combination of different 2-D curvilinear grids
• 2-D triangular grid.

See also

• Cartesian coordinate system – Most common coordinate system (geometry)
• Integer lattice – Lattice group in Euclidean space whose points are integer n-tuples
• Unstructured grid – Unstructured (or irregular) grid is a tessellation of a part of the Euclidean plane
• Discretization – Conversion of continuous functions into discrete counterparts

References

1. Uznanski, Dan. "Grid". From MathWorld--A Wolfram Web Resource, created by Eric W. Weisstein. Retrieved 25 March 2012.
2. J.F. Thompson, B. K . Soni & N.P. Weatherill (1998). Handbook of Grid Generation. CRC-Press. ISBN 978-0-8493-2687-5.

v t e Tessellation
Periodic Pythagorean Rhombille Schwarz triangle Rectangle Domino Uniform tiling and honeycomb Coloring Convex Kisrhombille Wallpaper group Wythoff
Aperiodic Ammann–Beenker Aperiodic set of prototiles List Einstein problem Socolar–Taylor Gilbert Penrose Pinwheel Quaquaversal Rep-tile and Self-tiling Sphinx Socolar Truchet
Other Anisohedral and Isohedral Architectonic and catoptric Circle Limit III Computer graphics Honeycomb Isotoxal List Packing Pentagonal Problems Domino Wang Heesch's Squaring Dividing a square into similar rectangles Prototile Conway criterion Girih Regular Division of the Plane Regular grid Substitution Voronoi Voderberg
By vertex type Spherical 2 3.n V3.n 4.n V4.n Regular 2 3 4 6 Semi- regular 3.4.3.4 V3.4.3.4 3.4 3.∞ 3.6 V3.6 3.4.6.4 (3.6) 3.12 4.∞ 4.6.12 4.8 Hyper- bolic 3.4.3.5 3.4.3.6 3.4.3.7 3.4.3.8 3.4.3.∞ 3.5.3.5 3.5.3.6 3.6.3.6 3.6.3.8 3.7.3.7 3.8.3.8 3.4.3.4 3.∞.3.∞ 3.7 3.8 3.∞ 3.4 3 3 3 (3.4) (3.4) 3.4.6.4 3.4.7.4 3.4.8.4 3.4.∞.4 3.6.4.6 (3.7) (3.8) 3.14 3.16 3.∞ 4.5.4 4.6.4 4.7.4 4.8.4 4.∞.4 4 4 4 4 4 (4.5) (4.6) 4.6.12 4.6.14 V4.6.14 4.6.16 V4.6.16 4.6.∞ (4.7) (4.8) 4.8.10 V4.8.10 4.8.12 4.8.14 4.8.16 4.8.∞ 4.10 4.10.12 4.12 4.12.16 4.14 4.16 4.∞ 5 5 5 5 5.4.6.4 (5.6) 5.8 5.10 5.12 6 6 6 6 6.4.8.4 (6.8) 6.8 6.10 6.12 6.16 7 7 7 7.6 7.8 7.14 8 8 8 8 8.6 8.12 8.16 ∞ ∞ ∞ ∞ ∞.6 ∞.8

This elementary geometry-related article is a stub. You can help Misplaced Pages by expanding it.

• v
• t
• e

• Tessellation
• Lattice points
• Mesh generation
• Elementary geometry stubs