Misplaced Pages

Redescending M-estimator

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (September 2010) (Learn how and when to remove this message)

In statistics, redescending M-estimators are Ψ-type M-estimators which have ψ functions that are non-decreasing near the origin, but decreasing toward 0 far from the origin. Their ψ functions can be chosen to redescend smoothly to zero, so that they usually satisfy ψ(x) = 0 for all x with |x| > r, where r is referred to as the minimum rejection point.

Due to these properties of the ψ function, these kinds of estimators are very efficient, have a high breakdown point and, unlike other outlier rejection techniques, they do not suffer from a masking effect. They are efficient because they completely reject gross outliers, and do not completely ignore moderately large outliers (like median).

Advantages

Redescending M-estimators have high breakdown points (close to 0.5), and their Ψ function can be chosen to redescend smoothly to 0. This means that moderately large outliers are not ignored completely, and greatly improves the efficiency of the redescending M-estimator.

The redescending M-estimators are slightly more efficient than the Huber estimator for several symmetric, wider tailed distributions, but about 20% more efficient than the Huber estimator for the Cauchy distribution. This is because they completely reject gross outliers, while the Huber estimator effectively treats these the same as moderate outliers.

As other M-estimators, but unlike other outlier rejection techniques, they do not suffer from masking effects.

Disadvantages

The M-estimating equation for a redescending estimator may not have a unique solution. Consequently, the initial point for an iterative solution must be chosen with care, e.g., by use of another estimator.

Choosing redescending Ψ functions

When choosing a redescending Ψ function, care must be taken such that it does not descend too steeply, which may have a very bad influence on the denominator in the expression for the asymptotic variance

∫ Ψ 2 d F ( ∫ Ψ ′ d F ) 2 {\displaystyle {\frac {\int \Psi ^{2}\,dF}{(\int \Psi '\,dF)^{2}}}}

where F is the mixture model distribution.

This effect is particularly harmful when a large negative value of ψ′(x) combines with a large positive value of ψ(x), and there is a cluster of outliers near x.

Examples

1. Hampel's three-part M estimators have Ψ functions which are odd functions and defined for any x by:

Ψ ( x ) = { x , 0 ≤ | x | ≤ a  (central segment) a sign ⁡ ( x ) , a ≤ | x | ≤ b  (high and low flat segments) a ( r − | x | ) r − b sign ⁡ ( x ) , b ≤ | x | ≤ r  (end slopes) 0 , r ≤ | x | (left and right tails) {\displaystyle \Psi (x)={\begin{cases}x,&0\leq |x|\leq a{\text{ (central segment)}}\\a\,\operatorname {sign} (x),&a\leq |x|\leq b{\text{ (high and low flat segments)}}\\{\frac {a(r-|x|)}{r-b}}\,\operatorname {sign} (x),&b\leq |x|\leq r{\text{ (end slopes)}}\\0,&r\leq |x|\qquad \,{\text{(left and right tails)}}\end{cases}}}

This function is plotted in the following figure for a = 1.645, b = 3 and r = 6.5.

2. Tukey's biweight or bisquare M estimators have Ψ functions for any positive k, which defined by:

Ψ ( x ) = x ( 1 − ( x / k ) 2 ) 2 ;   | x | ≤ k {\displaystyle \Psi (x)=x(1-(x/k)^{2})^{2};\ |x|\leq k}

This function is plotted in the following figure for k = 5.

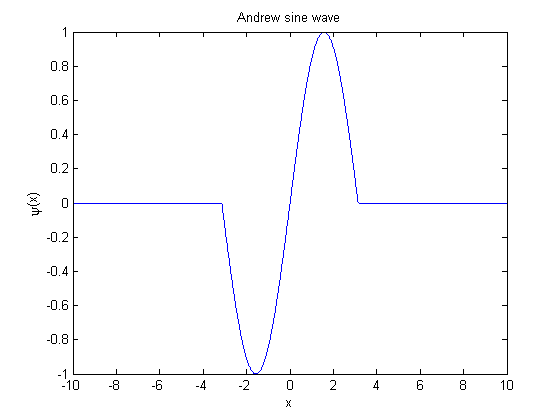
3. Andrew's sine wave M estimator has the following Ψ function:

Ψ ( x ) = sin ⁡ ( x ) ;   − π ≤ x ≤ π {\displaystyle \Psi (x)=\sin {(x)};\ -\pi \leq x\leq \pi }

This function is plotted in the following figure.

References

  • Redescending M-estimators, Shevlyakov, G, Morgenthaler, S and Shurygin, A. M., J Stat Plann Inference 138:2906–2917, 2008.
  • Robust Estimation and Testing, Robert G. Staudte and Simon J. Sheather, Wiley 1990.
  • Robust Statistics, Huber, P., New York: Wiley, 1981.

See also

Categories: