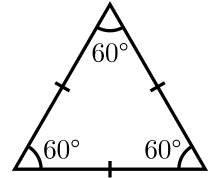
| Equilateral triangle | |
|---|---|
 | |
| Type | Regular polygon |
| Edges and vertices | 3 |
| Schläfli symbol | {3} |
| Coxeter–Dynkin diagrams | |
| Symmetry group | |
| Area | |
| Internal angle (degrees) | 60° |
An equilateral triangle is a triangle in which all three sides have the same length, and all three angles are equal. Because of these properties, the equilateral triangle is a regular polygon, occasionally known as the regular triangle. It is the special case of an isosceles triangle by modern definition, creating more special properties.
The equilateral triangle can be found in various tilings, and in polyhedrons such as the deltahedron and antiprism. It appears in real life in popular culture, architecture, and the study of stereochemistry resembling the molecular known as the trigonal planar molecular geometry.
Properties
An equilateral triangle is a triangle that has three equal sides. It is a special case of an isosceles triangle in the modern definition, stating that an isosceles triangle is defined at least as having two equal sides. Based on the modern definition, this leads to an equilateral triangle in which one of the three sides may be considered its base.
The follow-up definition above may result in more precise properties. For example, since the perimeter of an isosceles triangle is the sum of its two legs and base, the equilateral triangle is formulated as three times its side. The internal angle of an equilateral triangle are equal, 60°. Because of these properties, the equilateral triangles are regular polygons. The cevians of an equilateral triangle are all equal in length, resulting in the median and angle bisector being equal in length, considering those lines as their altitude depending on the base's choice. When the equilateral triangle is flipped across its altitude or rotated around its center for one-third of a full turn, its appearance is unchanged; it has the symmetry of a dihedral group of order six. Other properties are discussed below.
Area

The area of an equilateral triangle with edge length is The formula may be derived from the formula of an isosceles triangle by Pythagoras theorem: the altitude of a triangle is the square root of the difference of squares of a side and half of a base. Since the base and the legs are equal, the height is: In general, the area of a triangle is half the product of its base and height. The formula of the area of an equilateral triangle can be obtained by substituting the altitude formula. Another way to prove the area of an equilateral triangle is by using the trigonometric function. The area of a triangle is formulated as the half product of base and height and the sine of an angle. Because all of the angles of an equilateral triangle are 60°, the formula is as desired.
A version of the isoperimetric inequality for triangles states that the triangle of greatest area among all those with a given perimeter is equilateral. That is, for perimeter and area , the equality holds for the equilateral triangle:
Relationship with circles
The radius of the circumscribed circle is: and the radius of the inscribed circle is half of the circumradius:
The theorem of Euler states that the distance between circumradius and inradius is formulated as . As a corollary of this, the equilateral triangle has the smallest ratio of the circumradius to the inradius of any triangle. That is:
Pompeiu's theorem states that, if is an arbitrary point in the plane of an equilateral triangle but not on its circumcircle, then there exists a triangle with sides of lengths , , and . That is, , , and satisfy the triangle inequality that the sum of any two of them is greater than the third. If is on the circumcircle then the sum of the two smaller ones equals the longest and the triangle has degenerated into a line, this case is known as Van Schooten's theorem.
A packing problem asks the objective of circles packing into the smallest possible equilateral triangle. The optimal solutions show that can be packed into the equilateral triangle, but the open conjectures expand to .
Other mathematical properties

Morley's trisector theorem states that, in any triangle, the three points of intersection of the adjacent angle trisectors form an equilateral triangle.
Viviani's theorem states that, for any interior point in an equilateral triangle with distances , , and from the sides and altitude , independent of the location of .
An equilateral triangle may have integer sides with three rational angles as measured in degrees, known for the only acute triangle that is similar to its orthic triangle (with vertices at the feet of the altitudes), and the only triangle whose Steiner inellipse is a circle (specifically, the incircle). The triangle of the largest area of all those inscribed in a given circle is equilateral, and the triangle of the smallest area of all those circumscribed around a given circle is also equilateral. It is the only regular polygon aside from the square that can be inscribed inside any other regular polygon.
Given a point in the interior of an equilateral triangle, the ratio of the sum of its distances from the vertices to the sum of its distances from the sides is greater than or equal to 2, equality holding when is the centroid. In no other triangle is there a point for which this ratio is as small as 2. This is the Erdős–Mordell inequality; a stronger variant of it is Barrow's inequality, which replaces the perpendicular distances to the sides with the distances from to the points where the angle bisectors of , , and cross the sides (, , and being the vertices). There are numerous other triangle inequalities that hold equality if and only if the triangle is equilateral.
Construction

The equilateral triangle can be constructed in different ways by using circles. The first proposition in the Elements first book by Euclid. Start by drawing a circle with a certain radius, placing the point of the compass on the circle, and drawing another circle with the same radius; the two circles will intersect in two points. An equilateral triangle can be constructed by taking the two centers of the circles and the points of intersection.
An alternative way to construct an equilateral triangle is by using Fermat prime. A Fermat prime is a prime number of the form wherein denotes the non-negative integer, and there are five known Fermat primes: 3, 5, 17, 257, 65537. A regular polygon is constructible by compass and straightedge if and only if the odd prime factors of its number of sides are distinct Fermat primes. To do so geometrically, draw a straight line and place the point of the compass on one end of the line, then swing an arc from that point to the other point of the line segment; repeat with the other side of the line, which connects the point where the two arcs intersect with each end of the line segment in the aftermath.
If three equilateral triangles are constructed on the sides of an arbitrary triangle, either all outward or inward, by Napoleon's theorem the centers of those equilateral triangles themselves form an equilateral triangle.
Appearances
In other related figures
 The equilateral triangle tiling fills the plane
The equilateral triangle tiling fills the plane The Sierpiński triangle
The Sierpiński triangle
Notably, the equilateral triangle tiles the Euclidean plane with six triangles meeting at a vertex; the dual of this tessellation is the hexagonal tiling. Truncated hexagonal tiling, rhombitrihexagonal tiling, trihexagonal tiling, snub square tiling, and snub hexagonal tiling are all semi-regular tessellations constructed with equilateral triangles. Other two-dimensional objects built from equilateral triangles include the Sierpiński triangle (a fractal shape constructed from an equilateral triangle by subdividing recursively into smaller equilateral triangles) and Reuleaux triangle (a curved triangle with constant width, constructed from an equilateral triangle by rounding each of its sides).
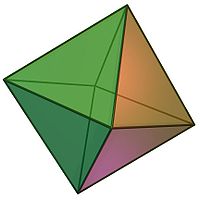
Equilateral triangles may also form a polyhedron in three dimensions. A polyhedron whose faces are all equilateral triangles is called a deltahedron. There are eight strictly convex deltahedra: three of the five Platonic solids (regular tetrahedron, regular octahedron, and regular icosahedron) and five of the 92 Johnson solids (triangular bipyramid, pentagonal bipyramid, snub disphenoid, triaugmented triangular prism, and gyroelongated square bipyramid). More generally, all Johnson solids have equilateral triangles among their faces, though most also have other other regular polygons.
The antiprisms are a family of polyhedra incorporating a band of alternating triangles. When the antiprism is uniform, its bases are regular and all triangular faces are equilateral.
As a generalization, the equilateral triangle belongs to the infinite family of -simplexes, with .
Applications

Equilateral triangles have frequently appeared in man-made constructions and in popular culture. In architecture, an example can be seen in the cross-section of the Gateway Arch and the surface of the Vegreville egg. It appears in the flag of Nicaragua and the flag of the Philippines. It is a shape of a variety of road signs, including the yield sign.
The equilateral triangle occurs in the study of stereochemistry. It can be described as the molecular geometry in which one atom in the center connects three other atoms in a plane, known as the trigonal planar molecular geometry.
In the Thomson problem, concerning the minimum-energy configuration of charged particles on a sphere, and for the Tammes problem of constructing a spherical code maximizing the smallest distance among the points, the best solution known for places the points at the vertices of an equilateral triangle, inscribed in the sphere. This configuration is proven optimal for the Tammes problem, but a rigorous solution to this instance of the Thomson problem is unknown.
See also
References
Notes
- Stahl (2003), p. 37.
- Lardner (1840), p. 46.
- ^ Harris & Stocker (1998), p. 78.
- Cerin (2004), See Theorem 1.
- ^ Owen, Felix & Deirdre (2010), p. 36, 39.
- Carstensen, Fine & Rosenberger (2011), p. 156.
- ^ McMullin & Parkinson (1936), p. 96.
- Chakerian (1979).
- Svrtan & Veljan (2012).
- Alsina & Nelsen (2010), p. 102–103.
- Melissen & Schuur (1995).
- Posamentier & Salkind (1996).
- Conway & Guy (1996), p. 201, 228–229.
- Bankoff & Garfunkel (1973), p. 19.
- Dörrie (1965), p. 379–380.
- Lee (2001).
- Cromwell (1997), p. 62.
- Křížek, Luca & Somer (2001), p. 1–2.
- Grünbaum & Shepard (1977).
- Alsina & Nelsen (2010), p. 102–103.
- Trigg (1978).
- Berman (1971).
- Horiyama et al. (2015), p. 124.
- Coxeter (1948), p. 120–121.
- Pelkonen & Albrecht (2006), p. 160.
- Alsina & Nelsen (2015), p. 22.
- White & Calderón (2008), p. 3.
- Guillermo (2012), p. 161.
- Riley, Cochran & Ballard (1982).
- Petrucci, Harwood & Herring (2002), p. 413–414, See Table 11.1.
- Whyte (1952).
Works cited
- Alsina, Claudi; Nelsen, Roger B. (2010). Charming Proofs: A Journey Into Elegant Mathematics. Mathematical Association of America. ISBN 9780883853481.
- ———; ——— (2015). A Mathematical Space Odyssey: Solid Geometry in the 21st Century. Vol. 50. Mathematical Association of America. ISBN 978-1-61444-216-5.
- Bankoff, Leon; Garfunkel, Jack (January 1973). "The heptagonal triangle". Mathematics Magazine. 46 (1): 7–19. doi:10.1080/0025570X.1973.11976267.
- Berman, Martin (1971). "Regular-faced convex polyhedra". Journal of the Franklin Institute. 291 (5): 329–352. doi:10.1016/0016-0032(71)90071-8. MR 0290245.
- Cerin, Zvonko (2004). "The vertex-midpoint-centroid triangles" (PDF). Forum Geometricorum. 4: 97–109.
- Carstensen, Celine; Fine, Celine; Rosenberger, Gerhard (2011). Abstract Algebra: Applications to Galois Theory, Algebraic Geometry and Cryptography. De Gruyter. p. 156. ISBN 978-3-11-025009-1.
- Chakerian, G. D. (1979). "Chapter 7: A Distorted View of Geometry". In Honsberger, R. (ed.). Mathematical Plums. Washington DC: Mathematical Association of America. p. 147.
- Conway, J. H.; Guy, R. K. (1996). The Book of Numbers. Springer-Verlag.
- Coxeter, H. S. M. Coxeter (1948). Regular Polytopes (1 ed.). London: Methuen & Co. LTD. OCLC 4766401. Zbl 0031.06502.
- Cromwell, Peter R. (1997). Polyhedra. Cambridge University Press. ISBN 978-0-521-55432-9.
- Dörrie, Heinrich (1965). 100 Great Problems of Elementary Mathematics. Dover Publications.
- Grünbaum, Branko; Shepard, Geoffrey (November 1977). "Tilings by Regular Polygons" (PDF). Mathematics Magazine. 50 (5). Taylor & Francis, Ltd.: 231–234. doi:10.2307/2689529. JSTOR 2689529. MR 1567647. S2CID 123776612. Zbl 0385.51006. Archived from the original (PDF) on 2016-03-03. Retrieved 2023-03-09.
- Guillermo, Artemio R. (2012). Historical Dictionary of the Philippines. Scarecrow Press. ISBN 978-0810872462.
- Harris, John W.; Stocker, Horst (1998). Handbook of mathematics and computational science. New York: Springer-Verlag. doi:10.1007/978-1-4612-5317-4 (inactive 1 November 2024). ISBN 0-387-94746-9. MR 1621531.
{{cite book}}: CS1 maint: DOI inactive as of November 2024 (link) - Herz-Fischler, Roger (2000). The Shape of the Great Pyramid. Wilfrid Laurier University Press. ISBN 0-88920-324-5.
- Horiyama, Takayama; Itoh, Jin-ichi; Katoh, Naoi; Kobayashi, Yuki; Nara, Chie (14–16 September 2015). "Continuous Folding of Regular Dodecahedra". In Akiyama, Jin; Ito, Hiro; Sakai, Toshinori; Uno, Yushi (eds.). Discrete and Computational Geometry and Graphs. Japanese Conference on Discrete and Computational Geometry and Graphs. Kyoto. doi:10.1007/978-3-319-48532-4. ISBN 978-3-319-48532-4. ISSN 1611-3349.
- Křížek, Michal; Luca, Florian; Somer, Lawrence (2001). 17 Lectures on Fermat Numbers: From Number Theory to Geometry. CMS Books in Mathematics. Vol. 9. New York: Springer-Verlag. doi:10.1007/978-0-387-21850-2. ISBN 978-0-387-95332-8. MR 1866957.
- Lardner, Dionysius (1840). A Treatise on Geometry and Its Application in the Arts. London: The Cabinet Cyclopædia.
- Lee, Hojoo (2001). "Another proof of the Erdős–Mordell Theorem" (PDF). Forum Geometricorum. 1: 7–8. Archived from the original (PDF) on 2023-06-16. Retrieved 2012-05-02.
- McMullin, Daniel; Parkinson, Albert Charles (1936). An Introduction to Engineering Mathematics. Vol. 1. Cambridge University Press.
- Melissen, J. B. M.; Schuur, P. C. (1995). "Packing 16, 17 or 18 circles in an equilateral triangle". Discrete Mathematics. 145 (1–3): 333–342. doi:10.1016/0012-365X(95)90139-C. MR 1356610.
- Owen, Byer; Felix, Lazebnik; Deirdre, Smeltzer (2010). Methods for Euclidean Geometry. Classroom Resource Materials. Vol. 37. Washington, D.C.: Mathematical Association of America. doi:10.5860/choice.48-3331. ISBN 9780883857632. OCLC 501976971. S2CID 118179744.
- Pelkonen, Eeva-Liisa; Albrecht, Donald, eds. (2006). Eero Saarinen: Shaping the Future. Yale University Press. pp. 160, 224, 226. ISBN 978-0972488129.
{{cite book}}: CS1 maint: ref duplicates default (link) - Petrucci, R. H.; Harwood, W. S.; Herring, F. G. (2002). General Chemistry: Principles and Modern Applications (8th ed.). Prentice Hall. ISBN 978-0-13-014329-7.
- Posamentier, Alfred S.; Salkind, Charles T. (1996). Challenging Problems in Geometry. Dover Publications.
- Riley, Michael W.; Cochran, David J.; Ballard, John L. (December 1982). "An Investigation of Preferred Shapes for Warning Labels". Human Factors: The Journal of the Human Factors and Ergonomics Society. 24 (6): 737–742. doi:10.1177/001872088202400610. S2CID 109362577.
- Stahl, Saul (2003). Geometry from Euclid to Knots. Prentice-Hall. ISBN 0-13-032927-4.
- Svrtan, Dragutin; Veljan, Darko (2012). "Non-Euclidean versions of some classical triangle inequalities". Forum Geometricorum. 12: 197–209.
- Trigg, Charles W. (1978). "An infinite class of deltahedra". Mathematics Magazine. 51 (1): 55–57. doi:10.1080/0025570X.1978.11976675. JSTOR 2689647. MR 1572246.
- White, Steven F.; Calderón, Esthela (2008). Culture and Customs of Nicaragua. Greenwood Press. ISBN 978-0313339943.
- Whyte, L. L. (1952). "Unique arrangements of points on a sphere". The American Mathematical Monthly. 59 (9): 606–611. doi:10.1080/00029890.1952.11988207. JSTOR 2306764. MR 0050303.
External links
| Fundamental convex regular and uniform polytopes in dimensions 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform polychoron | Pentachoron | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||
| Polygons (List) | |||||||
|---|---|---|---|---|---|---|---|
| Triangles | |||||||
| Quadrilaterals | |||||||
| By number of sides |
| ||||||
| Star polygons | |||||||
| Classes | |||||||


 has a height of
has a height of  , the sine of 60°.
, the sine of 60°. is
is
 The formula may be derived from the formula of an isosceles triangle by
The formula may be derived from the formula of an isosceles triangle by  of a triangle is
of a triangle is  In general, the area of a triangle is half the product of its base and height. The formula of the area of an equilateral triangle can be obtained by substituting the altitude formula. Another way to prove the area of an equilateral triangle is by using the
In general, the area of a triangle is half the product of its base and height. The formula of the area of an equilateral triangle can be obtained by substituting the altitude formula. Another way to prove the area of an equilateral triangle is by using the  and area
and area  , the equality holds for the equilateral triangle:
, the equality holds for the equilateral triangle:

 and the radius of the
and the radius of the 
 between circumradius and inradius is formulated as
between circumradius and inradius is formulated as  . As a corollary of this, the equilateral triangle has the smallest ratio of the circumradius
. As a corollary of this, the equilateral triangle has the smallest ratio of the circumradius  to the inradius
to the inradius  of any triangle. That is:
of any triangle. That is:

 is an arbitrary point in the plane of an equilateral triangle
is an arbitrary point in the plane of an equilateral triangle  but not on its
but not on its  ,
,  , and
, and  . That is,
. That is,  circles packing into the smallest possible equilateral triangle
circles packing into the smallest possible equilateral triangle that can be packed into the equilateral triangle, but the open conjectures expand to
that can be packed into the equilateral triangle, but the open conjectures expand to  .
.
 ,
,  , and
, and  from the sides and altitude
from the sides and altitude  independent of the location of
independent of the location of  ,
,  , and
, and  cross the sides (
cross the sides ( ,
,  , and
, and  being the vertices). There are numerous other
being the vertices). There are numerous other  wherein
wherein  denotes the
denotes the  .
.
 places the points at the vertices of an equilateral triangle,
places the points at the vertices of an equilateral triangle,