| It has been suggested that Draft:Tau (mathematical constant) be merged into this article. (Discuss) Proposed since July 2024. |
| Turn | |
|---|---|
 Counterclockwise rotations about the center point starting from the right, where a complete rotation corresponds to an angle of rotation of 1 turn. Counterclockwise rotations about the center point starting from the right, where a complete rotation corresponds to an angle of rotation of 1 turn. | |
| General information | |
| Unit of | Plane angle |
| Symbol | tr, pla, rev, cyc |
| Conversions | |
| 1 tr in ... | ... is equal to ... |
| radians | 2π rad ≈ 6.283185307... rad |
| milliradians | 2000π mrad ≈ 6283.185307... mrad |
| degrees | 360° |
| gradians | 400 |
The turn (symbol tr or pla) is a unit of plane angle measurement that is the measure of a complete angle—the angle subtended by a complete circle at its center. One turn is equal to 2π radians, 360 degrees or 400 gradians. As an angular unit, one turn also corresponds to one cycle (symbol cyc or c) or to one revolution (symbol rev or r). Common related units of frequency are cycles per second (cps) and revolutions per minute (rpm). The angular unit of the turn is useful in connection with, among other things, electromagnetic coils (e.g., transformers), rotating objects, and the winding number of curves. Divisions of a turn include the half-turn and quarter-turn, spanning a straight angle and a right angle, respectively; metric prefixes can also be used as in, e.g., centiturns (ctr), milliturns (mtr), etc.
Because one turn is radians, some have proposed representing 2π with a single letter. In 2010, Michael Hartl proposed using the Greek letter (tau), equal to the ratio of a circle's circumference to its radius () and corresponding to one turn, for greater conceptual simplicity when stating angles in radians. This proposal did not initially gain widespread acceptance in the mathematical community, but the constant has become more widespread, having been added to several major programming languages and calculators.
In the ISQ, an arbitrary "number of turns" (also known as "number of revolutions" or "number of cycles") is formalized as a dimensionless quantity called rotation, defined as the ratio of a given angle and a full turn. It is represented by the symbol N. (See below for the formula.)
Unit symbols
There are several unit symbols for the turn.
EU and Switzerland
The German standard DIN 1315 (March 1974) proposed the unit symbol "pla" (from Latin: plenus angulus 'full angle') for turns. Covered in DIN 1301-1 [de] (October 2010), the so-called Vollwinkel ('full angle') is not an SI unit. However, it is a legal unit of measurement in the EU and Switzerland.
Calculators
The scientific calculators HP 39gII and HP Prime support the unit symbol "tr" for turns since 2011 and 2013, respectively. Support for "tr" was also added to newRPL for the HP 50g in 2016, and for the hp 39g+, HP 49g+, HP 39gs, and HP 40gs in 2017. An angular mode TURN was suggested for the WP 43S as well, but the calculator instead implements "MULπ" (multiples of π) as mode and unit since 2019.
Divisions
See also: Angle § UnitsMany angle units are defined as a division of the turn. For example, the degree is defined such that one turn is 360 degrees.
Using metric prefixes, the turn can be divided in 100 centiturns or 1000 milliturns, with each milliturn corresponding to an angle of 0.36°, which can also be written as 21′ 36″. A protractor divided in centiturns is normally called a "percentage protractor". While percentage protractors have existed since 1922, the terms centiturns, milliturns and microturns were introduced much later by the British astronomer Fred Hoyle in 1962. Some measurement devices for artillery and satellite watching carry milliturn scales.
Binary fractions of a turn are also used. Sailors have traditionally divided a turn into 32 compass points, which implicitly have an angular separation of 1/32 turn. The binary degree, also known as the binary radian (or brad), is 1/256 turn. The binary degree is used in computing so that an angle can be represented to the maximum possible precision in a single byte. Other measures of angle used in computing may be based on dividing one whole turn into 2 equal parts for other values of n.
Proposals for a single letter to represent 2π
See also: Pi § Adoption of the symbol π
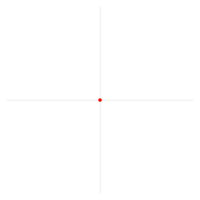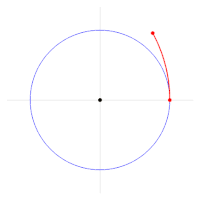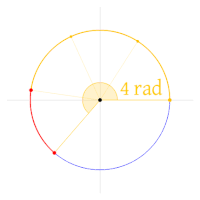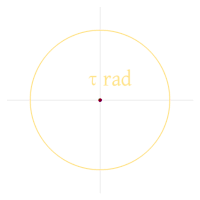


The number 2π (approximately 6.28) is the ratio of a circle's circumference to its radius, and the number of radians in one turn.
The meaning of the symbol was not originally fixed to the ratio of the circumference and the diameter. In 1697, David Gregory used π/ρ (pi over rho) to denote the perimeter of a circle (i.e., the circumference) divided by its radius. However, earlier in 1647, William Oughtred had used δ/π (delta over pi) for the ratio of the diameter to perimeter. The first use of the symbol π on its own with its present meaning (of perimeter divided by diameter) was in 1706 by the Welsh mathematician William Jones.
The first known usage of a single letter to denote the 6.28... constant was in Leonhard Euler's 1727 Essay Explaining the Properties of Air, where it was denoted by the letter π. Euler would later use the letter π for the 3.14... constant in his 1736 Mechanica and 1748 Introductio in analysin infinitorum, though defined as half the circumference of a circle of radius 1—a unit circle—rather than the ratio of circumference to diameter. Elsewhere in Introductio in analysin infinitorum, Euler instead used the letter π for one-fourth of the circumference of a unit circle, or 1.57... . Usage of the letter π, sometimes for 3.14... and other times for 6.28..., became widespread, with the definition varying as late as 1761; afterward, π was standardized as being equal to 3.14... .
Several people have independently proposed using 𝜏 = 2π, including:
- Joseph Lindenburg (c. 1990)
- John Fisher (2004)
- Peter Harremoës (2010)
- Michael Hartl (2010)
In 2001, Robert Palais proposed using the number of radians in a turn as the fundamental circle constant instead of π, which amounts to the number of radians in half a turn, in order to make mathematics simpler and more intuitive. His proposal used a "π with three legs" symbol to denote the constant ().
In 2008, Robert P. Crease proposed the idea of defining a constant as the ratio of circumference to radius, a proposal supported by John Horton Conway. Crease used the Greek letter psi: .
The same year, Thomas Colignatus proposed the uppercase Greek letter theta, Θ, to represent 2π. The Greek letter theta derives from the Phoenician and Hebrew letter teth, 𐤈 or ט, and it has been observed that the older version of the symbol, which means wheel, resembles a wheel with four spokes. It has also been proposed to use the wheel symbol, teth, to represent the value 2π, and more recently a connection has been made among other ancient cultures on the existence of a wheel, sun, circle, or disk symbol—i.e. other variations of teth—as representation for 2π.
In 2010, Michael Hartl proposed to use the Greek letter tau to represent the circle constant: τ = 2π. He offered several reasons for the choice of constant, primarily that it allows fractions of a turn to be expressed more directly: for instance, a 3/4 turn would be represented as 3τ/4 rad instead of 3π/2 rad. As for the choice of notation, he offered two reasons. First, τ is the number of radians in one turn, and both τ and turn begin with a /t/ sound. Second, τ visually resembles π, whose association with the circle constant is unavoidable. Hartl's Tau Manifesto gives many examples of formulas that are asserted to be clearer where τ is used instead of π. For example, Hartl asserts that replacing Euler's identity e = −1 by e = 1 (which Hartl also calls "Euler's identity") is more fundamental and meaningful. He also claims that the formula for circular area in terms of τ, A = 1/2𝜏r, contains a natural factor of 1/2 arising from integration.
Initially, this proposal did not receive significant acceptance by the mathematical and scientific communities. However, the use of τ has become more widespread. For example:
- In 2012, the educational website Khan Academy began accepting answers expressed in terms of τ.
- The constant τ is made available in the Google calculator, Desmos graphing calculator and in several programming languages such as Python, Raku, Processing, Nim, Rust, GDScript, UE Blueprints, Java, .NET, Odin, and Julia. Support is upcoming in Liberty Eiffel.
- It has been used in at least one mathematical research article, authored by the τ promoter Peter Harremoës.
- The iPhone's Convert Angle option expresses the turn as τ.
The following table shows how various identities appear when τ = 2π is used instead of π. For a more complete list, see List of formulae involving π.
| Formula | Using π | Using τ | Notes |
|---|---|---|---|
| Angle subtended by 1/4 of a circle | τ/4 rad = 1/4 turn | ||
| Circumference of a circle | The length of an arc of angle θ is L = θr. | ||
| Area of a circle | The area of a sector of angle θ is A = 1/2θr. | ||
| Area of a regular n-gon with unit circumradius | |||
| n-ball and n-sphere volume recurrence relation |
|
|
V0(r) = 1 S0(r) = 2 |
| Cauchy's integral formula | is the boundary of a disk containing in the complex plane. | ||
| Standard normal distribution | |||
| Stirling's approximation | |||
| nth roots of unity | |||
| Planck constant | ħ is the reduced Planck constant. | ||
| Angular frequency |
In culture
𝜏 has made numerous appearances in culture. It is celebrated annually on June 28, known as Tau Day. 𝜏 has been covered in videos by Vi Hart, Numberphile, SciShow, Steve Mould, Khan Academy, and 3Blue1Brown, and it has appeared in the comics xkcd, Saturday Morning Breakfast Cereal, and Sally Forth. The Massachusetts Institute of Technology usually announces admissions on March 14 at 6:28 p.m., which is on Pi Day at Tau Time.
Unit conversion

One turn is equal to 2π (≈ 6.283185307179586) radians, 360 degrees, or 400 gradians.
| Turns | Radians | Degrees | Gradians | |
|---|---|---|---|---|
| 0 turn | 0 rad | 0° | 0 | |
| 1/72 turn | 𝜏/72 rad | π/36 rad | 5° | 5+5/9 |
| 1/24 turn | 𝜏/24 rad | π/12 rad | 15° | 16+2/3 |
| 1/16 turn | 𝜏/16 rad | π/8 rad | 22.5° | 25 |
| 1/12 turn | 𝜏/12 rad | π/6 rad | 30° | 33+1/3 |
| 1/10 turn | 𝜏/10 rad | π/5 rad | 36° | 40 |
| 1/8 turn | 𝜏/8 rad | π/4 rad | 45° | 50 |
| 1/2π turn | 1 rad | c. 57.3° | c. 63.7 | |
| 1/6 turn | 𝜏/6 rad | π/3 rad | 60° | 66+2/3 |
| 1/5 turn | 𝜏/5 rad | 2π/5 rad | 72° | 80 |
| 1/4 turn | 𝜏/4 rad | π/2 rad | 90° | 100 |
| 1/3 turn | 𝜏/3 rad | 2π/3 rad | 120° | 133+1/3 |
| 2/5 turn | 2𝜏/5 rad | 4π/5 rad | 144° | 160 |
| 1/2 turn | 𝜏/2 rad | π rad | 180° | 200 |
| 3/4 turn | 3𝜏/4 rad | 3π/2 rad | 270° | 300 |
| 1 turn | 𝜏 rad | 2π rad | 360° | 400 |
In the ISQ/SI
| Rotation | |
|---|---|
| Other names | number of revolutions, number of cycles, number of turns, number of rotations |
| Common symbols | N |
| SI unit | Unitless |
| Dimension | 1 |
In the International System of Quantities (ISQ), rotation (symbol N) is a physical quantity defined as number of revolutions:
N is the number (not necessarily an integer) of revolutions, for example, of a rotating body about a given axis. Its value is given by:
where 𝜑 denotes the measure of rotational displacement.
The above definition is part of the ISQ, formalized in the international standard ISO 80000-3 (Space and time), and adopted in the International System of Units (SI).
Rotation count or number of revolutions is a quantity of dimension one, resulting from a ratio of angular displacement. It can be negative and also greater than 1 in modulus. The relationship between quantity rotation, N, and unit turns, tr, can be expressed as:
where {𝜑}tr is the numerical value of the angle 𝜑 in units of turns (see Physical quantity § Components).
In the ISQ/SI, rotation is used to derive rotational frequency (the rate of change of rotation with respect to time), denoted by n:
The SI unit of rotational frequency is the reciprocal second (s). Common related units of frequency are hertz (Hz), cycles per second (cps), and revolutions per minute (rpm).
| Revolution | |
|---|---|
| Unit of | Rotation |
| Symbol | rev, r, cyc, c |
| Conversions | |
| 1 rev in ... | ... is equal to ... |
| Base units | 1 |
The superseded version ISO 80000-3:2006 defined "revolution" as a special name for the dimensionless unit "one", which also received other special names, such as the radian. Despite their dimensional homogeneity, these two specially named dimensionless units are applicable for non-comparable kinds of quantity: rotation and angle, respectively. "Cycle" is also mentioned in ISO 80000-3, in the definition of period.
In programming languages
The following table documents various programming languages that have implemented the circle constant for converting between turns and radians. All of the languages below support the name "Tau" in some casing, but Processing also supports "TWO_PI" and Raku also supports the symbol "τ" for accessing the same value.
| Language | Identifiers | First Version | Year Released |
|---|---|---|---|
| C# / .NET | System.Math.Tau and System.MathF.Tau | 5.0 | 2020 |
| Crystal | TAU | 0.36.0 | 2021 |
| Eiffel | math_constants.Tau | Curtiss | Not yet released |
| GDScript | TAU | Godot 3.0 | 2018 |
| Java | Math.TAU | 19 | 2022 |
| Nim | TAU | 0.14.0 | 2016 |
| Processing | TAU and TWO_PI | 2.0 | 2013 |
| Python | math.tau | 3.6 | 2016 |
| Raku | tau and τ | ||
| Rust | std::f64::consts::TAU | 1.47.0 | 2020 |
| Zig | std.math.tau | 0.6.0 | 2019 |
See also
- Ampere-turn
- Hertz (modern) or Cycle per second (older)
- Angle of rotation
- Revolutions per minute
- Repeating circle
- Spat (angular unit) – the solid angle counterpart of the turn, equivalent to 4π steradians.
- Unit interval
- Divine Proportions: Rational Trigonometry to Universal Geometry
- Modulo operation
- Twist (mathematics)
Notes
- The angular unit terms "cycles" and "revolutions" are also used, ambiguously, as shorter versions of the related frequency units.
- Original version, current version
- "The special name revolution, symbol r, for this unit is widely used in specifications on rotating machines."
- "Measurement units of quantities of dimension one are numbers. In some cases, these measurement units are given special names, e.g. radian..."
- "3-14) period duration, period: duration (item 3‑9) of one cycle of a periodic event"
References
- Fitzpatrick, Richard (2021). Newtonian Dynamics: An Introduction. CRC Press. p. 116. ISBN 978-1-000-50953-3. Retrieved 2023-04-25.
- Units & Symbols for Electrical & Electronic Engineers (PDF). London, UK: Institution of Engineering and Technology. 2016. Archived (PDF) from the original on 2023-07-18. Retrieved 2023-07-18. (1+iii+32+1 pages)
- ^ Hartl, Michael (2019-03-14) . "The Tau Manifesto". Archived from the original on 2019-06-28. Retrieved 2013-09-14.
- ^ "Life of pi in no danger – Experts cold-shoulder campaign to replace with tau". Telegraph India. 2011-06-30. Archived from the original on 2013-07-13. Retrieved 2019-08-05.
- ^ McMillan, Robert (2020-03-13). "For Math Fans, Nothing Can Spoil Pi Day—Except Maybe Tau Day". Wall Street Journal. ISSN 0099-9660. Retrieved 2020-05-21.
- German, Sigmar; Drath, Peter (2013-03-13) . Handbuch SI-Einheiten: Definition, Realisierung, Bewahrung und Weitergabe der SI-Einheiten, Grundlagen der Präzisionsmeßtechnik (in German) (1 ed.). Friedrich Vieweg & Sohn Verlagsgesellschaft mbH, reprint: Springer-Verlag. p. 421. ISBN 978-3-32283606-9. 978-3-528-08441-7, 978-3-32283606-9. Retrieved 2015-08-14.
- Kurzweil, Peter (2013-03-09) . Das Vieweg Einheiten-Lexikon: Formeln und Begriffe aus Physik, Chemie und Technik (in German) (1 ed.). Vieweg, reprint: Springer-Verlag. p. 403. doi:10.1007/978-3-322-92920-4. ISBN 978-3-32292920-4. 978-3-322-92921-1. Retrieved 2015-08-14.
- "Richtlinie 80/181/EWG - Richtlinie des Rates vom 20. Dezember 1979 zur Angleichung der Rechtsvorschriften der Mitgliedstaaten über die Einheiten im Meßwesen und zur Aufhebung der Richtlinie 71/354/EWG" (in German). 1980-02-15. Archived from the original on 2019-06-22. Retrieved 2019-08-06.
- "Richtlinie 2009/3/EG des Europäischen Parlaments und des Rates vom 11. März 2009 zur Änderung der Richtlinie 80/181/EWG des Rates zur Angleichung der Rechtsvorschriften der Mitgliedstaaten über die Einheiten im Messwesen (Text von Bedeutung für den EWR)" (in German). 2009-03-11. Archived from the original on 2019-08-06. Retrieved 2019-08-06.
- "Art. 15 Einheiten in Form von nichtdezimalen Vielfachen oder Teilen von SI-Einheiten". Einheitenverordnung (in Swiss High German). Schweizerischer Bundesrat. 1994-11-23. 941.202. Archived from the original on 2019-05-10. Retrieved 2013-01-01.
- Lapilli, Claudio Daniel (2016-05-11). "RE: newRPL: Handling of units". HP Museum. Archived from the original on 2017-08-10. Retrieved 2019-08-05.
- Lapilli, Claudio Daniel (2018-10-25). "Chapter 3: Units - Available Units - Angles". newRPL User Manual. Archived from the original on 2019-08-06. Retrieved 2019-08-07.
- Paul, Matthias R. (2016-01-12) . "RE: WP-32S in 2016?". HP Museum. Archived from the original on 2019-08-05. Retrieved 2019-08-05.
I'd like to see a TURN mode being implemented as well. TURN mode works exactly like DEG, RAD and GRAD (including having a full set of angle unit conversion functions like on the WP 34S), except for that a full circle doesn't equal 360 degree, 6.2831... rad or 400 gon, but 1 turn. (I found it to be really convenient in engineering/programming, where you often have to convert to/from other unit representations But I think it can also be useful for educational purposes. ) Having the angle of a full circle normalized to 1 allows for easier conversions to/from a whole bunch of other angle units
- Bonin, Walter (2019) . WP 43S Owner's Manual (PDF). 0.12 (draft ed.). pp. 72, 118–119, 311. ISBN 978-1-72950098-9. Archived (PDF) from the original on 2023-07-18. Retrieved 2019-08-05. (314 pages)
- Bonin, Walter (2019) . WP 43S Reference Manual (PDF). 0.12 (draft ed.). pp. iii, 54, 97, 128, 144, 193, 195. ISBN 978-1-72950106-1. Archived (PDF) from the original on 2023-07-18. Retrieved 2019-08-05. (271 pages)
- ^ Hoyle, Fred (1962). Chandler, M. H. (ed.). Astronomy (1 ed.). London, UK: Macdonald & Co. (Publishers) Ltd. / Rathbone Books Limited. LCCN 62065943. OCLC 7419446. (320 pages)
- ^ Klein, Herbert Arthur (2012) . "Chapter 8: Keeping Track of Time". The Science of Measurement: A Historical Survey (The World of Measurements: Masterpieces, Mysteries and Muddles of Metrology). Dover Books on Mathematics (corrected reprint of original ed.). Dover Publications, Inc. / Courier Corporation (originally by Simon & Schuster, Inc.). p. 102. ISBN 978-0-48614497-9. LCCN 88-25858. Retrieved 2019-08-06. (736 pages)
- Croxton, Frederick E. (1922). "A Percentage Protractor - Designed for Use in the Construction of Circle Charts or "Pie Diagrams"". Journal of the American Statistical Association. Short Note. 18 (137): 108–109. doi:10.1080/01621459.1922.10502455.
- Schiffner, Friedrich (1965). Wähnl, Maria Emma (ed.). "Bestimmung von Satellitenbahnen". Astronomische Mitteilungen der Urania-Sternwarte Wien (in German). 8. Wien, Austria: Volksbildungshaus Wiener Urania.
- Hayes, Eugene Nelson (1975) . Trackers of the Skies. History of the Smithsonian Satellite-tracking Program. Cambridge, Massachusetts, USA: Academic Press / Howard A. Doyle Publishing Company.
- "ooPIC Programmer's Guide - Chapter 15: URCP". ooPIC Manual & Technical Specifications - ooPIC Compiler Ver 6.0. Savage Innovations, LLC. 2007 . Archived from the original on 2008-06-28. Retrieved 2019-08-05.
- Hargreaves, Shawn . "Angles, integers, and modulo arithmetic". blogs.msdn.com. Archived from the original on 2019-06-30. Retrieved 2019-08-05.
- Beckmann, Petr (1989) . A History of Pi. Barnes & Noble Publishing.
- Schwartzman, Steven (1994). The Words of Mathematics: An Etymological Dictionary of Mathematical Terms Used in English. The Mathematical Association of America. p. 165. ISBN 978-0-88385511-9.
- Jones, William (1706). Synopsis Palmariorum Matheseos. London: J. Wale. pp. 243, 263. p. 263:
There are various other ways of finding the Lengths, or Areas of particular Curve Lines or Planes, which may very much facilitate the Practice; as for instance, in the Circle, the Diameter is to Circumference as 1 to
Reprinted in Smith, David Eugene (1929). "William Jones: The First Use of π for the Circle Ratio". A Source Book in Mathematics. McGraw–Hill. pp. 346–347.
3.14159, &c. = π. This Series (among others for the same purpose, and drawn from the same Principle) I receiv'd from the Excellent Analyst, and my much Esteem'd Friend Mr. John Machin; and by means thereof, Van Ceulen's Number, or that in Art. 64.38. may be Examin'd with all desireable Ease and Dispatch. - Veling, Anne (2001). "Pi through the ages". veling.nl. Archived from the original on 2009-07-02.
- Euler, Leonhard (1727). "Tentamen explicationis phaenomenorum aeris" (PDF). Commentarii Academiae Scientiarum Imperialis Petropolitana (in Latin). 2: 351. E007. Archived (PDF) from the original on 2016-04-01. Retrieved 2017-10-15.
Sumatur pro ratione radii ad peripheriem, I : π
English translation by Ian Bruce Archived 10 June 2016 at the Wayback Machine: "π is taken for the ratio of the radius to the periphery " - Euler, Leonhard (1747). Henry, Charles (ed.). Lettres inédites d'Euler à d'Alembert. Bullettino di Bibliografia e di Storia delle Scienze Matematiche e Fisiche (in French). Vol. 19 (published 1886). p. 139. E858.
Car, soit π la circonference d'un cercle, dout le rayon est = 1
English translation in Cajori, Florian (1913). "History of the Exponential and Logarithmic Concepts". The American Mathematical Monthly. 20 (3): 75–84. doi:10.2307/2973441. JSTOR 2973441.Letting π be the circumference (!) of a circle of unit radius
- Euler, Leonhard (1736). "Ch. 3 Prop. 34 Cor. 1". Mechanica sive motus scientia analytice exposita. (cum tabulis) (in Latin). Vol. 1. Academiae scientiarum Petropoli. p. 113. E015.
Denotet 1 : π rationem diametri ad peripheriam
English translation by Ian Bruce Archived 10 June 2016 at the Wayback Machine : "Let 1 : π denote the ratio of the diameter to the circumference" - Euler, Leonhard (1707–1783) (1922). Leonhardi Euleri opera omnia. 1, Opera mathematica. Volumen VIII, Leonhardi Euleri introductio in analysin infinitorum. Tomus primus / ediderunt Adolf Krazer et Ferdinand Rudio (in Latin). Lipsae: B.G. Teubneri. pp. 133–134. E101. Archived from the original on 2017-10-16. Retrieved 2017-10-15.
{{cite book}}: CS1 maint: numeric names: authors list (link) - Segner, Johann Andreas von (1761). Cursus Mathematicus: Elementorum Analyseos Infinitorum Elementorum Analyseos Infinitorvm (in Latin). Renger. p. 374.
Si autem π notet peripheriam circuli, cuius diameter eſt 2
- "Pi". Encyclopaedia Brittanica. 2024-03-14. Retrieved 2024-03-26.
- Euler, Leonhard (1746). Nova theoria lucis et colorum. Opuscula varii argumenti (in Latin). sumtibus Ambr. Haude & Jo. Carol. Speneri, bibliop. p. 200.
unde constat punctum B per datum tantum spatium de loco fuo naturali depelli, ad quam maximam distantiam pertinget, elapso tempore t=π/m denotante π angulum 180°, quo fit cos(mt)=- 1 & B b=2α.
[from which it is clear that the point B is pushed by a given distance from its natural position, and it will reach the maximum distance after the elapsed time t=π/m, π denoting an angle of 180°, which becomes cos(mt)=- 1 & B b=2α.] - sudgylacmoe; Hartl, Michael (2023-06-28). The Tau Manifesto - With Michael Hartl (YouTube video). Information shown at 18:35. Retrieved 2024-07-24.
- ^ Palais, Robert (2001). "Pi is Wrong" (PDF). The Mathematical Intelligencer. 23 (3). New York, USA: Springer-Verlag: 7–8. doi:10.1007/bf03026846. S2CID 120965049. Archived (PDF) from the original on 2019-07-18. Retrieved 2019-08-05.
- Crease, Robert (2008-02-01). "Constant failure". Physics World. Institute of Physics. Retrieved 2024-08-03.
- Cool, Thomas "Colignatus" (2008-07-18) . "Trig rerigged. Trigonometry reconsidered. Measuring angles in 'unit meter around' and using the unit radius functions Xur and Yur" (PDF). Archived from the original (PDF) on 2023-07-18. Retrieved 2023-07-18. (18 pages)
- Mann, Steve; Janzen, Ryan E.; Ali, Mir Adnan; Scourboutakos, Pete; Guleria, Nitin (22–24 October 2014). "Integral Kinematics (Time-Integrals of Distance, Energy, etc.) and Integral Kinesiology". Proceedings of the 2014 IEEE GEM. Toronto, Ontario, Canada: 627–629. S2CID 6462220. Retrieved 2023-07-18.
- Mann, Steve; Chen, Hongyu; Aylward, Graeme; Jorritsma, Megan; Mann, Christina; Defaz Poveda, Diego David; Pierce, Cayden; Lam, Derek; Stairs, Jeremy; Hermandez, Jesse; Li, Qiushi; Xiang, Yi Xin; Kanaan, Georges (June 2019). "Eye Itself as a Camera: Sensors, Integrity, and Trust". The 5th ACM Workshop on Wearable Systems and Applications (Keynote): 1–2. doi:10.1145/3325424.3330210. S2CID 189926593. Retrieved 2023-07-18.
- Hartl, Michael (2010-03-14). "The Tau Manifesto" (PDF). Archived (PDF) from the original on 2019-07-18. Retrieved 2019-08-05.
- Aron, Jacob (2011-01-08). "Michael Hartl: It's time to kill off pi". New Scientist. Interview. 209 (2794): 23. Bibcode:2011NewSc.209...23A. doi:10.1016/S0262-4079(11)60036-5.
- Landau, Elizabeth (2011-03-14). "On Pi Day, is 'pi' under attack?". cnn.com. CNN. Archived from the original on 2018-12-19. Retrieved 2019-08-05.
- Bartholomew, Randyn Charles (2014-06-25). "Let's Use Tau--It's Easier Than Pi - A growing movement argues that killing pi would make mathematics simpler, easier and even more beautiful". Scientific American. Archived from the original on 2019-06-18. Retrieved 2015-03-20.
- "Happy Tau Day!". blog.khanacademy.org. 2012-06-28. Archived from the original on 2023-07-18. Retrieved 2020-12-19.
- "Supported Functions". help.desmos.com. Archived from the original on 2023-03-26. Retrieved 2023-03-21.
- Coghlan, Nick (2017-02-25). "PEP 628 -- Add math.tau". Python.org. Archived from the original on 2019-07-22. Retrieved 2019-08-05.
- "math — Mathematical functions". Python 3.7.0 documentation. Archived from the original on 2019-07-29. Retrieved 2019-08-05.
- "Perl 6 terms". Archived from the original on 2019-07-22. Retrieved 2019-08-05.
- "TAU". Processing. Archived from the original on 2019-07-22. Retrieved 2019-08-05.
- "math". Nim. Archived from the original on 2019-07-22. Retrieved 2019-08-05.
- "std::f64::consts::TAU - Rust". doc.rust-lang.org. Archived from the original on 2023-07-18. Retrieved 2020-10-09.
- "Constants @GDScript - Godot Engine (stable) documentation in English". Godot Docs.
- "Get TAU - Unreal Engine 5.2 Documentation". Unreal Engine Docs.
- Darcy, Joe. "JDK-8283136: Add constant for tau to Math and StrictMath". bugs.openjdk.org.
- "Math class". Java 19 documentation.
- John-H-K. "Add Math.Tau Pull Request #37517 · dotnet/Runtime". GitHub.
- "Math.Tau Field". .NET Reference Documentation.
- "package math - pkg.odin-lang.org". Odin documentation.
- "JuliaMath / Tau.jl". GitHub. Retrieved 2024-11-24.
- "Release Notes (Versions history)". Liberty Eiffel. Retrieved 2024-11-17.
- Harremoës, Peter (2017). "Bounds on tail probabilities for negative binomial distributions". Kybernetika. 52 (6): 943–966. arXiv:1601.05179. doi:10.14736/kyb-2016-6-0943. S2CID 119126029.
- Harremoës, Peter (2018-11-17). "Al-Kashi's constant τ" (PDF). Archived (PDF) from the original on 2019-07-22. Retrieved 2018-09-20.
- Naumovski, Jovana (2022-08-05). "iOS 16 Has a Hidden Unit Converter for Temperatures, Time Zones, Distance, and Other Measurements". Gadget Hacks. Retrieved 2024-10-21.
- Abbott, Stephen (April 2012). "My Conversion to Tauism" (PDF). Math Horizons. 19 (4): 34. doi:10.4169/mathhorizons.19.4.34. S2CID 126179022. Archived (PDF) from the original on 2013-09-28.
- Hartl, Michael. "Tau Day". Retrieved 2024-11-01.
- Hart, Vi. "Pi is (still) Wrong". YouTube. Retrieved 2024-11-01.
- Hart, Vi. "A Song About A Circle Constant". YouTube. Retrieved 2024-11-01.
- Hart, Vi. "360 Video for Tau Day". YouTube. Retrieved 2024-11-01.
- Haran, Brady; Moriarty, Phil. "Tau replaces Pi - Numberphile". YouTube. Retrieved 2024-11-01.
- Haran, Brady; Moriarty, Phil. "Tau of Phi - Numberphile". YouTube. Retrieved 2024-11-01.
- Haran, Brady; Mould, Steve; Parker, Matthew. "Tau vs Pi Smackdown - Numberphile". YouTube. Retrieved 2024-11-01.
- Hofmeister, Caitlin. "Happy Tau Day!". YouTube. Retrieved 2024-11-01.
- Mould, Steve (2018-11-06). Stand-up comedy routine about bad science. Event occurs at 10:31. Retrieved 2024-11-17.
- Mould, Steve (2023-11-06). A cast saw on human skin. Event occurs at 7:22. Retrieved 2024-11-13.
- Mould, Steve (2024-03-14). world record calculation of tau by hand. Retrieved 2024-11-13.
- Khan, Sal (2011-07-11). Tau versus pi | Graphs of trig functions | Trigonometry | Khan Academy. Retrieved 2024-11-24.
- Sanderson, Grant (2018-03-14). How pi was almost 6.283185... Retrieved 2024-11-24.
- Sanderson, Grant (2019-07-07). e^(iπ) in 3.14 minutes, using dynamics | DE5. Event occurs at 3:08. Retrieved 2024-11-24.
- Munroe, Randall. "Pi vs. Tau". xkcd. Retrieved 2024-11-01.
- Munroe, Randall. "Symbols". xkcd. Retrieved 2024-11-01.
- Weinersmith, Zachary. "Fresh". Saturday Morning Breakfast Cereal. Retrieved 2024-11-02.
- Weinersmith, Zachary. "Better than Pi". Saturday Morning Breakfast Cereal. Retrieved 2024-11-02.
- Weinersmith, Zachary. "Social". Saturday Morning Breakfast Cereal. Retrieved 2024-11-02.
- Marciuliano, Francesco. "Sally Forth Comic Strip 2018-10-13". Comics Kingdom. Retrieved 2024-11-13.
- "Fun & Culture – MIT Facts". Massachusetts Institute of Technology. Retrieved 2024-11-02.
- Sequence OEIS: A019692
- ^ "ISO 80000-3:2019 Quantities and units — Part 3: Space and time" (2 ed.). International Organization for Standardization. 2019. Retrieved 2019-10-23. (11 pages)
- The International System of Units (PDF) (9th ed.), International Bureau of Weights and Measures, Dec 2022, ISBN 978-92-822-2272-0
- Thompson, Ambler; Taylor, Barry N. (2020-03-04) . "The NIST Guide for the Use of the International System of Units, Special Publication 811" (2008 ed.). National Institute of Standards and Technology. Retrieved 2023-07-17.
- ^ "ISO 80000-3:2006". ISO. 2001-08-31. Retrieved 2023-04-25.
- "ISO 80000-1:2009(en) Quantities and units — Part 1: General". iso.org. Retrieved 2023-05-12.
 radians, some have proposed
radians, some have proposed  (
( was not originally fixed to the ratio of the circumference and the diameter. In 1697,
was not originally fixed to the ratio of the circumference and the diameter. In 1697,  ).
).
 .
.













 is the boundary of a disk containing
is the boundary of a disk containing  in the complex plane.
in the complex plane.













