Misplaced Pages

Rhombohedron

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
(Redirected from Rhombic prism) Polyhedron with six rhombi as faces
Rhombohedron
Rhombohedron
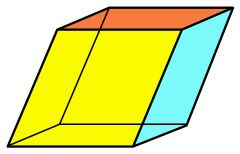
Type prism
Faces 6 rhombi
Edges 12
Vertices 8
Symmetry group Ci , , (×), order 2
Properties convex, equilateral, zonohedron, parallelohedron

In geometry, a rhombohedron (also called a rhombic hexahedron or, inaccurately, a rhomboid) is a special case of a parallelepiped in which all six faces are congruent rhombi. It can be used to define the rhombohedral lattice system, a honeycomb with rhombohedral cells. A rhombohedron has two opposite apices at which all face angles are equal; a prolate rhombohedron has this common angle acute, and an oblate rhombohedron has an obtuse angle at these vertices. A cube is a special case of a rhombohedron with all sides square.

Special cases

The common angle at the two apices is here given as θ {\displaystyle \theta } . There are two general forms of the rhombohedron: oblate (flattened) and prolate (stretched).

Oblate rhombohedron Prolate rhombohedron

In the oblate case θ > 90 ∘ {\displaystyle \theta >90^{\circ }} and in the prolate case θ < 90 ∘ {\displaystyle \theta <90^{\circ }} . For θ = 90 ∘ {\displaystyle \theta =90^{\circ }} the figure is a cube.

Certain proportions of the rhombs give rise to some well-known special cases. These typically occur in both prolate and oblate forms.

Form Cube √2 Rhombohedron Golden Rhombohedron
Angle
constraints 		θ = 90 ∘ {\displaystyle \theta =90^{\circ }}
Ratio of diagonals 1 √2 Golden ratio
Occurrence Regular solid Dissection of the rhombic dodecahedron Dissection of the rhombic triacontahedron

Solid geometry

For a unit (i.e.: with side length 1) rhombohedron, with rhombic acute angle θ   {\displaystyle \theta ~} , with one vertex at the origin (0, 0, 0), and with one edge lying along the x-axis, the three generating vectors are

e1 : ( 1 , 0 , 0 ) , {\displaystyle {\biggl (}1,0,0{\biggr )},}
e2 : ( cos ⁡ θ , sin ⁡ θ , 0 ) , {\displaystyle {\biggl (}\cos \theta ,\sin \theta ,0{\biggr )},}
e3 : ( cos ⁡ θ , cos ⁡ θ − cos 2 ⁡ θ sin ⁡ θ , 1 − 3 cos 2 ⁡ θ + 2 cos 3 ⁡ θ sin ⁡ θ ) . {\displaystyle {\biggl (}\cos \theta ,{\cos \theta -\cos ^{2}\theta \over \sin \theta },{{\sqrt {1-3\cos ^{2}\theta +2\cos ^{3}\theta }} \over \sin \theta }{\biggr )}.}

The other coordinates can be obtained from vector addition of the 3 direction vectors: e1 + e2 , e1 + e3 , e2 + e3 , and e1 + e2 + e3 .

The volume V {\displaystyle V} of a rhombohedron, in terms of its side length a {\displaystyle a} and its rhombic acute angle θ   {\displaystyle \theta ~} , is a simplification of the volume of a parallelepiped, and is given by

V = a 3 ( 1 − cos ⁡ θ ) 1 + 2 cos ⁡ θ = a 3 ( 1 − cos ⁡ θ ) 2 ( 1 + 2 cos ⁡ θ ) = a 3 1 − 3 cos 2 ⁡ θ + 2 cos 3 ⁡ θ   . {\displaystyle V=a^{3}(1-\cos \theta ){\sqrt {1+2\cos \theta }}=a^{3}{\sqrt {(1-\cos \theta )^{2}(1+2\cos \theta )}}=a^{3}{\sqrt {1-3\cos ^{2}\theta +2\cos ^{3}\theta }}~.}

We can express the volume V {\displaystyle V} another way :

V = 2 3   a 3 sin 2 ⁡ ( θ 2 ) 1 − 4 3 sin 2 ⁡ ( θ 2 )   . {\displaystyle V=2{\sqrt {3}}~a^{3}\sin ^{2}\left({\frac {\theta }{2}}\right){\sqrt {1-{\frac {4}{3}}\sin ^{2}\left({\frac {\theta }{2}}\right)}}~.}

As the area of the (rhombic) base is given by a 2 sin ⁡ θ   {\displaystyle a^{2}\sin \theta ~} , and as the height of a rhombohedron is given by its volume divided by the area of its base, the height h {\displaystyle h} of a rhombohedron in terms of its side length a {\displaystyle a} and its rhombic acute angle θ {\displaystyle \theta } is given by

h = a   ( 1 − cos ⁡ θ ) 1 + 2 cos ⁡ θ sin ⁡ θ = a   1 − 3 cos 2 ⁡ θ + 2 cos 3 ⁡ θ sin ⁡ θ   . {\displaystyle h=a~{(1-\cos \theta ){\sqrt {1+2\cos \theta }} \over \sin \theta }=a~{{\sqrt {1-3\cos ^{2}\theta +2\cos ^{3}\theta }} \over \sin \theta }~.}

Note:

h = a   z {\displaystyle h=a~z} 3 , where z {\displaystyle z} 3 is the third coordinate of e3 .

The body diagonal between the acute-angled vertices is the longest. By rotational symmetry about that diagonal, the other three body diagonals, between the three pairs of opposite obtuse-angled vertices, are all the same length.

Relation to orthocentric tetrahedra

Four points forming non-adjacent vertices of a rhombohedron necessarily form the four vertices of an orthocentric tetrahedron, and all orthocentric tetrahedra can be formed in this way.

Rhombohedral lattice

Main article: Rhombohedral lattice

The rhombohedral lattice system has rhombohedral cells, with 6 congruent rhombic faces forming a trigonal trapezohedron:

See also

Notes

  1. More accurately, rhomboid is a two-dimensional figure.

References

  1. Miller, William A. (January 1989). "Maths Resource: Rhombic Dodecahedra Puzzles". Mathematics in School. 18 (1): 18–24. JSTOR 30214564.
  2. Inchbald, Guy (July 1997). "The Archimedean honeycomb duals". The Mathematical Gazette. 81 (491): 213–219. doi:10.2307/3619198. JSTOR 3619198.
  3. Coxeter, HSM. Regular Polytopes. Third Edition. Dover. p.26.
  4. Lines, L (1965). Solid geometry: with chapters on space-lattices, sphere-packs and crystals. Dover Publications.
  5. "Vector Addition". Wolfram. 17 May 2016. Retrieved 17 May 2016.
  6. Court, N. A. (October 1934), "Notes on the orthocentric tetrahedron", American Mathematical Monthly, 41 (8): 499–502, doi:10.2307/2300415, JSTOR 2300415.

External links

Convex polyhedra
Platonic solids (regular)
Archimedean solids
(semiregular or uniform)
Catalan solids
(duals of Archimedean)
Dihedral regular
Dihedral uniform
duals:
Dihedral others
Degenerate polyhedra are in italics.
Categories: