
In economics and finance, risk aversion is the tendency of people to prefer outcomes with low uncertainty to those outcomes with high uncertainty, even if the average outcome of the latter is equal to or higher in monetary value than the more certain outcome.
Risk aversion explains the inclination to agree to a situation with a lower average payoff that is more predictable rather than another situation with a less predictable payoff that is higher on average. For example, a risk-averse investor might choose to put their money into a bank account with a low but guaranteed interest rate, rather than into a stock that may have high expected returns, but also involves a chance of losing value.
Example
 Utility function of a risk-averse (risk-avoiding) individual
Utility function of a risk-averse (risk-avoiding) individual Utility function of a risk-neutral individual
Utility function of a risk-neutral individual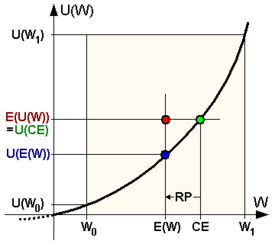 Utility function of a risk-loving (risk-seeking) individualCE – Certainty equivalent; E(U(W)) – Expected value of the utility (expected utility) of the uncertain payment W; E(W) – Expected value of the uncertain payment; U(CE) – Utility of the certainty equivalent; U(E(W)) – Utility of the expected value of the uncertain payment; U(W0) – Utility of the minimal payment; U(W1) – Utility of the maximal payment; W0 – Minimal payment; W1 – Maximal payment; RP – Risk premium
Utility function of a risk-loving (risk-seeking) individualCE – Certainty equivalent; E(U(W)) – Expected value of the utility (expected utility) of the uncertain payment W; E(W) – Expected value of the uncertain payment; U(CE) – Utility of the certainty equivalent; U(E(W)) – Utility of the expected value of the uncertain payment; U(W0) – Utility of the minimal payment; U(W1) – Utility of the maximal payment; W0 – Minimal payment; W1 – Maximal payment; RP – Risk premium
A person is given the choice between two scenarios: one with a guaranteed payoff, and one with a risky payoff with same average value. In the former scenario, the person receives $50. In the uncertain scenario, a coin is flipped to decide whether the person receives $100 or nothing. The expected payoff for both scenarios is $50, meaning that an individual who was insensitive to risk would not care whether they took the guaranteed payment or the gamble. However, individuals may have different risk attitudes.
A person is said to be:
- risk averse (or risk avoiding) - if they would accept a certain payment (certainty equivalent) of less than $50 (for example, $40), rather than taking the gamble and possibly receiving nothing.
- risk neutral – if they are indifferent between the bet and a certain $50 payment.
- risk loving (or risk seeking) – if they would accept the bet even when the guaranteed payment is more than $50 (for example, $60).
The average payoff of the gamble, known as its expected value, is $50. The smallest guaranteed dollar amount that an individual would be indifferent to compared to an uncertain gain of a specific average predicted value is called the certainty equivalent, which is also used as a measure of risk aversion. An individual that is risk averse has a certainty equivalent that is smaller than the prediction of uncertain gains. The risk premium is the difference between the expected value and the certainty equivalent. For risk-averse individuals, risk premium is positive, for risk-neutral persons it is zero, and for risk-loving individuals their risk premium is negative.
Utility of money
In expected utility theory, an agent has a utility function u(c) where c represents the value that he might receive in money or goods (in the above example c could be $0 or $40 or $100).
The utility function u(c) is defined only up to positive affine transformation – in other words, a constant could be added to the value of u(c) for all c, and/or u(c) could be multiplied by a positive constant factor, without affecting the conclusions.
An agent is risk-averse if and only if the utility function is concave. For instance u(0) could be 0, u(100) might be 10, u(40) might be 5, and for comparison u(50) might be 6.
The expected utility of the above bet (with a 50% chance of receiving 100 and a 50% chance of receiving 0) is
- ,
and if the person has the utility function with u(0)=0, u(40)=5, and u(100)=10 then the expected utility of the bet equals 5, which is the same as the known utility of the amount 40. Hence the certainty equivalent is 40.
The risk premium is ($50 minus $40)=$10, or in proportional terms
or 25% (where $50 is the expected value of the risky bet: (). This risk premium means that the person would be willing to sacrifice as much as $10 in expected value in order to achieve perfect certainty about how much money will be received. In other words, the person would be indifferent between the bet and a guarantee of $40, and would prefer anything over $40 to the bet.
In the case of a wealthier individual, the risk of losing $100 would be less significant, and for such small amounts his utility function would be likely to be almost linear. For instance, if u(0) = 0 and u(100) = 10, then u(40) might be 4.02 and u(50) might be 5.01.
The utility function for perceived gains has two key properties: an upward slope, and concavity. (i) The upward slope implies that the person feels that more is better: a larger amount received yields greater utility, and for risky bets the person would prefer a bet which is first-order stochastically dominant over an alternative bet (that is, if the probability mass of the second bet is pushed to the right to form the first bet, then the first bet is preferred). (ii) The concavity of the utility function implies that the person is risk averse: a sure amount would always be preferred over a risky bet having the same expected value; moreover, for risky bets the person would prefer a bet which is a mean-preserving contraction of an alternative bet (that is, if some of the probability mass of the first bet is spread out without altering the mean to form the second bet, then the first bet is preferred).
Measures of risk aversion under expected utility theory
There are various measures of the risk aversion expressed by those given utility function. Several functional forms often used for utility functions are represented by these measures.
Absolute risk aversion
The higher the curvature of , the higher the risk aversion. However, since expected utility functions are not uniquely defined (are defined only up to affine transformations), a measure that stays constant with respect to these transformations is needed rather than just the second derivative of . One such measure is the Arrow–Pratt measure of absolute risk aversion (ARA), after the economists Kenneth Arrow and John W. Pratt, also known as the coefficient of absolute risk aversion, defined as
where and denote the first and second derivatives with respect to of . For example, if so and then Note how does not depend on and so affine transformations of do not change it.
The following expressions relate to this term:
- Exponential utility of the form is unique in exhibiting constant absolute risk aversion (CARA): is constant with respect to c.
- Hyperbolic absolute risk aversion (HARA) is the most general class of utility functions that are usually used in practice (specifically, CRRA (constant relative risk aversion, see below), CARA (constant absolute risk aversion), and quadratic utility all exhibit HARA and are often used because of their mathematical tractability). A utility function exhibits HARA if its absolute risk aversion is a hyperbola, namely
The solution to this differential equation (omitting additive and multiplicative constant terms, which do not affect the behavior implied by the utility function) is:
where and . Note that when , this is CARA, as , and when , this is CRRA (see below), as . See
- Decreasing/increasing absolute risk aversion (DARA/IARA) is present if is decreasing/increasing. Using the above definition of ARA, the following inequality holds for DARA:
and this can hold only if . Therefore, DARA implies that the utility function is positively skewed; that is, . Analogously, IARA can be derived with the opposite directions of inequalities, which permits but does not require a negatively skewed utility function (). An example of a DARA utility function is , with , while , with would represent a quadratic utility function exhibiting IARA.
- Experimental and empirical evidence is mostly consistent with decreasing absolute risk aversion.
- Contrary to what several empirical studies have assumed, wealth is not a good proxy for risk aversion when studying risk sharing in a principal-agent setting. Although is monotonic in wealth under either DARA or IARA and constant in wealth under CARA, tests of contractual risk sharing relying on wealth as a proxy for absolute risk aversion are usually not identified.
Relative risk aversion
The Arrow–Pratt measure of relative risk aversion (RRA) or coefficient of relative risk aversion is defined as
- .
Unlike ARA whose units are in $, RRA is a dimensionless quantity, which allows it to be applied universally. Like for absolute risk aversion, the corresponding terms constant relative risk aversion (CRRA) and decreasing/increasing relative risk aversion (DRRA/IRRA) are used. This measure has the advantage that it is still a valid measure of risk aversion, even if the utility function changes from risk averse to risk loving as c varies, i.e. utility is not strictly convex/concave over all c. A constant RRA implies a decreasing ARA, but the reverse is not always true. As a specific example of constant relative risk aversion, the utility function implies RRA = 1.
In intertemporal choice problems, the elasticity of intertemporal substitution often cannot be disentangled from the coefficient of relative risk aversion. The isoelastic utility function
exhibits constant relative risk aversion with and the elasticity of intertemporal substitution . When using l'Hôpital's rule shows that this simplifies to the case of log utility, u(c) = log c, and the income effect and substitution effect on saving exactly offset.
A time-varying relative risk aversion can be considered.
Implications of increasing/decreasing absolute and relative risk aversion
The most straightforward implications of increasing or decreasing absolute or relative risk aversion, and the ones that motivate a focus on these concepts, occur in the context of forming a portfolio with one risky asset and one risk-free asset. If the person experiences an increase in wealth, he/she will choose to increase (or keep unchanged, or decrease) the number of dollars of the risky asset held in the portfolio if absolute risk aversion is decreasing (or constant, or increasing). Thus economists avoid using utility functions such as the quadratic, which exhibit increasing absolute risk aversion, because they have an unrealistic behavioral implication.
Similarly, if the person experiences an increase in wealth, he/she will choose to increase (or keep unchanged, or decrease) the fraction of the portfolio held in the risky asset if relative risk aversion is decreasing (or constant, or increasing).
In one model in monetary economics, an increase in relative risk aversion increases the impact of households' money holdings on the overall economy. In other words, the more the relative risk aversion increases, the more money demand shocks will impact the economy.
Portfolio theory
In modern portfolio theory, risk aversion is measured as the additional expected reward an investor requires to accept additional risk. If an investor is risk-averse, they will invest in multiple uncertain assets, but only when the predicted return on a portfolio that is uncertain is greater than the predicted return on one that is not uncertain will the investor will prefer the former. Here, the risk-return spectrum is relevant, as it results largely from this type of risk aversion. Here risk is measured as the standard deviation of the return on investment, i.e. the square root of its variance. In advanced portfolio theory, different kinds of risk are taken into consideration. They are measured as the n-th root of the n-th central moment. The symbol used for risk aversion is A or An.
Von Neumann-Morgenstern utility theorem
The von Neumann-Morgenstern utility theorem is another model used to denote how risk aversion influences an actor’s utility function. An extension of the expected utility function, the von Neumann-Morgenstern model includes risk aversion axiomatically rather than as an additional variable.
John von Neumann and Oskar Morgenstern first developed the model in their book Theory of Games and Economic Behaviour. Essentially, von Neumann and Morgenstern hypothesised that individuals seek to maximise their expected utility rather than the expected monetary value of assets. In defining expected utility in this sense, the pair developed a function based on preference relations. As such, if an individual’s preferences satisfy four key axioms, then a utility function based on how they weigh different outcomes can be deduced.
In applying this model to risk aversion, the function can be used to show how an individual’s preferences of wins and losses will influence their expected utility function. For example, if a risk-averse individual with $20,000 in savings is given the option to gamble it for $100,000 with a 30% chance of winning, they may still not take the gamble in fear of losing their savings. This does not make sense using the traditional expected utility model however;
The von Neumann-Morgenstern model can explain this scenario. Based on preference relations, a specific utility can be assigned to both outcomes. Now the function becomes;
For a risk averse person, would equal a value that means that the individual would rather keep their $20,000 in savings than gamble it all to potentially increase their wealth to $100,000. Hence a risk averse individuals’ function would show that;
Limitations of expected utility treatment of risk aversion
Using expected utility theory's approach to risk aversion to analyze small stakes decisions has come under criticism. Matthew Rabin has showed that a risk-averse, expected-utility-maximizing individual who,
from any initial wealth level turns down gambles where she loses $100 or gains $110, each with 50% probability will turn down 50–50 bets of losing $1,000 or gaining any sum of money.
Rabin criticizes this implication of expected utility theory on grounds of implausibility—individuals who are risk averse for small gambles due to diminishing marginal utility would exhibit extreme forms of risk aversion in risky decisions under larger stakes. One solution to the problem observed by Rabin is that proposed by prospect theory and cumulative prospect theory, where outcomes are considered relative to a reference point (usually the status quo), rather than considering only the final wealth.
Another limitation is the reflection effect, which demonstrates the reversing of risk aversion. This effect was first presented by Kahneman and Tversky as a part of the prospect theory, in the behavioral economics domain. The reflection effect is an identified pattern of opposite preferences between negative as opposed to positive prospects: people tend to avoid risk when the gamble is between gains, and to seek risks when the gamble is between losses. For example, most people prefer a certain gain of 3,000 to an 80% chance of a gain of 4,000. When posed the same problem, but for losses, most people prefer an 80% chance of a loss of 4,000 to a certain loss of 3,000.
The reflection effect (as well as the certainty effect) is inconsistent with the expected utility hypothesis. It is assumed that the psychological principle which stands behind this kind of behavior is the overweighting of certainty. Options which are perceived as certain are over-weighted relative to uncertain options. This pattern is an indication of risk-seeking behavior in negative prospects and eliminates other explanations for the certainty effect such as aversion for uncertainty or variability.
The initial findings regarding the reflection effect faced criticism regarding its validity, as it was claimed that there are insufficient evidence to support the effect on the individual level. Subsequently, an extensive investigation revealed its possible limitations, suggesting that the effect is most prevalent when either small or large amounts and extreme probabilities are involved.
Bargaining and risk aversion
Numerous studies have shown that in riskless bargaining scenarios, being risk-averse is disadvantageous. Moreover, opponents will always prefer to play against the most risk-averse person. Based on both the von Neumann-Morgenstern and Nash Game Theory model, a risk-averse person will happily receive a smaller commodity share of the bargain. This is because their utility function concaves hence their utility increases at a decreasing rate while their non-risk averse opponents may increase at a constant or increasing rate. Intuitively, a risk-averse person will hence settle for a smaller share of the bargain as opposed to a risk-neutral or risk-seeking individual.
In the brain
Main article: Risk aversion (psychology)Attitudes towards risk have attracted the interest of the field of neuroeconomics and behavioral economics. A 2009 study by Christopoulos et al. suggested that the activity of a specific brain area (right inferior frontal gyrus) correlates with risk aversion, with more risk averse participants (i.e. those having higher risk premia) also having higher responses to safer options. This result coincides with other studies, that show that neuromodulation of the same area results in participants making more or less risk averse choices, depending on whether the modulation increases or decreases the activity of the target area.
Public understanding and risk in social activities
In the real world, many government agencies, e.g. Health and Safety Executive, are fundamentally risk-averse in their mandate. This often means that they demand (with the power of legal enforcement) that risks be minimized, even at the cost of losing the utility of the risky activity. It is important to consider the opportunity cost when mitigating a risk; the cost of not taking the risky action. Writing laws focused on the risk without the balance of the utility may misrepresent society's goals. The public understanding of risk, which influences political decisions, is an area which has recently been recognised as deserving focus. In 2007 Cambridge University initiated the Winton Professorship of the Public Understanding of Risk, a role described as outreach rather than traditional academic research by the holder, David Spiegelhalter.
Children
Children's services such as schools and playgrounds have become the focus of much risk-averse planning, meaning that children are often prevented from benefiting from activities that they would otherwise have had. Many playgrounds have been fitted with impact-absorbing matting surfaces. However, these are only designed to save children from death in the case of direct falls on their heads and do not achieve their main goals. They are expensive, meaning that less resources are available to benefit users in other ways (such as building a playground closer to the child's home, reducing the risk of a road traffic accident on the way to it), and—some argue—children may attempt more dangerous acts, with confidence in the artificial surface. Shiela Sage, an early years school advisor, observes "Children who are only ever kept in very safe places, are not the ones who are able to solve problems for themselves. Children need to have a certain amount of risk taking ... so they'll know how to get out of situations."
Game shows and investments
One experimental study with student-subject playing the game of the TV show Deal or No Deal finds that people are more risk averse in the limelight than in the anonymity of a typical behavioral laboratory. In the laboratory treatments, subjects made decisions in a standard, computerized laboratory setting as typically employed in behavioral experiments. In the limelight treatments, subjects made their choices in a simulated game show environment, which included a live audience, a game show host, and video cameras. In line with this, studies on investor behavior find that investors trade more and more speculatively after switching from phone-based to online trading and that investors tend to keep their core investments with traditional brokers and use a small fraction of their wealth to speculate online.
The behavioural approach to employment status
The basis of the theory, on the connection between employment status and risk aversion, is the varying income level of individuals. On average higher income earners are less risk averse than lower income earners. In terms of employment the greater the wealth of an individual the less risk averse they can afford to be, and they are more inclined to make the move from a secure job to an entrepreneurial venture. The literature assumes a small increase in income or wealth initiates the transition from employment to entrepreneurship-based decreasing absolute risk aversion (DARA), constant absolute risk aversion (CARA), and increasing absolute risk aversion (IARA) preferences as properties in their utility function. The apportioning risk perspective can also be used to as a factor in the transition of employment status, only if the strength of downside risk aversion exceeds the strength of risk aversion. If using the behavioural approach to model an individual’s decision on their employment status there must be more variables than risk aversion and any absolute risk aversion preferences.
Incentive effects are a factor in the behavioural approach an individual takes in deciding to move from a secure job to entrepreneurship. Non-financial incentives provided by an employer can change the decision to transition into entrepreneurship as the intangible benefits helps to strengthen how risk averse an individual is relative to the strength of downside risk aversion. Utility functions do not equate for such effects and can often screw the estimated behavioural path that an individual takes towards their employment status.
The design of experiments, to determine at what increase of wealth or income would an individual change their employment status from a position of security to more risky ventures, must include flexible utility specifications with salient incentives integrated with risk preferences. The application of relevant experiments can avoid the generalisation of varying individual preferences through the use of this model and its specified utility functions.
See also
- Ambiguity aversion
- Equity premium puzzle
- Investor profile
- Loss aversion
- Marginal utility
- Neuroeconomics
- Optimism bias
- Problem gambling, a contrary behavior
- Prudence in economics and finance
- Risk premium
- St. Petersburg paradox
- Statistical risk
- Uncertainty avoidance, which is different, as uncertainty is not the same as risk
- Utility
References
- ^ Werner, Jan (2008). "Risk Aversion". The New Palgrave Dictionary of Economics. pp. 1–6. doi:10.1057/978-1-349-95121-5_2741-1. ISBN 978-1-349-95121-5.
- Mr Lev Virine; Mr Michael Trumper (28 October 2013). ProjectThink: Why Good Managers Make Poor Project Choices. Gower Publishing, Ltd. ISBN 978-1-4724-0403-9.
- David Hillson; Ruth Murray-Webster (2007). Understanding and Managing Risk Attitude. Gower Publishing, Ltd. ISBN 978-0-566-08798-1.
- Adhikari, Binay Kumar; Agrawal, Anup (June 2016). "Does local religiosity matter for bank risk-taking?". Journal of Corporate Finance. 38: 272–293. doi:10.1016/j.jcorpfin.2016.01.009.
- ^ Arrow, K. J. (1965). "Aspects of the Theory of Risk Bearing". The Theory of Risk Aversion. Helsinki: Yrjo Jahnssonin Saatio. Reprinted in: Essays in the Theory of Risk Bearing, Markham Publ. Co., Chicago, 1971, 90–109.
- ^ Pratt, John W. (January 1964). "Risk Aversion in the Small and in the Large". Econometrica. 32 (1/2): 122–136. doi:10.2307/1913738. JSTOR 1913738.
- "Zender's lecture notes".
- Levy, Haim (2006). Stochastic Dominance: Investment Decision Making under Uncertainty (2nd ed.). New York: Springer. ISBN 978-0-387-29302-8.
- Friend, Irwin; Blume, Marshall (1975). "The Demand for Risky Assets". American Economic Review. 65 (5): 900–922. JSTOR 1806628.
- Bellemare, Marc F.; Brown, Zachary S. (January 2010). "On the (Mis)Use of Wealth as a Proxy for Risk Aversion". American Journal of Agricultural Economics. 92 (1): 273–282. doi:10.1093/ajae/aap006. hdl:10161/7006. S2CID 59290774.
- Simon, Carl and Lawrence Blume (2006). Mathematics for Economists (Student ed.). Viva Norton. p. 363. ISBN 978-81-309-1600-2.
- Benchimol, Jonathan (March 2014). "Risk aversion in the Eurozone". Research in Economics. 68 (1): 39–56. doi:10.1016/j.rie.2013.11.005. S2CID 153856059.
- Benchimol, Jonathan; Fourçans, André (March 2012). "Money and risk in a DSGE framework: A Bayesian application to the Eurozone". Journal of Macroeconomics. 34 (1): 95–111. doi:10.1016/j.jmacro.2011.10.003. S2CID 153669907.
- ^ von Neumann, John; Morgenstern, Oskar; Rubinstein, Ariel (1944). Theory of Games and Economic Behavior (60th Anniversary Commemorative ed.). Princeton University Press. ISBN 978-0-691-13061-3. JSTOR j.ctt1r2gkx.
- Gerber, Anke (2020). "The Nash Solution as a von Neumann–Morgenstern Utility Function on Bargaining Games". Homo Oeconomicus. 37 (1–2): 87–104. doi:10.1007/s41412-020-00095-9. hdl:10419/288817. ISSN 0943-0180. S2CID 256553112.
- Prokop, Darren (2023). "Von Neumann–Morgenstern utility function | Definition & Facts | Britannica". www.britannica.com. Retrieved 2023-04-24.
- Rabin, Matthew (2000). "Risk Aversion and Expected-Utility Theory: A Calibration Theorem". Econometrica. 68 (5): 1281–1292. CiteSeerX 10.1.1.295.4269. doi:10.1111/1468-0262.00158. S2CID 16418792.
- ^ Kahneman, Daniel; Tversky, Amos (March 1979). "Prospect Theory: An Analysis of Decision under Risk". Econometrica. 47 (2): 263. CiteSeerX 10.1.1.407.1910. doi:10.2307/1914185. JSTOR 1914185.
- Hershey, John C.; Schoemaker, Paul J.H. (June 1980). "Prospect theory's reflection hypothesis: A critical examination". Organizational Behavior and Human Performance. 25 (3): 395–418. doi:10.1016/0030-5073(80)90037-9.
- Battalio, RaymondC.; Kagel, JohnH.; Jiranyakul, Komain (March 1990). "Testing between alternative models of choice under uncertainty: Some initial results". Journal of Risk and Uncertainty. 3 (1). doi:10.1007/BF00213259. S2CID 154386816.
- Roth, Alvin E.; Rothblum, Uriel G. (1982). "Risk Aversion and Nash's Solution for Bargaining Games with Risky Outcomes". Econometrica. 50 (3): 639–647. doi:10.2307/1912605. ISSN 0012-9682. JSTOR 1912605.
- Murnighan, J. Keith; Roth, Alvin E.; Schoumaker, Francoise (1988). "Risk Aversion in Bargaining: An Experimental Study". Journal of Risk and Uncertainty. 1 (1): 101–124. doi:10.1007/BF00055566. ISSN 0895-5646. JSTOR 41760532. S2CID 154784555.
- Kannai, Yakar (1977-03-01). "Concavifiability and constructions of concave utility functions". Journal of Mathematical Economics. 4 (1): 1–56. doi:10.1016/0304-4068(77)90015-5. ISSN 0304-4068.
- ^ Knoch, Daria; Gianotti, Lorena R. R.; Pascual-Leone, Alvaro; Treyer, Valerie; Regard, Marianne; Hohmann, Martin; Brugger, Peter (14 June 2006). "Disruption of Right Prefrontal Cortex by Low-Frequency Repetitive Transcranial Magnetic Stimulation Induces Risk-Taking Behavior". The Journal of Neuroscience. 26 (24): 6469–6472. doi:10.1523/JNEUROSCI.0804-06.2006. PMC 6674035. PMID 16775134.
- Fecteau, Shirley; Pascual-Leone, Alvaro; Zald, David H.; Liguori, Paola; Théoret, Hugo; Boggio, Paulo S.; Fregni, Felipe (6 June 2007). "Activation of Prefrontal Cortex by Transcranial Direct Current Stimulation Reduces Appetite for Risk during Ambiguous Decision Making". The Journal of Neuroscience. 27 (23): 6212–6218. doi:10.1523/JNEUROSCI.0314-07.2007. PMC 6672163. PMID 17553993.
- Spiegelhalter, David (2009). "Don's Diary" (PDF). CAM – the Cambridge Alumni Magazine. 58. The University of Cambridge Development Office: 3. Archived from the original (PDF) on March 9, 2013.
- Gill, Tim (2007). No fear: Growing up in a Risk Averse society (PDF). Calouste Gulbenkian Foundation. p. 81. ISBN 9781903080085. Archived from the original (PDF) on 2009-03-06.
- Sue Durant, Sheila Sage (10 January 2006). Early Years – The Outdoor Environment. Teachers TV.
- Baltussen, Guido; van den Assem, Martijn J.; van Dolder, Dennie (May 2016). "Risky Choice in the Limelight". Review of Economics and Statistics. 98 (2): 318–332. doi:10.1162/REST_a_00505. S2CID 57561510. SSRN 2057134.
- Barber, Brad M; Odean, Terrance (1 February 2001). "The Internet and the Investor". Journal of Economic Perspectives. 15 (1): 41–54. doi:10.1257/jep.15.1.41.
- Barber, Brad; Odean, Terrance (2002). "Online Investors: Do the Slow Die First?". Review of Financial Studies. 15 (2): 455–488. CiteSeerX 10.1.1.46.6569. doi:10.1093/rfs/15.2.455.
- Konana, Prabhudev; Balasubramanian, Sridhar (May 2005). "The Social–Economic–Psychological model of technology adoption and usage: an application to online investing". Decision Support Systems. 39 (3): 505–524. doi:10.1016/j.dss.2003.12.003.
- ^ Bonilla, Claudio (2021). "Risk aversion, downside risk aversion, and the transition to entrepreneurship". Theory and Decision. 91: 123–133. doi:10.1007/s11238-020-09786-w. S2CID 228879460.
- ^ Harrison, Glenn (2006). "Risk Aversion and Incentive Effects: Comment". The American Economic Review. 95 (3): 897–901. doi:10.1257/0002828054201378 – via The University of Queensland.
U.Sankar (1971), A Utility Function for Wealth for a Risk Averter, Journal of Economic Theory.
External links
- Zevelev, Albert A. (3 February 2014). "Closed Form Solutions in Economics". SSRN 2354226.
{{cite journal}}: Cite journal requires|journal=(help) - Rabin, Matthew (2000). "Diminishing Marginal Utility of Wealth Cannot Explain Risk Aversion". In Kahneman, Daniel; Tversky, Amos (eds.). Choices, Values, and Frames. Cambridge University Press. pp. 202–208. ISBN 978-0-521-62749-8.
- "Monkey business-sense". The Economist. 23 June 2005.
- Arrow-Pratt Measure on About.com:Economics
- Doody, Ryan (2023). "Risk-taking and Tie-breaking" (PDF). Philosophical Studies. 180 (7): 2079–2104. doi:10.1007/s11098-023-01947-1. S2CID 198977278.
- Blackburn, Douglas W.; Ukhov, Andrey (1 May 2008). "Individual vs. Aggregate Preferences: The Case of a Small Fish in a Big Pond". SSRN 941126.
{{cite journal}}: Cite journal requires|journal=(help) - The benefit of utilities: a plausible explanation for small risky parts in the portfolio
 ,
,
 ). This risk premium means that the person would be willing to sacrifice as much as $10 in expected value in order to achieve perfect certainty about how much money will be received. In other words, the person would be indifferent between the bet and a guarantee of $40, and would prefer anything over $40 to the bet.
). This risk premium means that the person would be willing to sacrifice as much as $10 in expected value in order to achieve perfect certainty about how much money will be received. In other words, the person would be indifferent between the bet and a guarantee of $40, and would prefer anything over $40 to the bet.
 , the higher the risk aversion. However, since expected utility functions are not uniquely defined (are defined only up to
, the higher the risk aversion. However, since expected utility functions are not uniquely defined (are defined only up to 
 and
and  denote the first and second derivatives with respect to
denote the first and second derivatives with respect to  of
of  so
so  and
and  then
then  Note how
Note how  does not depend on
does not depend on  and
and  so affine transformations of
so affine transformations of  is unique in exhibiting constant absolute risk aversion (CARA):
is unique in exhibiting constant absolute risk aversion (CARA):  is constant with respect to c.
is constant with respect to c.

 and
and  .
Note that when
.
Note that when  , this is CARA, as
, this is CARA, as  , and when
, and when  , this is CRRA (see below), as
, this is CRRA (see below), as  .
See
.
See

 . Therefore, DARA implies that the utility function is positively skewed; that is,
. Therefore, DARA implies that the utility function is positively skewed; that is,  ). An example of a DARA utility function is
). An example of a DARA utility function is  , with
, with  , while
, while 
 , with
, with  would represent a quadratic utility function exhibiting IARA.
would represent a quadratic utility function exhibiting IARA.
 .
.
 and the elasticity of intertemporal substitution
and the elasticity of intertemporal substitution  . When
. When  using
using 




 can be assigned to both outcomes. Now the function becomes;
can be assigned to both outcomes. Now the function becomes;

