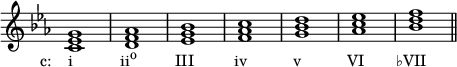The chord progression vi–ii–V–I in the key of C major. Using lead sheet chord names, these chords could be referred to as A minor, D minor, G major and C major.
The chord progression vi–ii–V–I in the key of C major. Using lead sheet chord names, these chords could be referred to as A minor, D minor, G major and C major.In music theory, Roman numeral analysis is a type of harmonic analysis in which chords are represented by Roman numerals, which encode the chord's degree and harmonic function within a given musical key.
Specific notation conventions vary: some theorists use uppercase numerals (e.g. I, IV, V) to represent major chords, and lowercase numerals (e.g. ii, iii, vi) to represent minor chords. Others use uppercase numerals for all chords regardless of their quality. (As the II, III, and VI chords always are minor chords and the VII always diminished, a further distinguishment is thought unneeded, see table for Major Diatonic scale below)
Roman numerals can be used to notate and analyze the harmonic progression of a composition independent of its specific key. For example, the ubiquitous twelve-bar blues progression uses the tonic (I), subdominant (IV), and dominant (V) chords built upon the first, fourth and fifth scale degrees respectively.
History

Roman numeral analysis is based on the idea that chords can be represented and named by one of their notes, their root (see History of the Root (chord) article for more information). The system came about initially from the work and writings of Rameau's fundamental bass.
The earliest usage of Roman numerals may be found in the first volume of Johann Kirnberger's Die Kunst des reinen Satzes in 1774. Soon after, Abbé Georg Joseph Vogler occasionally employed Roman numerals in his Grunde der Kuhrpfälzischen Tonschule in 1778. He mentioned them also in his Handbuch zur Harmonielehre of 1802 and employed Roman numeral analysis in several publications from 1806 onwards.
Gottfried Weber's Versuch einer geordneten Theorie der Tonsetzkunst (Theory of Musical Composition) (1817–21) is often credited with popularizing the method. More precisely, he introduced the usage of large capital numerals for major chords, small capitals for minor, superscript for diminished 5ths and dashed 7 for major sevenths – see the figure hereby. Simon Sechter, considered the founder of the Viennese "Theory of the degrees" (Stufentheorie), made only a limited use of Roman numerals, always as capital letters, and often marked the fundamentals with letter notation or with Arabic numbers. Anton Bruckner, who transmitted the theory to Schoenberg and Schenker, apparently did not use Roman numerals in his classes in Vienna.
The first authors to have made a systematic usage of Roman numerals appear to have been Heinrich Schenker and Arnold Schoenberg, both in their treatise of harmony.
Common practice numerals
See also: Figured bassIn music theory related to or derived from the common practice period, Roman numerals are frequently used to designate scale degrees as well as the chords built on them. In some contexts, however, Arabic numerals with carets are used to designate the scale degrees themselves (e.g. ![]() ,
, ![]() ,
, ![]() , ...).
, ...).
The basic Roman numeral analysis symbols commonly used in pedagogical texts are shown in the table below.
Symbol Meaning Examples Uppercase Roman numeral Major triad I Lowercase Roman numeral Minor triad i Superscript Augmented triad I Superscript Diminished triad i Superscript number Added note V Two or more numbers() Figured bass notation V Superscript and
#First inversion I Second inversion I
4
The Roman numerals for the seven root-position diatonic triads built on the notes of the C major scale are shown below.
In addition, according to Music: In Theory and Practice, "ometimes it is necessary to indicate sharps, flats, or naturals above the bass note." The accidentals may be below the superscript and subscript number(s), before the superscript and subscript number(s), or using a slash (/) or plus sign (+) to indicate that the interval is raised (either ♮ in a flat key signature or a ♯ or ![]() in a sharp key signature.
in a sharp key signature.
Secondary chords are indicated with a slash e.g. V/V.
Modern Schenkerians often prefer the usage of large capital numbers for all degrees in all modes, in conformity with Schenker's own usage.

Inversions

Roman numerals are sometimes complemented by Arabic numerals to denote inversion of the chords. The system is similar to that of Figured bass, the Arabic numerals describing the characteristic interval(s) above the bass note of the chord, the figures 3 and 5 usually being omitted. The first inversion is denoted by the numeral 6 (e.g. I for the first inversion of the tonic triad, even though a complete figuring would require I
3); the numerals
4 denotes the second inversion (e.g. I
4). Inverted seventh chords are similarly denoted by one or two Arabic numerals describing the most characteristic intervals, namely the interval of a second between the 7th and the root: V is the dominant 7th (e.g. G–B–D–F); V
5 is its first inversion (B–D–F–G); V
3 its second inversion (D–F–G–B); and V
2 or V its third inversion (F–G–B–D).
In the United Kingdom, there exists another system where the Roman numerals are paired with Latin letters to denote inversion. In this system, an “a” suffix is used to represent root position, “b” for first inversion, and “c” for second inversion. However, the "a" is rarely used to denote root position, just as
3 is rarely used to denote root position in American nomenclature.
Jazz and pop numerals
Main article: Universal key
In music theory, fake books and lead sheets aimed towards jazz and popular music, many tunes and songs are written in a key, and as such for all chords, a letter name and symbols are given for all triads (e.g., C, G, Dm, etc.). In some fake books and lead sheets, all triads may be represented by upper case numerals, followed by a symbol to indicate if it is not a major chord (e.g. "m" for minor or "" for half-diminished or "7" for a seventh chord). An upper case numeral that is not followed by a symbol is understood as a major chord. The use of Roman numerals enables the rhythm section performers to play the song in any key requested by the bandleader or lead singer. The accompaniment performers translate the Roman numerals to the specific chords that would be used in a given key.
In the key of E major, the diatonic chords are:
- E becomes I (also I, or simply I)
- F♯m becomes II (also II, II, IIm, or II)
- G♯m becomes III (also III, III, IIIm, or III)
- A becomes IV (also IV, or simply IV)
- B becomes V (or simply V; often V or V in a jazz context)
- C♯m becomes VI (also VI, VI, VIm, or VI)
- D♯ becomes VII (also VII, VII, or VII)
In popular music and rock music, "borrowing" of chords from the parallel minor of a major key is commonly done. As such, in these genres, in the key of E major, chords such as D major (or ♭VII), G major (♭III) and C major (♭VI) are commonly used. These chords are all borrowed from the key of E minor. Similarly, in minor keys, chords from the parallel major may also be "borrowed". For example, in E minor, the diatonic chord built on the fourth scale degree is IVm, or A minor. However, in practice, many songs in E minor will use IV (A major), which is borrowed from the key of E major. Borrowing from the parallel major in a minor key, however, is much less common.
Using the V7 or V chord (V dominant 7, or V major) is typical of most jazz and pop music regardless of whether the key is major or minor. Though the V chord is not diatonic to a minor scale, using it in a minor key is not usually considered "borrowing," given its prevalence in these styles.
Diatonic scales
Major scale
The table below shows the Roman numerals for chords built on the major scale.
Scale degree Tonic Supertonic Mediant Subdominant Dominant Submediant Leading tone Conventional notation I ii iii IV V vi vii Alternative notation I II III IV V VI VII Chord symbol I Maj II min III min IV Maj V Maj (or V) VI min VII dim (or VII)
In the key of C major, these chords are
Minor scale
The table below shows the Roman numerals for the chords built on the natural minor scale.
Scale degree Tonic Supertonic Mediant Subdominant Dominant Submediant Subtonic Leading tone Conventional notation i ii ♭III iv v ♭VI ♭VII vii Alternative notation i ii iii iv v vi vii Chord symbol I min II dim ♭III Aug
(or III Maj)IV min
(or IV Maj)V min
(or V)♭VI Maj ♭VII Maj VII dim
(or VII)
In the key of C minor (natural minor), these chords are
The seventh scale degree is very often raised a half step to form a leading tone, making the dominant chord (V) a major chord (i.e. V major instead of v minor) and the subtonic chord (vii), a diminished chord (vii, instead of ♭VII). This version of minor scale is called the harmonic minor scale. This enables composers to have a dominant chord (V) and also the dominant seventh chord (V7) both available for a stronger cadence resolution in the minor key, thus V to i minor.
Modes
In traditional notation, the triads of the seven modern modes are the following:
No. Mode Tonic Supertonic Mediant Subdominant Dominant Submediant Subtonic /
Leading tone1 Ionian (major) I ii iii IV V vi vii 2 Dorian i ii ♭III IV v vi ♭VII 3 Phrygian i ♭II ♭III iv v ♭VI ♭vii 4 Lydian I II iii ♯iv V vi vii 5 Mixolydian I ii iii IV v vi ♭VII 6 Aeolian (natural minor) i ii ♭III iv v ♭VI ♭VII 7 Locrian i ♭II ♭iii iv ♭V ♭VI ♭vii
Footnotes
- As the symbol for a Stufe, the Roman numeral "I" in C major can signify a major chord, a minor chord, a seventh chord, or indeed many combinations of notes controlled by the root C. The same Roman numeral can also represent the governing harmonic function of an extended passage embracing several or many chords. In this system, therefore, one basic sign applies to all manifestations of a structural harmony, with figured-bass numerals and other symbols indicating inversions and deviations from the basic type. ... Roman numerals can be used less to indicate local detail and more broadly, and analytically, to denote harmonic function in either the major or the minor mode. This method assumes fluent knowledge of chord quality in both modes, a skill we consider as fundamental as the recognition of key signatures.
References
- William G Andrews and Molly Sclater (2000). Materials of Western Music Part 1, p. 227. ISBN 1-55122-034-2.
- ^ Roger Sessions (1951). Harmonic Practice. New York: Harcourt, Brace. LCCN 51-8476. p. 7.
- Johann Philipp Kirnberger, Die Kunst des reinen Satzes, vol. I. Berlin und Königsberg, Decker und Hartung, 1774, p. 15 and plates to p. 19. It is not entirely clear, however, whether Roman numerals in Kirnberger denote scale degrees or intervals (or both).
- David Damschroder, Thinking about Harmony: Historical Perspectives on Analysis. ISBN 978-0-521-88814-1. Cambridge University Press, 2008, p. 6
- Floyd K. Grave and Margaret G. Grave, In Praise of Harmony: The Teachings of Abbé Georg Joseph Vogler, Lincoln and London, University of Nebraska Press,1987, among others pp. 70-71, 169-170, and passim.
- Gottfried Weber, Versuch einer geordneten Theorie der Tonsetzkunst, 3d Edition, Mainz, Schott, 1830–1832, vol. 2, pp. 44–63, §§ 151–158.
- Simon Sechter, Die Richtige Folge der Grundharmonien, Leipzig, Breitkopf und Härtel, 3 vols., 1853–1854. Roman numerals are found in all three volumes.
- Anton Bruckner, Vorlesungen über Harmonielehre und Kontrapunkt an der Universität Wien, E. Schwanzara ed., Wien, Östrereichischer Bundesverlag, 1950. See also Robert E. Wason, Viennese Harmonic Theory from Albrechtsberger to Schenker and Schoenberg, Ann Arbor, UMI Research Press, 1982. ISBN 0-8357-1586-8. pp. 67–84.
- Heinrich Schenker, Harmonielehre, Stuttgart, Berlin, Cotta, 1906; Arnold Schoenberg, Harmonielehre, Vienna, Universal, 1911.
- Eric Taylor (1989). The AB Guide to Music Theory. Vol. Part 1. London: Associated Board of the Royal Schools of Music. pp. 60–61. ISBN 1-85472-446-0.
- ^ Bruce Benward; Marilyn Nadine Saker (2003). Music: In Theory and Practice. Vol. I (seventh ed.). Boston: McGraw-Hill. ISBN 978-0-07-294262-0.
- Edward Aldwell; Carl Schachter; Allen Cadwallader (2011). Harmony and Voice Leading (4th ed.). Schirmer, Cengage Learning. pp. 696–697. ISBN 978-0-495-18975-6.
- Heinrich Schenker, Harmonielehre, Stuttgart, Berlin, Cotta, 1906, p. 186, Example 151.
- Lovelock, William (1981). The Rudiments of Music. London: Bell & Hyman. ISBN 0-7135-0744-6.
- "musictheory.net". www.musictheory.net. Retrieved 2020-11-29.
- Ben (2013-12-02). "Chord Inversions". Music Theory Academy. Retrieved 2020-12-06.
- Robson, Elsie May (1960s). Harmony, Melodic Invention, Instruments of the Orchestra, Form in Music. Sydney: Nicholson's.
- Spearritt, Gordon (1995). Essential Music Theory. Melbourne: Allans Educational.
- John Mehegan (1989). Tonal and Rhythmic Principles. Jazz Improvisation. Vol. 1 (Revised and Enlarged ed.). New York: Watson-Guptill. pp. 9–16. ISBN 0-8230-2559-4.
| Chord progressions | |||||
|---|---|---|---|---|---|
| Terminology | |||||
| By number of chords |
| ||||
| By name | |||||
| Related | |||||
| List of chord progressions | |||||
| Chord symbols | |
|---|---|
| Musical analysis | |
|---|---|