Misplaced Pages

Siacci's theorem

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.

In kinematics, the acceleration of a particle moving along a curve in space is the time derivative of its velocity. In most applications, the acceleration vector is expressed as the sum of its normal and tangential components, which are orthogonal to each other. Siacci's theorem, formulated by the Italian mathematician Francesco Siacci (1839–1907), is the kinematical decomposition of the acceleration vector into its radial and tangential components. In general, the radial and tangential components are not orthogonal to each other. Siacci's theorem is particularly useful in motions where the angular momentum is constant.

Siacci's theorem in the plane

Motion of a particle P in a plane.

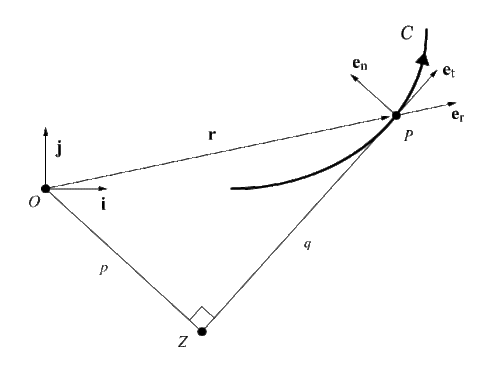
Let a particle P of mass m  move in a two-dimensional Euclidean space (planar motion). Suppose that C is the curve traced out by P and s is the arc length of C corresponding to time t. Let O be an arbitrary origin in the plane and {i,j} be a fixed orthonormal basis. The position vector of the particle is

r = r e r . {\displaystyle \mathbf {r} =r\mathbf {e} _{r}.}

The unit vector er is the radial basis vector of a polar coordinate system in the plane. The velocity vector of the particle is

v = d r d t = s ˙ e t = v e t , {\displaystyle \mathbf {v} ={\frac {d\mathbf {r} }{dt}}={\dot {s}}\mathbf {e} _{t}=v\mathbf {e} _{t},}

where et is the unit tangent vector to C. Define the angular momentum of P as

h = r × m v = h k , {\displaystyle \mathbf {h} =\mathbf {r} \times m\mathbf {v} =h\mathbf {k} ,}

where k = i x j. Assume that h ≠ 0. The position vector r may then be expressed as

r = q e t − p e n {\displaystyle \mathbf {r} =q\mathbf {e} _{t}-p\mathbf {e} _{n}}

in the Serret-Frenet Basis {et, en, eb}. The magnitude of the angular momentum is h = mpv, where p is the perpendicular from the origin to the tangent line ZP. According to Siacci's theorem, the acceleration a of P can be expressed as

a = − κ v 2 r p e r + ( h 2 ) ′ 2 p 2 e t = S r e r + S t e t . {\displaystyle \mathbf {a} =-{\frac {\kappa v^{2}r}{p}}\mathbf {e} _{r}+{\frac {(h^{2})'}{2p^{2}}}\mathbf {e} _{t}=S_{r}\mathbf {e} _{r}+S_{t}\mathbf {e} _{t}.}

where the prime denotes differentiation with respect to the arc length s, and κ is the curvature function of the curve C. In general, Sr and St are not equal to the orthogonal projections of a onto er and et.

Example: Central forces

Suppose that the angular momentum of the particle P is a nonzero constant and that Sr is a function of r. Then

S r = − f ( r ) = − κ r h 2 p 3 , S t = 0. {\displaystyle S_{r}=-f(r)=-{\frac {\kappa rh^{2}}{p^{3}}},\qquad S_{t}=0.}

Because the curvature at a point in an orbit is given by

κ = 1 r d p d r , {\displaystyle \kappa ={\frac {1}{r}}{\frac {dp}{dr}},}

the function f can be conveniently written as a first order ODE

f ( r ) = h 2 p 3 d p d r . {\displaystyle f(r)={\frac {h^{2}}{p^{3}}}{\frac {dp}{dr}}.}

The energy conservation equation for the particle is then obtained if f(r) is integrable.

1 2 h 2 p 2 + ∫ f ( r ) = c o n s t a n t . {\displaystyle {\frac {1}{2}}{\frac {h^{2}}{p^{2}}}+\int f(r)=\mathrm {constant} .}

Siacci's theorem in space

Siacci's theorem can be extended to three-dimensional motions. Thus, let C be a space curve traced out by P and s is the arc length of C corresponding to time t. Also, suppose that the binormal component of the angular momentum does not vanish. Then the acceleration vector of P can be expressed as

a = − κ v 2 r p e r + ( v d v d s + κ v 2 q p ) e t . {\displaystyle \mathbf {a} =-{\frac {\kappa v^{2}r}{p}}\mathbf {e} _{r}+\left(v{\frac {dv}{ds}}+{\frac {\kappa v^{2}q}{p}}\right)\mathbf {e} _{t}.}

The tangential component is tangent to the curve C. The radial component is directed from the point P to the point where the perpendicular from an arbitrary fixed origin meets the osculating plane. Other expressions for a can be found in, where a new proof of Siacci's theorem is given.

See also

References

  1. Casey, James (2011). "Siacci's resolution of the acceleration vector for a space curve". Meccanica. 46 (2): 471–476. doi:10.1007/s11012-010-9296-x.
  • F. Siacci. Moto per una linea plana. Atti della Reale Accademia della Scienze di Torino, XIV, 750–760, 1879.
  • F. Siacci. Moto per una linea gobba. Atti della Reale Accademia della Scienze di Torino, XIV, 946–951, 1879.
  • E. T. Whittaker. A Treatise on the Analytical Dynamics of Particles and Rigid Bodies. 4th edition, Cambridge University Press, Cambridge. Reprinted by Dover Publications, Inc., New York (1944).
  • Nathaniel Grossman. The sheer joy of celestial mechanics. Birkhäuser, Basel, 1996.
Categories: