Misplaced Pages

Silicon bandgap temperature sensor

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.

The silicon bandgap temperature sensor is an extremely common form of temperature sensor (thermometer) used in electronic equipment. Its main advantage is that it can be included in a silicon integrated circuit at very low cost. The principle of the sensor is that the forward voltage of a silicon diode, which may be the base-emitter junction of a bipolar junction transistor (BJT), is temperature-dependent, according to the following equation:

V B E = V G 0 ( 1 − T T 0 ) + V B E 0 ( T T 0 ) + ( n k T q ) ln ⁡ ( T 0 T ) + ( k T q ) ln ⁡ ( I C I C 0 ) {\displaystyle V_{BE}=V_{G0}\left(1-{\frac {T}{T_{0}}}\right)+V_{BE0}\left({\frac {T}{T_{0}}}\right)+\left({\frac {nkT}{q}}\right)\ln \left({\frac {T_{0}}{T}}\right)+\left({\frac {kT}{q}}\right)\ln \left({\frac {I_{C}}{I_{C0}}}\right)\,}

where

T = temperature in kelvins,
T0 = reference temperature,
VG0 = bandgap voltage at absolute zero,
VBE0 = junction voltage at temperature T0 and current IC0,
k = Boltzmann constant,
q = charge on an electron,
n = a device-dependent constant.
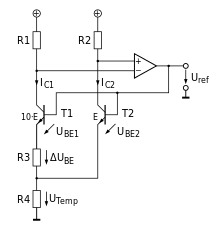
Circuit of a Brokaw bandgap reference

By comparing the voltages of two junctions at the same temperature, but at two different currents, IC1 and IC2, many of the variables in the above equation can be eliminated, resulting in the relationship:

Δ V B E = k T q ⋅ ln ⁡ ( I C 1 I C 2 ) {\displaystyle \Delta V_{BE}={\frac {kT}{q}}\cdot \ln \left({\frac {I_{C1}}{I_{C2}}}\right)\,}

Note that the junction voltage is a function of current density, i.e. current/junction area, and a similar output voltage can be obtained by operating the two junctions at the same current, if one is of a different area to the other.

A circuit that forces IC1 and IC2 to have a fixed N:1 ratio, gives the relationship:

Δ V B E = k T q ⋅ ln ⁡ ( N ) {\displaystyle \Delta V_{BE}={\frac {kT}{q}}\cdot \ln \left(N\right)\,}

An electronic circuit, such as the Brokaw bandgap reference, that measures ΔVBE can therefore be used to calculate the temperature of the diode. The result remains valid up to about 200 °C to 250 °C, when leakage currents become large enough to corrupt the measurement. Above these temperatures, materials such as silicon carbide can be used instead of silicon.

The voltage difference between two p-n junctions (e.g. diodes), operated at different current densities, is proportional to absolute temperature (PTAT).

PTAT circuits using either BJT or CMOS transistors are widely used in temperature sensors (where we want the output to vary with temperature), and also in bandgap voltage references and other temperature-compensating circuits (where we want the same output at every temperature).

If high precision is not required it is enough to bias a diode with any constant low current and use its −2 mV/˚C thermal coefficient for temperature calculation, however this requires calibration for each diode type. This method is common in monolithic temperature sensors.

References

  1. Widlar, R.J. (January 1967). "An exact expression for the thermal variation of the emitter base voltage of bi-polar transistors". Proceedings of the IEEE. 55 (1): 96–97. doi:10.1109/PROC.1967.5396. ISSN 0018-9219.
  2. ^ James Bryant. "IC Temperature Sensors" Archived 2013-08-27 at archive.today. Analog Devices. 2008.
  3. C. Rossi, C. Galup-Montoro, and M. C. Schneider. "PTAT Voltage Generator based on an MOS Voltage Divider". Nanotechnology Conference and Trade Show, Technical Proceedings, 2007.
  4. Andre Luiz Aita and Cesar Ramos Rodrigues. "PTAT CMOS Current Sources Mismatch over Temperature". The 26th Symposium on Integrated Circuits and System Design (SBCCI 2013). 2013.

External links

Category: