| This article's lead section contains information that is not included elsewhere in the article. If the information is appropriate for the lead of the article, this information should also be included in the body of the article. (May 2020) (Learn how and when to remove this message) |
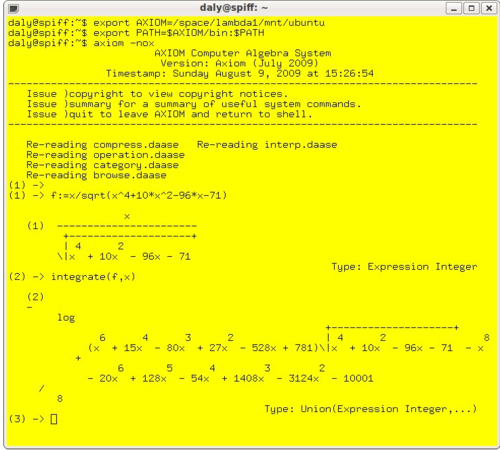
In mathematics and computer science, computer algebra, also called symbolic computation or algebraic computation, is a scientific area that refers to the study and development of algorithms and software for manipulating mathematical expressions and other mathematical objects. Although computer algebra could be considered a subfield of scientific computing, they are generally considered as distinct fields because scientific computing is usually based on numerical computation with approximate floating point numbers, while symbolic computation emphasizes exact computation with expressions containing variables that have no given value and are manipulated as symbols.
Software applications that perform symbolic calculations are called computer algebra systems, with the term system alluding to the complexity of the main applications that include, at least, a method to represent mathematical data in a computer, a user programming language (usually different from the language used for the implementation), a dedicated memory manager, a user interface for the input/output of mathematical expressions, a large set of routines to perform usual operations, like simplification of expressions, differentiation using the chain rule, polynomial factorization, indefinite integration, etc.
Computer algebra is widely used to experiment in mathematics and to design the formulas that are used in numerical programs. It is also used for complete scientific computations, when purely numerical methods fail, as in public key cryptography, or for some non-linear problems.
Terminology
Some authors distinguish computer algebra from symbolic computation using the latter name to refer to kinds of symbolic computation other than the computation with mathematical formulas. Some authors use symbolic computation for the computer science aspect of the subject and "computer algebra" for the mathematical aspect. In some languages the name of the field is not a direct translation of its English name. Typically, it is called calcul formel in French, which means "formal computation". This name reflects the ties this field has with formal methods.
Symbolic computation has also been referred to, in the past, as symbolic manipulation, algebraic manipulation, symbolic processing, symbolic mathematics, or symbolic algebra, but these terms, which also refer to non-computational manipulation, are no longer used in reference to computer algebra.
Scientific community
There is no learned society that is specific to computer algebra, but this function is assumed by the special interest group of the Association for Computing Machinery named SIGSAM (Special Interest Group on Symbolic and Algebraic Manipulation).
There are several annual conferences on computer algebra, the premier being ISSAC (International Symposium on Symbolic and Algebraic Computation), which is regularly sponsored by SIGSAM.
There are several journals specializing in computer algebra, the top one being Journal of Symbolic Computation founded in 1985 by Bruno Buchberger. There are also several other journals that regularly publish articles in computer algebra.
Computer science aspects
Data representation
As numerical software is highly efficient for approximate numerical computation, it is common, in computer algebra, to emphasize exact computation with exactly represented data. Such an exact representation implies that, even when the size of the output is small, the intermediate data generated during a computation may grow in an unpredictable way. This behavior is called expression swell. To obviate this problem, various methods are used in the representation of the data, as well as in the algorithms that manipulate them.
Numbers
The usual numbers systems used in numerical computation are floating point numbers and integers of a fixed bounded size. Neither of these is convenient for computer algebra, due to expression swell.
Therefore, the basic numbers used in computer algebra are the integers of the mathematicians, commonly represented by an unbounded signed sequence of digits in some base of numeration, usually the largest base allowed by the machine word. These integers allow to define the rational numbers, which are irreducible fractions of two integers.
Programming an efficient implementation of the arithmetic operations is a hard task. Therefore, most free computer algebra systems and some commercial ones such as Mathematica and Maple, use the GMP library, which is thus a de facto standard.
Expressions
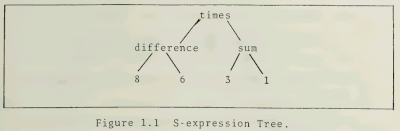
Except for numbers and variables, every mathematical expression may be viewed as the symbol of an operator followed by a sequence of operands. In computer algebra software, the expressions are usually represented in this way. This representation is very flexible, and many things that seem not to be mathematical expressions at first glance, may be represented and manipulated as such. For example, an equation is an expression with "=" as an operator, a matrix may be represented as an expression with "matrix" as an operator and its rows as operands.
Even programs may be considered and represented as expressions with operator "procedure" and, at least, two operands, the list of parameters and the body, which is itself an expression with "body" as an operator and a sequence of instructions as operands. Conversely, any mathematical expression may be viewed as a program. For example, the expression a + b may be viewed as a program for the addition, with a and b as parameters. Executing this program consists in evaluating the expression for given values of a and b; if they are not given any values, the result of the evaluation is simply its input.
This process of delayed evaluation is fundamental in computer algebra. For example, the operator "=" of the equations is also, in most computer algebra systems, the name of the program of the equality test: normally, the evaluation of an equation results in an equation, but, when an equality test is needed, either explicitly asked by the user through an "evaluation to a Boolean" command, or automatically started by the system in the case of a test inside a program, then the evaluation to a Boolean result is executed.
As the size of the operands of an expression is unpredictable and may change during a working session, the sequence of the operands is usually represented as a sequence of either pointers (like in Macsyma) or entries in a hash table (like in Maple).
Simplification
The raw application of the basic rules of differentiation with respect to x on the expression gives the result
A simpler expression than this is generally desired, and simplification is needed when working with general expressions.
This simplification is normally done through rewriting rules. There are several classes of rewriting rules to be considered. The simplest are rules that always reduce the size of the expression, like E − E → 0 or sin(0) → 0. They are systematically applied in computer algebra systems.
A difficulty occurs with associative operations like addition and multiplication. The standard way to deal with associativity is to consider that addition and multiplication have an arbitrary number of operands, that is that a + b + c is represented as "+"(a, b, c). Thus a + (b + c) and (a + b) + c are both simplified to "+"(a, b, c), which is displayed a + b + c. In the case of expressions such as a − b + c, the simplest way is to systematically rewrite −E, E − F, E/F as, respectively, (−1)⋅E, E + (−1)⋅F, E⋅F. In other words, in the internal representation of the expressions, there is no subtraction nor division nor unary minus, outside the representation of the numbers.
Another difficulty occurs with the commutativity of addition and multiplication. The problem is to quickly recognize the like terms in order to combine or cancel them. Testing every pair of terms is costly with very long sums and products. To address this, Macsyma sorts the operands of sums and products into an order that places like terms in consecutive places, allowing easy detection. In Maple, a hash function is designed for generating collisions when like terms are entered, allowing them to be combined as soon as they are introduced. This allows subexpressions that appear several times in a computation to be immediately recognized and stored only once. This saves memory and speeds up computation by avoiding repetition of the same operations on identical expressions.
Some rewriting rules sometimes increase and sometimes decrease the size of the expressions to which they are applied. This is the case of distributivity or trigonometric identities. For example, the distributivity law allows rewriting and As there is no way to make a good general choice of applying or not such a rewriting rule, such rewriting is done only when explicitly invoked by the user. For the distributivity, the computer function that applies this rewriting rule is typically called "expand". The reverse rewriting rule, called "factor", requires a non-trivial algorithm, which is thus a key function in computer algebra systems (see Polynomial factorization).
Mathematical aspects
Some fundamental mathematical questions arise when one wants to manipulate mathematical expressions in a computer. We consider mainly the case of the multivariate rational fractions. This is not a real restriction, because, as soon as the irrational functions appearing in an expression are simplified, they are usually considered as new indeterminates. For example,
is viewed as a polynomial in and
Equality
There are two notions of equality for mathematical expressions. Syntactic equality is the equality of their representation in a computer. This is easy to test in a program. Semantic equality is when two expressions represent the same mathematical object, as in
It is known from Richardson's theorem that there may not exist an algorithm that decides whether two expressions representing numbers are semantically equal if exponentials and logarithms are allowed in the expressions. Accordingly, (semantic) equality may be tested only on some classes of expressions such as the polynomials and rational fractions.
To test the equality of two expressions, instead of designing specific algorithms, it is usual to put expressions in some canonical form or to put their difference in a normal form, and to test the syntactic equality of the result.
In computer algebra, "canonical form" and "normal form" are not synonymous. A canonical form is such that two expressions in canonical form are semantically equal if and only if they are syntactically equal, while a normal form is such that an expression in normal form is semantically zero only if it is syntactically zero. In other words, zero has a unique representation as an expression in normal form.
Normal forms are usually preferred in computer algebra for several reasons. Firstly, canonical forms may be more costly to compute than normal forms. For example, to put a polynomial in canonical form, one has to expand every product through distributivity, while it is not necessary with a normal form (see below). Secondly, it may be the case, like for expressions involving radicals, that a canonical form, if it exists, depends on some arbitrary choices and that these choices may be different for two expressions that have been computed independently. This may make impracticable the use of a canonical form.
History
Human-driven computer algebra
Early computer algebra systems, such as the ENIAC at the University of Pennsylvania, relied on human computers or programmers to reprogram it between calculations, manipulate its many physical modules (or panels), and feed its IBM card reader. Female mathematicians handled the majority of ENIAC programming human-guided computation: Jean Jennings, Marlyn Wescoff, Ruth Lichterman, Betty Snyder, Frances Bilas, and Kay McNulty led said efforts.
Foundations and early applications
In 1960, John McCarthy explored an extension of primitive recursive functions for computing symbolic expressions through the Lisp programming language while at the Massachusetts Institute of Technology. Though his series on "Recursive functions of symbolic expressions and their computation by machine" remained incomplete, McCarthy and his contributions to artificial intelligence programming and computer algebra via Lisp helped establish Project MAC at the Massachusetts Institute of Technology and the organization that later became the Stanford AI Laboratory (SAIL) at Stanford University, whose competition facilitated significant development in computer algebra throughout the late 20th century.
Early efforts at symbolic computation, in the 1960s and 1970s, faced challenges surrounding the inefficiency of long-known algorithms when ported to computer algebra systems. Predecessors to Project MAC, such as ALTRAN, sought to overcome algorithmic limitations through advancements in hardware and interpreters, while later efforts turned towards software optimization.
Historic problems
A large part of the work of researchers in the field consisted of revisiting classical algebra to increase its effectiveness while developing efficient algorithms for use in computer algebra. An example of this type of work is the computation of polynomial greatest common divisors, a task required to simplify fractions and an essential component of computer algebra. Classical algorithms for this computation, such as Euclid's algorithm, proved inefficient over infinite fields; algorithms from linear algebra faced similar struggles. Thus, researchers turned to discovering methods of reducing polynomials (such as those over a ring of integers or a unique factorization domain) to a variant efficiently computable via a Euclidean algorithm.
Algorithms used in computer algebra
This section is an excerpt from List of algorithms § Computer algebra.- Buchberger's algorithm: finds a Gröbner basis
- Cantor–Zassenhaus algorithm: factor polynomials over finite fields
- Faugère F4 algorithm: finds a Gröbner basis (also mentions the F5 algorithm)
- Gosper's algorithm: find sums of hypergeometric terms that are themselves hypergeometric terms
- Knuth–Bendix completion algorithm: for rewriting rule systems
- Multivariate division algorithm: for polynomials in several indeterminates
- Pollard's kangaroo algorithm (also known as Pollard's lambda algorithm ): an algorithm for solving the discrete logarithm problem
- Polynomial long division: an algorithm for dividing a polynomial by another polynomial of the same or lower degree
- Risch algorithm: an algorithm for the calculus operation of indefinite integration (i.e. finding antiderivatives)
See also
- Automated theorem prover
- Computer-assisted proof
- Computational algebraic geometry
- Computer algebra system
- Differential analyser
- Proof checker
- Model checker
- Symbolic-numeric computation
- Symbolic simulation
- Symbolic artificial intelligence
References
- "ACM Association in computer algebra".
- Watt, Stephen M. (2006). Making Computer Algebra More Symbolic (Invited) (PDF). Transgressive Computing 2006: A conference in honor of Jean Della Dora, (TC 2006). pp. 43–49. ISBN 9788468983813. OCLC 496720771.
- SIGSAM official site
- "SIGSAM list of conferences". Archived from the original on 2013-08-08. Retrieved 2012-11-15.
- Cohen, Joel S. (2003). Computer Algebra and Symbolic Computation: Mathematical Methods. AK Peters. p. 14. ISBN 978-1-56881-159-8.
- SIGSAM list of journals
- "Lecture 12: Rational Functions and Conversions — Introduction to Symbolic Computation 1.7.6 documentation". homepages.math.uic.edu. Retrieved 2024-03-31.
- Neut, Sylvain; Petitot, Michel; Dridi, Raouf (2009-03-01). "Élie Cartan's geometrical vision or how to avoid expression swell". Journal of Symbolic Computation. Polynomial System Solving in honor of Daniel Lazard. 44 (3): 261–270. doi:10.1016/j.jsc.2007.04.006. ISSN 0747-7171.
- Richard Liska Expression swell, from "Peculiarities of programming in computer algebra systems"
- "The Mathematica Kernel: Issues in the Design and Implementation". October 2006. Retrieved 2023-11-29.
- "The GNU Multiple Precision (GMP) Library". Maplesoft. Retrieved 2023-11-29.
- Cassidy, Kevin G. (Dec 1985). The Feasibility of Automatic Storage Reclamation with Concurrent Program Execution in a LISP Environment (PDF) (Master's thesis). Naval Postgraduate School, Monterey/CA. p. 15. ADA165184.
- Macsyma Mathematics and System Reference Manual (PDF). Macsyma. 1996. p. 419.
- Buchberger, Bruno; Loos, Rüdiger (1983). "Algebraic simplification" (PDF). In Buchberger, Bruno; Collins, George Edwin; Loos, Rüdiger; Albrecht, Rudolf (eds.). Computer Algebra: Symbolic and Algebraic Computation. Computing Supplementa. Vol. 4. pp. 11–43. doi:10.1007/978-3-7091-7551-4_2. ISBN 978-3-211-81776-6.
- Davenport, J. H.; Siret, Y.; Tournier, É. (1988). Computer Algebra: Systems and Algorithms for Algebraic Computation. Academic. ISBN 0-12-204230-1. OCLC 802584470.
- "ENIAC in Action: What it Was and How it Worked". ENIAC: Celebrating Penn Engineering History. University of Pennsylvania. Retrieved December 3, 2023.
- Light, Jennifer S. (1999). "When Computers Were Women". Technology and Culture. 40 (3): 455–483. doi:10.1353/tech.1999.0128. ISSN 1097-3729.
- McCarthy, John (1960-04-01). "Recursive functions of symbolic expressions and their computation by machine, Part I". Communications of the ACM. 3 (4): 184–195. doi:10.1145/367177.367199. ISSN 0001-0782.
- Wexelblat, Richard L. (1981). History of programming languages. ACM monograph series. History of programming languages conference, Association for computing machinery. New York London Toronto: Academic press. ISBN 978-0-12-745040-7.
- "Symbolic Computation (An Editorial)". Journal of Symbolic Computation. 1 (1): 1–6. 1985-03-01. doi:10.1016/S0747-7171(85)80025-0. ISSN 0747-7171.
- Feldman, Stuart I. (1975-11-01). "A brief description of Altran". ACM SIGSAM Bulletin. 9 (4): 12–20. doi:10.1145/1088322.1088325. ISSN 0163-5824.
- Kaltofen, E. (1983), Buchberger, Bruno; Collins, George Edwin; Loos, Rüdiger; Albrecht, Rudolf (eds.), "Factorization of Polynomials", Computer Algebra, Computing Supplementa, vol. 4, Vienna: Springer Vienna, pp. 95–113, doi:10.1007/978-3-7091-7551-4_8, ISBN 978-3-211-81776-6, retrieved 2023-11-29
Further reading
For a detailed definition of the subject:
- Buchberger, Bruno (1985). "Symbolic Computation (An Editorial)" (PDF). Journal of Symbolic Computation. 1 (1): 1–6. doi:10.1016/S0747-7171(85)80025-0.
For textbooks devoted to the subject:
- Davenport, James H.; Siret, Yvon; Tournier, Èvelyne (1988). Computer Algebra: Systems and Algorithms for Algebraic Computation. Translated from the French by A. Davenport and J. H. Davenport. Academic Press. ISBN 978-0-12-204230-0.
- von zur Gathen, Joachim; Gerhard, Jürgen (2003). Modern computer algebra (2nd ed.). Cambridge University Press. ISBN 0-521-82646-2.
- Geddes, K. O.; Czapor, S. R.; Labahn, G. (1992). Algorithms for Computer Algebra. Bibcode:1992afca.book.....G. doi:10.1007/b102438. ISBN 978-0-7923-9259-0.
- Buchberger, Bruno; Collins, George Edwin; Loos, Rüdiger; Albrecht, Rudolf, eds. (1983). Computer Algebra: Symbolic and Algebraic Computation. Computing Supplementa. Vol. 4. doi:10.1007/978-3-7091-7551-4. ISBN 978-3-211-81776-6. S2CID 5221892.
| Computer algebra systems | |
|---|---|
| Open-source | |
| Proprietary |
|
| Discontinued | |
| Major mathematics areas | |
|---|---|
| Foundations | |
| Algebra | |
| Analysis | |
| Discrete | |
| Geometry | |
| Number theory | |
| Topology | |
| Applied | |
| Computational | |
| Related topics | |
 gives the result
gives the result

 and
and  As there is no way to make a good general choice of applying or not such a rewriting rule, such rewriting is done only when explicitly invoked by the user. For the distributivity, the computer function that applies this rewriting rule is typically called "expand". The reverse rewriting rule, called "factor", requires a non-trivial algorithm, which is thus a key function in computer algebra systems (see
As there is no way to make a good general choice of applying or not such a rewriting rule, such rewriting is done only when explicitly invoked by the user. For the distributivity, the computer function that applies this rewriting rule is typically called "expand". The reverse rewriting rule, called "factor", requires a non-trivial algorithm, which is thus a key function in computer algebra systems (see 
 and
and 
