Computational hardness assumption
The small set expansion hypothesis or small set expansion conjecture in computational complexity theory is an unproven computational hardness assumption. Under the small set expansion hypothesis it is assumed to be computationally infeasible to distinguish between a certain class of expander graphs called "small set expanders" and other graphs that are very far from being small set expanders. This assumption implies the hardness of several other computational problems, and the optimality of certain known approximation algorithms.
The small set expansion hypothesis is related to the unique games conjecture, another unproven computational hardness assumption according to which accurately approximating the value of certain games is computationally infeasible. If the small set expansion hypothesis is true, then so is the unique games conjecture.
Background
The edge expansion of a set of vertices in a graph is defined as where the vertical bars denote the number of elements of a set, and denotes the set of edges that have one endpoint in and the other endpoint in its complement. This number can be as low as zero, when is a connected component of the graph, because in this case there are no edges connecting to other parts of the graph. A graph is called regular or -regular when every vertex is incident to the same number of edges, , the degree of the graph. For a -regular graph, the maximum possible edge expansion is . This expansion is achieved by any subset that induces an independent set, as in this case all of the edges that touch vertices in belong to .
The edge expansion of a graph with vertices is defined to be the minimum edge expansion among its subsets of at most vertices. Instead, the small set expansion is defined as the same minimum, but only over smaller subsets, of at most vertices. Informally, a small set expander is a graph whose small set expansion is large.
Statement
The small set expansion hypothesis uses a real number as a parameter to formalize what it means for the small set expansion of a graph to be large or small. It asserts that, for every , it is NP-hard to distinguish between -regular graphs with small set expansion at least (good small set expanders), and -regular graphs with small set expansion at most (very far from being a small set expander). Here, the degree is a variable that might depend on the choice of , unlike in many applications of expander graphs where the degree is assumed to be a fixed constant.
Consequences
The small set expansion hypothesis implies the NP-hardness of several other computational problems. Because it is only a hypothesis, this does not prove that these problems actually are NP-hard. Nevertheless, it suggests that it would be difficult to find an efficient solution for these problems, because solving any one of them would also solve other problems whose solution has so far been elusive (including the small set expansion problem itself). In the other direction, this implication opens the door to disproving the small set expansion hypothesis, by providing other problems through which it could be attacked.
In particular, there exists a polynomial-time reduction from the recognition of small set expanders to the problem of determining the approximate value of unique games, showing that the small set expansion hypothesis implies the unique games conjecture. Boaz Barak has suggested more strongly that these two hypotheses are equivalent. In fact, the small set expansion hypothesis is equivalent to a restricted form of the unique games conjecture, asserting the hardness of unique games instances whose underlying graphs are small set expanders. On the other hand, it is possible to quickly solve unique games instances whose graph is "certifiably" a small set expander, in the sense that their expansion can be verified by sum-of-squares optimization.
Another application of the small set expansion hypothesis concerns the computational problem of approximating the treewidth of graphs, a structural parameter closely related to expansion. For graphs of treewidth , the best approximation ratio known for a polynomial time approximation algorithm is . The small set expansion hypothesis, if true, implies that there does not exist an approximation algorithm for this problem with constant approximation ratio. It also can be used to imply the inapproximability of finding a complete bipartite graph with the maximum number of edges (possibly restricted to having equal numbers of vertices on each side of its bipartition) in a larger graph.
The small set expansion hypothesis implies the optimality of known approximation ratios for certain variants of the edge cover problem, in which one must choose as few vertices as possible to cover a given number of edges in a graph.
History and partial results
The small set expansion hypothesis was formulated, and connected to the unique games conjecture, by Prasad Raghavendra and David Steurer in 2010, as part of a body of work for which they were given the 2018 Michael and Sheila Held Prize of the National Academy of Sciences.
One approach to resolving the small set expansion hypothesis is to seek approximation algorithms for the edge expansion of small vertex sets that would be good enough to distinguish the two classes of graphs in the hypothesis. In this light, the best approximation known, for the edge expansion of subsets of at most vertices in a -regular graph, has an approximation ratio of . This is not strong enough to refute the hypothesis; doing so would require finding an algorithm with a bounded approximation ratio.
Notes
- This definition follows the notation used in the expander graph article; some sources, such as Raghavendra & Steurer (2010), instead normalize the edge expansion by dividing it by the degree of the graph.
- This definition avoids using subsets whose number of vertices is close to , because these subsets would have small expansion even in graphs that otherwise have high expansion.
- ^ This formulation is from Barak (2016), who notes that it eliminates some unimportant parameters appearing in other formulations of the same hypothesis, such as that in Raghavendra & Steurer (2010).
References
- ^ Barak, Boaz (2016), "SOS Lecture 6: The SOS approach to refuting the UGC" (PDF), Lecture notes on "Proofs, beliefs and algorithms through the lens of Sum of Squares", retrieved 2023-03-14
- ^ Raghavendra, Prasad; Steurer, David (2010), "Graph expansion and the unique games conjecture", in Schulman, Leonard J. (ed.), Proceedings of the 42nd ACM Symposium on Theory of Computing, STOC 2010, Cambridge, Massachusetts, USA, 5–8 June 2010 (PDF), Association for Computing Machinery, pp. 755–764, doi:10.1145/1806689.1806792, S2CID 1601199
- Raghavendra, Prasad; Steurer, David; Tulsiani, Madhur (2012), "Reductions between expansion problems", Proceedings of the 27th Conference on Computational Complexity, CCC 2012, Porto, Portugal, June 26–29, 2012, IEEE Computer Society, pp. 64–73, arXiv:1011.2586, doi:10.1109/CCC.2012.43
- Bafna, Mitali; Barak, Boaz; Kothari, Pravesh K.; Schramm, Tselil; Steurer, David (2021), "Playing unique games on certified small-set expanders", in Khuller, Samir; Williams, Virginia Vassilevska (eds.), STOC '21: 53rd Annual ACM SIGACT Symposium on Theory of Computing, Virtual Event, Italy, June 21–25, 2021, Association for Computing Machinery, pp. 1629–1642, arXiv:2006.09969, doi:10.1145/3406325.3451099
- Feige, Uriel; Hajiaghayi, Mohammadtaghi; Lee, James R. (2008), "Improved approximation algorithms for minimum weight vertex separators", SIAM Journal on Computing, 38 (2): 629–657, doi:10.1137/05064299X, MR 2411037
- Wu, Yu; Austrin, Per; Pitassi, Toniann; Liu, David (2014), "Inapproximability of treewidth, one-shot pebbling, and related layout problems", Journal of Artificial Intelligence Research, 49: 569–600, doi:10.1613/jair.4030, MR 3195329
- Manurangsi, Pasin (2018), "Inapproximability of maximum biclique problems, minimum k-cut and densest at-least-k-subgraph from the small set expansion hypothesis", Algorithms, 11 (1): P10:1–P10:22, arXiv:1705.03581, doi:10.3390/a11010010, MR 3758880
- Gandhi, Rajiv; Kortsarz, Guy (2015), "On set expansion problems and the small set expansion conjecture" (PDF), Discrete Applied Mathematics, 194: 93–101, doi:10.1016/j.dam.2015.05.028, MR 3391764
- 2018 Michael and Sheila Held Prize: Prasad Raghavendra and David Steurer, National Academy of Sciences, retrieved 2023-11-23
- Bansal, Nikhil; Feige, Uriel; Krauthgamer, Robert; Makarychev, Konstantin; Nagarajan, Viswanath; Naor, Joseph; Schwartz, Roy (2014), "Min-max graph partitioning and small set expansion" (PDF), SIAM Journal on Computing, 43 (2): 872–904, doi:10.1137/120873996, MR 3504685
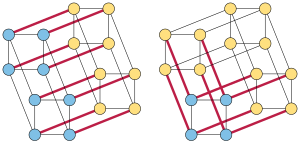
 for the eight red edges and eight blue vertices shown on the left, so its edge expansion is 1. For small sets of at most
for the eight red edges and eight blue vertices shown on the left, so its edge expansion is 1. For small sets of at most  vertices, the minimum edge-to-vertex ratio is
vertices, the minimum edge-to-vertex ratio is  , for the eight red edges and four blue vertices at right, so its small set expansion is 2.
, for the eight red edges and four blue vertices at right, so its small set expansion is 2. of vertices in a graph
of vertices in a graph  is defined as
is defined as  where the vertical bars denote the
where the vertical bars denote the  denotes the set of edges that have one endpoint in
denotes the set of edges that have one endpoint in  -regular when every vertex is incident to the same number of edges,
-regular when every vertex is incident to the same number of edges,  vertices is defined to be the minimum edge expansion among its subsets of at most
vertices is defined to be the minimum edge expansion among its subsets of at most  vertices. Instead, the small set expansion is defined as the same minimum, but only over smaller subsets, of at most
vertices. Instead, the small set expansion is defined as the same minimum, but only over smaller subsets, of at most  vertices. Informally, a small set expander is a graph whose small set expansion is large.
vertices. Informally, a small set expander is a graph whose small set expansion is large.
 as a parameter to formalize what it means for the small set expansion of a graph to be large or small. It asserts that, for every
as a parameter to formalize what it means for the small set expansion of a graph to be large or small. It asserts that, for every  , it is
, it is  (good small set expanders), and
(good small set expanders), and  (very far from being a small set expander). Here, the degree
(very far from being a small set expander). Here, the degree  , the best
, the best  . The small set expansion hypothesis, if true, implies that there does not exist an approximation algorithm for this problem with constant approximation ratio. It also can be used to imply the inapproximability of finding a
. The small set expansion hypothesis, if true, implies that there does not exist an approximation algorithm for this problem with constant approximation ratio. It also can be used to imply the inapproximability of finding a  vertices in a
vertices in a  . This is not strong enough to refute the hypothesis; doing so would require finding an algorithm with a bounded approximation ratio.
. This is not strong enough to refute the hypothesis; doing so would require finding an algorithm with a bounded approximation ratio.