
Solid-state nuclear magnetic resonance (ssNMR) is a spectroscopy technique used to characterize atomic-level structure and dynamics in solid materials. ssNMR spectra are broader due to nuclear spin interactions which can be categorized as dipolar coupling, chemical shielding, quadrupolar interactions, and j-coupling. These interactions directly affect the lines shapes of experimental ssNMR spectra which can be seen in powder and dipolar patterns. There are many essential solid-state techniques alongside advanced ssNMR techniques that may be applied to elucidate the fundamental aspects of solid materials. ssNMR is often combined with magic angle spinning (MAS) to remove anisotropic interactions and improve the sensitivity of the technique. The applications of ssNMR further extend to biology and medicine.

Nuclear spin interactions
The resonance frequency of a nuclear spin depends on the strength of the magnetic field at the nucleus, which can be modified by isotropic (e.g. chemical shift, isotropic J-coupling) and anisotropic interactions (e.g. chemical shift anisotropy, dipolar interactions). In a classical liquid-state NMR experiment, molecular tumbling coming from Brownian motion averages anisotropic interactions to zero and they are therefore not reflected in the NMR spectrum. However, in media with no or little mobility (e.g. crystalline powders, glasses, large membrane vesicles, molecular aggregates), anisotropic local fields or interactions have substantial influence on the behaviour of nuclear spins, which results in the line broadening of the NMR spectra.
Chemical shielding
Main article: Chemical shiftChemical shielding is a local property of each nuclear site in a molecule or compound, and is proportional to the applied external magnetic field. The external magnetic field induces currents of the electrons in molecular orbitals. These induced currents create local magnetic fields that lead to characteristic changes in resonance frequency. These changes can be predicted from molecular structure using empirical rules or quantum-chemical calculations.
In general, the chemical shielding is anisotropic because of the anisotropic distribution of molecular orbitals around the nuclear sites. Under sufficiently fast magic angle spinning, or under the effect of molecular tumbling in solution-state NMR, the anisotropic dependence of the chemical shielding is time-averaged to zero, leaving only the isotropic chemical shift.
Dipolar coupling
Main article: Magnetic dipole-dipole interaction
Nuclear spins exhibit a magnetic dipole moment, which generates a magnetic field that interacts with the dipole moments of other nuclei (dipolar coupling). The magnitude of the interaction is dependent on the gyromagnetic ratio of the spin species, the internuclear distance r, and the orientation, with respect to the external magnetic field B, of the vector connecting the two nuclear spins (see figure). The maximum dipolar coupling is given by the dipolar coupling constant d,
- ,
where γ1 and γ2 are the gyromagnetic ratios of the nuclei, is the reduced Planck constant, and is the vacuum permeability. In a strong magnetic field, the dipolar coupling depends on the angle θ between the internuclear vector and the external magnetic field B (figure) according to
- .
D becomes zero for . Consequently, two nuclei with a dipolar coupling vector at an angle of θm = 54.7° to a strong external magnetic field have zero dipolar coupling. θm is called the magic angle. Magic angle spinning is typically used to remove dipolar couplings weaker than the spinning rate.
Quadrupolar interaction
Main article: QuadrupoleNuclei with a spin quantum number >1/2 have a non-spherical charge distribution and a quadrupole moment. The quadrupole moment is a second rank tensor that couples to the surrounding electric field gradient, another second rank tensor. Nuclear quadrupole coupling is typically the second largest interaction in NMR, comparable in size to the largest interaction called Zeeman interactions. When the nuclear quadrupole coupling is not negligible relative to the Zeeman coupling, higher order corrections are needed to describe the NMR spectrum correctly. In such cases, the first-order correction to the NMR transition frequency leads to a strong anisotropic line broadening of the NMR spectrum. However, all symmetric transitions, between and levels are unaffected by the first-order frequency contribution. The second-order frequency contribution depends on the P4 Legendre polynomial, which has zero points at 30.6° and 70.1°. These anisotropic broadenings can be removed using DOR (DOuble angle Rotation) where you spin at two angles at the same time, or DAS (Double Angle Spinning) where you switch quickly between the two angles. Both techniques were developed in the late 1980s, and require specialized hardware (probe). Multiple quantum magic angle spinning (MQMAS) NMR was developed in 1995 and has become a routine method for obtaining high resolution solid-state NMR spectra of quadrupolar nuclei. A similar method to MQMAS is satellite transition magic angle spinning (STMAS) NMR developed in 2000.
J-coupling
The J-coupling or indirect nuclear spin-spin coupling (sometimes also called "scalar" coupling despite the fact that J is a tensor quantity) describes the interaction of nuclear spins through chemical bonds. J-couplings are not always resolved in solids owing to the typically large linewdiths observed in solid state NMR.
Other interactions
Paramagnetic substances are subject to the Knight shift.
Solid-state NMR line shapes
Powder pattern

A powder pattern arises in powdered samples where crystallites are randomly oriented relative to the magnetic field so that all molecular orientations are present. In presence of a chemical shift anisotropy interaction, each orientation with respect to the magnetic field gives a different resonance frequency. If enough crystallites are present, all the different contributions overlap continuously and lead to a smooth spectrum.
Fitting of the pattern in a static ssNMR experiment gives information about the shielding tensor, which are often described by the isotropic chemical shift , the chemical shift anisotropy parameter , and the asymmetry parameter .
Dipolar pattern
Further information: Pake doublet
The dipolar powder pattern (also Pake pattern) has a very characteristic shape that arises when two nuclear spins are coupled together within a crystallite. The splitting between the maxima (the "horns") of the pattern is equal to the dipolar coupling constant .:
where γ1 and γ2 are the gyromagnetic ratios of the dipolar-coupled nuclei, is the internuclear distance, is the reduced Planck constant, and is the vacuum permeability.
Essential solid-state techniques
Magic angle spinning
Main article: Magic angle spinning
Magic angle spinning (MAS) is a technique routinely used in ssNMR to improve ssNMR spectra resolution. After applying the MAS technique, NMR spectra will be sharper and narrower. This improved resolution results from manipulating a sample's spin interactions with the applied magnetic field. This is achieved by rotating the sample at a certain angle to the magnetic field to fully or partially average out anisotropic nuclear interactions such as dipolar, chemical shift anisotropy, and quadrupolar interactions. This rotation angle is called the magic angle θm (ca. 54.74°, where cosθm = 1/3). To achieve the complete averaging of these interactions, the sample needs to be spun at a rate that is at least higher than the largest anisotropy.
Spinning a powder sample at a slower rate than the largest component of the chemical shift anisotropy results in an incomplete averaging of the interaction, and produces a set of spinning sidebands in addition to the isotropic line, centred at the isotropic chemical shift. Spinning sidebands are sharp lines separated from the isotropic frequency by a multiple of the spinning rate. Although spinning sidebands can be used to measure anisotropic interactions, they are often undesirable and removed by spinning the sample faster or by recording the data points synchronously with the rotor period.
Cross-polarization
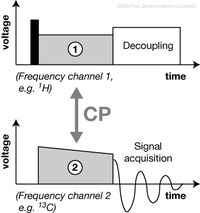
Cross-polarization (CP) if a fundamental (Radiofrequency) RF pulse sequence and a building-block in many solid-state NMR. It is typically used to enhance the signal of a dilute nuclei with a low gyromagnetic ratio (e.g.
C,
N) by magnetization transfer from an abundant nuclei with a high gyromagnetic ratio (e.g.
H), or as a spectral editing method to get through space information (e.g. directed
N→
C CP in protein spectroscopy).
To establish magnetization transfer, RF pulses ("contact pulses") are simultaneously applied on both frequency channels to produce fields whose strength fulfil the Hartmann–Hahn condition:
where are the gyromagnetic ratios, is the spinning rate, and is an integer. In practice, the pulse power, as well as the length of the contact pulse are experimentally optimised. The power of one contact pulse is typically ramped to achieve a more broadband and efficient magnetisation transfer.
Decoupling
Spin interactions can be removed (decoupled) to increase the resolution of NMR spectra during the detection, or to extend the lifetime of the nuclear magnetization.
Heteronuclear decoupling is achieved by radio-frequency irradiation on at the frequency of the nucleus to be decoupled, which is often H. The irradiation can be continuous (continuous wave decoupling), or a series of pulses that extend the performance and the bandwidth of the decoupling (TPPM, SPINAL-64, SWf-TPPM)
Homonuclear decoupling is achieved with multiple-pulse sequences (WAHUHA, MREV-8, BR-24, BLEW-12, FSLG), or continuous wave modulation (DUMBO, eDUMBO). Dipolar interactions can also be removed with magic angle spinning. Ultra fast MAS (from 60 kHz up to above 111 kHz) is an efficient way to average all dipolar interactions, including H–H homonuclear dipolar interactions, which extends the resolution of H spectra and enables the usage of pulse sequences used in solution state NMR.
Advanced solid-state NMR spectroscopy
Rotational Echo DOuble Resonance (REDOR)

Rotational Echo DOuble Resonance (REDOR) experiments, are a type of heteronuclear dipolar recoupling experiment which enables the re-introduction of heteronuclear dipolar couplings averaged by MAS. The reintroduction of such dipolar coupling reduces the intensity of the NMR signal compared to a reference spectrum where no dephasing pulse is used. REDOR can be used to measure heteronuclear distances, and are the basis of NMR crystallographic studies.
Ultra fast MAS for H NMR
The strong H-H homonuclear dipolar interactions associated with broad NMR lines and short T2 relaxation time effectively relegate proton for bimolecular NMR. Fast MAS and reduction of dipolar interactions by deuteration have made proton ssNMR as versatile as in solution. This includes spectral dispersion in multi-dimensional experiments and structurally valuable restraints and parameters important for studying material dynamics.
Ultra-fast NMR and the sharpening of the NMR lines enable NMR pulse sequences to capitalize on proton-detection to improve the sensitivity of the experiments compared to the direct detection of a spin-1/2 system (X). Such enhancement factor is given by:
where are the gyromagnetic ratios, represent the NMR line widths, and represent the quality factor of the probe resonances.
MAS-Dynamic Nuclear Polarisation (MAS-DNP)
Further information: Dynamic nuclear polarizationMagic angle spinning dynamic nuclear polarization (MAS-DNP) is a technique that increases the sensitivity of NMR experiments by several orders of magnitude. It involves transferring the very high electron polarisation from unpaired electrons to nearby nuclei. This is achieved at cryogenic temperatures thorugh a continuous microwave irradiation from a klystron or a gyrotron, with a frequency close to the corresponding electron paramagnetic resonance (EPR) frequency.
The development in the MAS-DNP instrumentation, and the improvement of polarising agents (TOTAPOL, AMUPOL, TEKPOL, etc. ) to achieve a more efficient transfer of polarisation has dramatically reduced experiments times which enabled the observation of surfaces, insensitive isotopes, and multidimensional experiments on low natural abundance nuclei, and diluted species.
Beta-Detected Nuclear Magnetic Resonance (β-NMR)
Beta-detected nuclear magnetic resonance (β-NMR) is specialized technique that has working principles similar to muon spin spectroscopy. It is used in domains such as chemistry, materials science, condensed matter physics, and biology as a powerful probe. β-NMR is practiced at facilities such as TRIUMF and ISOLDE as well as research groups in Osaka and Moscow.
What makes β-NMR different than conventional NMR is firstly, where and when the spin polarization of the nuclei occurs and secondly, how the signal is produced. To conduct a β-NMR experiment, optical pumping is performed on a radioactive beam of particles, such as Li and Mg, to polarize their nuclear spin to nearly one-hundred percent. The isotopes are subsequently implanted into a sample in vacuum in the dilute-limit to eliminate homonuclear probe interactions. The spin–lattice relaxation of the probe is monitored by the parity-violating beta-decay of the radioactive isotope. This anisotropic decay is where the signal originates for β-NMR experiment. This technique allows for investigation of the local magnetic and electronic environment within a material .
Applications
ssNMR spectroscopy serves as an effective analytical tool in biological, organic, and inorganic chemistry due to its close resemblance to liquid-state spectra while providing additional insights into anisotropic interactions.
It is used to characterize chemical composition, structure, local motions, kinetics, and thermodynamics, with the special ability to assign the observed behavior to specific sites in a molecule. It is also crucial in the area of surface and interfacial chemistry.
Biology and Medicine
Proteins and bioaggregates
ssNMR is used to study insoluble proteins and proteins such as membrane proteins and amyloid fibrils. Using the principles of MAS, protein tertiary structure information can be determined. This includes the assessment of protein dynamics.
Biomaterials
ssNMR is used to study biomaterials such as bone, teeth, hair, silk, wood, as well as viruses, plants, cells, and collected biopsies.
Drugs and drug delivery systems
ssNMR is used in pharmaceutical research for the characterization of drug polymorphs and solid dispersions.
Materials science
ssNMR spectroscopy is used in materials science to analyze solid samples. Here, molecules have restricted motion which leads to complex magnetic interactions, such as dipole-dipole coupling, chemical shift anisotropy, and quadrupolar interactions. These interactions can provide more detailed information than X-ray diffraction or solution NMR spectroscopy about the material's structure to elucidate information on the solid's (crystalline and non-crystalline) local structure and dynamics.
ssNMR has been successfully used to study metal organic frameworks, solid-state batteries, surfaces of nanoporous materials, and polymers.
References
- "National Ultrahigh-Field NMR Facility for Solids". Retrieved 2014-09-22.
- ^ "Quadrupolar Coupling". Chemistry LibreTexts. 2013-10-02. Retrieved 2024-12-01.
- Pfeifer, Harry; Barker, Philip (1993). Special Applications. NMR Basic Principles and Progress. Berlin Heidelberg: Springer. ISBN 978-3-642-50048-0.
- "NMR Interactions". Chemistry LibreTexts. 2013-10-02. Retrieved 2024-12-02.
- Qian, Chunqi; Pines, Alex; Martin, Rachel W. (2007-09-01). "Design and construction of a contactless mobile RF coil for double resonance variable angle spinning NMR". Journal of Magnetic Resonance. 188 (1): 183–189. Bibcode:2007JMagR.188..183Q. doi:10.1016/j.jmr.2007.06.006. ISSN 1090-7807. PMID 17638585.
- Frydman Lucio; Harwood John S (1995). "Isotropic Spectra of Half-Integer Quadrupolar Spins from Bidimensional Magic-Angle Spinning NMR". J. Am. Chem. Soc. 117 (19): 5367–5368. doi:10.1021/ja00124a023.
- Massiot D.; Touzo B.; Trumeau D.; Coutures J. P.; Virlet J.; Florian P.; Grandinetti P. J. (1996). "Two-dimensional Magic-Angle Spinning Isotropic Reconstruction Sequences for Quadrupolar Nuclei". Solid-State NMR. 6 (1): 73–83. doi:10.1016/0926-2040(95)01210-9. PMID 8925268.
- ^ Duer, Melinda J. (2004). Introduction to solid-state NMR spectroscopy. Oxford, UK: Blackwell. ISBN 1-4051-0914-9. OCLC 53178681.
- ^ Mehring, Michael (1983). Principles of high resolution NMR in solids (Second, revised and enlarged edition, softcover reprint of the hardcover 2nd edition 1983 ed.). Berlin Heidelberg New York: Springer. ISBN 978-3-642-68758-7.
- ^ Apperley, David C.; Harris, Robin K.; Hodgkinson, Paul (2012). Solid-state NMR: basic principles & practice. New York: Momentum Press, LLC. ISBN 978-1-60650-350-8.
- Hartmann, S. R.; Hahn, E. L. (1962). "Nuclear Double Resonance in the Rotating Frame" (PDF). Phys. Rev. 128 (5): 2042–2053. Bibcode:1962PhRv..128.2042H. doi:10.1103/PhysRev.128.2042.
- Stejskal, E.O; Schaefer, Jacob; Waugh, J.S (October 1977). "Magic-angle spinning and polarization transfer in proton-enhanced NMR". Journal of Magnetic Resonance. 28 (1): 105–112. Bibcode:1977JMagR..28..105S. doi:10.1016/0022-2364(77)90260-8.
- Haeberlen, U.; Waugh, J. S. (1968-11-10). "Coherent Averaging Effects in Magnetic Resonance". Physical Review. 175 (2): 453–467. Bibcode:1968PhRv..175..453H. doi:10.1103/PhysRev.175.453. ISSN 0031-899X.
- Bennett, Andrew E.; Rienstra, Chad M.; Auger, Michèle; Lakshmi, K. V.; Griffin, Robert G. (1995-10-22). "Heteronuclear decoupling in rotating solids". The Journal of Chemical Physics. 103 (16): 6951–6958. Bibcode:1995JChPh.103.6951B. doi:10.1063/1.470372. ISSN 0021-9606.
- Fung, B.M.; Khitrin, A.K.; Ermolaev, Konstantin (2000). "An Improved Broadband Decoupling Sequence for Liquid Crystals and Solids". Journal of Magnetic Resonance. 142 (1): 97–101. Bibcode:2000JMagR.142...97F. doi:10.1006/jmre.1999.1896. PMID 10617439.
- Thakur, Rajendra Singh; Kurur, Narayanan D.; Madhu, P.K. (2006). "Swept-frequency two-pulse phase modulation for heteronuclear dipolar decoupling in solid-state NMR". Chemical Physics Letters. 426 (4–6): 459–463. Bibcode:2006CPL...426..459T. doi:10.1016/j.cplett.2006.06.007.
- Waugh, J. S.; Huber, L. M.; Haeberlen, U. (1968-01-29). "Approach to High-Resolution nmr in Solids". Physical Review Letters. 20 (5): 180–182. Bibcode:1968PhRvL..20..180W. doi:10.1103/PhysRevLett.20.180. ISSN 0031-9007.
- Rhim, W-K.; Elleman, D. D.; Vaughan, R. W. (1973-02-15). "Enhanced resolution for solid state NMR". The Journal of Chemical Physics. 58 (4): 1772–1773. Bibcode:1973JChPh..58.1772R. doi:10.1063/1.1679423. ISSN 0021-9606.
- ^ Burum, D.P; Linder, M; Ernst, R.R (July 1981). "Low-power multipulse line narrowing in solid-state NMR". Journal of Magnetic Resonance. 44 (1): 173–188. Bibcode:1981JMagR..44..173B. doi:10.1016/0022-2364(81)90200-6.
- Lee, Moses; Goldburg, Walter I. (1965-11-15). "Nuclear-Magnetic-Resonance Line Narrowing by a Rotating rf Field". Physical Review. 140 (4A): A1261–A1271. Bibcode:1965PhRv..140.1261L. doi:10.1103/PhysRev.140.A1261.
- Sakellariou, Dimitris; Lesage, Anne; Hodgkinson, Paul; Emsley, Lyndon (March 2000). "Homonuclear dipolar decoupling in solid-state NMR using continuous phase modulation". Chemical Physics Letters. 319 (3–4): 253–260. Bibcode:2000CPL...319..253S. doi:10.1016/S0009-2614(00)00127-5.
- Paruzzo, Federico M.; Emsley, Lyndon (December 2019). "High-resolution 1H NMR of powdered solids by homonuclear dipolar decoupling". Journal of Magnetic Resonance. 309: 106598. Bibcode:2019JMagR.30906598P. doi:10.1016/j.jmr.2019.106598. PMID 31586820. S2CID 203139911.
- Zhang, Rongchun; Mroue, Kamal H.; Ramamoorthy, Ayyalusamy (2017-04-18). "Proton-Based Ultrafast Magic Angle Spinning Solid-State NMR Spectroscopy". Accounts of Chemical Research. 50 (4): 1105–1113. doi:10.1021/acs.accounts.7b00082. ISSN 0001-4842. PMC 5828698. PMID 28353338.
- Struppe, Jochem; Quinn, Caitlin M.; Sarkar, Sucharita; Gronenborn, Angela M.; Polenova, Tatyana (2020-01-13). "Ultrafast 1 H MAS NMR Crystallography for Natural Abundance Pharmaceutical Compounds". Molecular Pharmaceutics. 17 (2): 674–682. doi:10.1021/acs.molpharmaceut.9b01157. ISSN 1543-8384. PMC 7307729. PMID 31891271.
- Gullion T.; Schaefer J. (1989). "Rotational-echo double-resonance NMR". J. Magn. Reson. 81 (2): 196–200. doi:10.1016/j.jmr.2011.09.003. PMID 22152360.
- Schaefer, Jacob (2007-03-15), "REDOR and TEDOR", in Harris, Robin K. (ed.), Encyclopedia of Magnetic Resonance, Chichester, UK: John Wiley & Sons, Ltd, pp. emrstm0448, doi:10.1002/9780470034590.emrstm0448, ISBN 978-0-470-03459-0, retrieved 2021-09-13
- Linser R.; Fink U.; Reif B. (2008). "Proton-Detected Scalar Coupling Based Assignment Strategies in MAS Solid-State NMR Spectroscopy Applied to Perdeuterated Proteins". J. Magn. Reson. 193 (1): 89–93. Bibcode:2008JMagR.193...89L. doi:10.1016/j.jmr.2008.04.021. hdl:11858/00-001M-0000-0018-EE69-A. PMID 18462963.
- Schanda, P.; Meier, B. H.; Ernst, M. (2010). "Quantitative Analysis of Protein Backbone Dynamics in Microcrystalline Ubiquitin by Solid-State NMR Spectroscopy". J. Am. Chem. Soc. 132 (45): 15957–15967. doi:10.1021/ja100726a. PMID 20977205.
- Ishii, Yoshitaka; Wickramasinghe, Ayesha; Matsuda, Isamu; Endo, Yuki; Ishii, Yuji; Nishiyama, Yusuke; Nemoto, Takahiro; Kamihara, Takayuki (2018). "Progress in proton-detected solid-state NMR (SSNMR): Super-fast 2D SSNMR collection for nano-mole-scale proteins". Journal of Magnetic Resonance. 286: 99–109. Bibcode:2018JMagR.286...99I. doi:10.1016/j.jmr.2017.11.011. PMC 6387629. PMID 29223566.
- Lilly Thankamony, Aany Sofia; Wittmann, Johannes J.; Kaushik, Monu; Corzilius, Björn (November 2017). "Dynamic nuclear polarization for sensitivity enhancement in modern solid-state NMR". Progress in Nuclear Magnetic Resonance Spectroscopy. 102–103: 120–195. doi:10.1016/j.pnmrs.2017.06.002. PMID 29157490.
- ^ Rankin, Andrew G.M.; Trébosc, Julien; Pourpoint, Frédérique; Amoureux, Jean-Paul; Lafon, Olivier (2019-09-01). "Recent developments in MAS DNP-NMR of materials". Solid State Nuclear Magnetic Resonance. 101: 116–143. arXiv:2007.09954. doi:10.1016/j.ssnmr.2019.05.009. ISSN 0926-2040. PMID 31189121. S2CID 189814925.
- Rossini, Aaron J.; Zagdoun, Alexandre; Lelli, Moreno; Lesage, Anne; Copéret, Christophe; Emsley, Lyndon (2013-09-17). "Dynamic Nuclear Polarization Surface Enhanced NMR Spectroscopy". Accounts of Chemical Research. 46 (9): 1942–1951. doi:10.1021/ar300322x. ISSN 0001-4842. PMID 23517009.
- Perras, Frédéric A.; Kobayashi, Takeshi; Pruski, Marek (2015-07-08). "Natural Abundance 17 O DNP Two-Dimensional and Surface-Enhanced NMR Spectroscopy". Journal of the American Chemical Society. 137 (26): 8336–8339. doi:10.1021/jacs.5b03905. ISSN 0002-7863. OSTI 1227378. PMID 26098846.
- Smith, Adam N.; Märker, Katharina; Hediger, Sabine; De Paëpe, Gaël (2019-08-15). "Natural Isotopic Abundance 13 C and 15 N Multidimensional Solid-State NMR Enabled by Dynamic Nuclear Polarization". The Journal of Physical Chemistry Letters. 10 (16): 4652–4662. doi:10.1021/acs.jpclett.8b03874. ISSN 1948-7185. PMID 31361489. S2CID 199000068.
- Rossini, Aaron J.; Widdifield, Cory M.; Zagdoun, Alexandre; Lelli, Moreno; Schwarzwälder, Martin; Copéret, Christophe; Lesage, Anne; Emsley, Lyndon (2014-02-12). "Dynamic Nuclear Polarization Enhanced NMR Spectroscopy for Pharmaceutical Formulations". Journal of the American Chemical Society. 136 (6): 2324–2334. doi:10.1021/ja4092038. hdl:20.500.11850/80771. ISSN 0002-7863. PMID 24410528.
- ^ Morris, Gerald D. (2013), "β-NMR", ISAC and ARIEL: The TRIUMF Radioactive Beam Facilities and the Scientific Program, Dordrecht: Springer Netherlands, pp. 173–182, ISBN 978-94-007-7962-4, retrieved 2024-11-29
- Abov, Yu. G.; Gulko, A. D.; Dzheparov, F. S. (2006). "Beta-NMR spectroscopy: Modern state and prospects". Physics of Atomic Nuclei. 69 (10): 1701–1710. doi:10.1134/S106377880610005X. ISSN 1063-7788.
- ^ MacFarlane, W.A. (2015-06-21). "Implanted-ion βNMR: A new probe for nanoscience". Solid State Nuclear Magnetic Resonance. 68–69: 1–12. doi:10.1016/j.ssnmr.2015.02.004.
- ^ Gottberg, Alexander; Stachura, Monika; Kowalska, Magdalena; Bissell, Mark L.; Arcisauskaite, Vaida; Blaum, Klaus; Helmke, Alexander; Johnston, Karl; Kreim, Kim; Larsen, Flemming H.; Neugart, Rainer; Neyens, Gerda; Garcia Ruiz, Ronald F.; Szunyogh, Daniel; Thulstrup, Peter W. (2014-10-09). "Billion-Fold Enhancement in Sensitivity of Nuclear Magnetic Resonance Spectroscopy for Magnesium Ions in Solution". ChemPhysChem. 15 (18): 3929–3932. doi:10.1002/cphc.201402619. ISSN 1439-4235.
- ^ Levy, C. D. P.; Pearson, M. R.; Dehn, M. H.; Karner, V. L.; Kiefl, R. F.; Lassen, J.; Li, R.; MacFarlane, W. A.; McFadden, R. M. L.; Morris, G. D.; Stachura, M.; Teigelhöfer, A.; Voss, A. (2016-11-22). "Development of a polarized 31Mg+ beam as a spin-1/2 probe for BNMR". Hyperfine Interactions. 237 (1): 162. doi:10.1007/s10751-016-1372-8. ISSN 1572-9540.
- Laws, David D. Laws; Bitter, Hans-Marcus L.; Jerschow, Alexej (30 August 2002). "Solid-State NMR Spectroscopic Methods in Chemistry". Angewandte Chemie. 41 (17): 3096. doi:10.1002/1521-3773(20020902)41:17<3096::AID-ANIE3096>3.0.CO;2-X.
- Marchetti, Alessandro; Chen, Juner; Pang, Zhenfeng; Li, Shenhui; Ling, Daishun; Deng, Feng; Kong, Xueqian (April 11, 2017). "Understanding Surface and Interfacial Chemistry in Functional Nanomaterials via Solid-State NMR". Advanced Materials. 29 (14): 1605895. doi:10.1002/adma.201605895. Retrieved 20 December 2023.
- McDermott, Ann (June 2009). "Structure and Dynamics of Membrane Proteins by Magic Angle Spinning Solid-State NMR". Annual Review of Biophysics. 38 (1): 385–403. doi:10.1146/annurev.biophys.050708.133719. ISSN 1936-122X. PMID 19245337.
- Tycko, Robert (2011-05-05). "Solid-State NMR Studies of Amyloid Fibril Structure". Annual Review of Physical Chemistry. 62 (1): 279–299. Bibcode:2011ARPC...62..279T. doi:10.1146/annurev-physchem-032210-103539. ISSN 0066-426X. PMC 3191906. PMID 21219138.
- Linser, Rasmus; Bardiaux, Benjamin; Higman, Victoria; Fink, Uwe; Reif, Bernd (March 2011). "Structure Calculation from Unambiguous Long-Range Amide and Methyl 1H-1H Distance Restraints for a Microcrystalline Protein with MAS Solid-State NMR Spectroscopy". J. Am. Chem. Soc. 133: 5905–5912. doi:10.1021/ja110222h. hdl:11858/00-001M-0000-0018-E916-0.
- Schanda, Paul; Ernst, Matthias (August 2016). "Studying dynamics by magic-angle spinning solid-state NMR spectroscopy: Principles and applications to biomolecules". Prog. Nucl. Magn. Reson. Spectrosc. 96: 1–46. doi:10.1016/j.pnmrs.2016.02.001. PMC 4836562.
- New techniques in solid-state NMR. Jacek Klinowski. Berlin: Springer. 2005. ISBN 978-3-540-22168-5. OCLC 56697027.
{{cite book}}: CS1 maint: others (link) - Duer, Melinda J. (2015). "The contribution of solid-state NMR spectroscopy to understanding biomineralization: Atomic and molecular structure of bone". Journal of Magnetic Resonance. 253: 98–110. Bibcode:2015JMagR.253...98D. doi:10.1016/j.jmr.2014.12.011. PMID 25797009.
- Mohammed, N.R.; Kent, N.W.; Lynch, R.J.M.; Karpukhina, N.; Hill, R.; Anderson, P. (2013). "Effects of Fluoride on in vitro Enamel Demineralization Analyzed by 19F MAS-NMR". Caries Research. 47 (5): 421–428. doi:10.1159/000350171. ISSN 0008-6568. PMID 23712030. S2CID 6854002.
- Ferizoli, Bajram; Cresswell-Boyes, Alexander J.; Anderson, Paul; Lynch, Richard J. M.; Hill, Robert G. (2023-05-24). "Effects of fluoride on in vitro hydroxyapatite demineralisation analysed by 19F MAS-NMR". Frontiers in Dental Medicine. 4. doi:10.3389/fdmed.2023.1171827. ISSN 2673-4915.
- Kricheldorf, H. R.; Müller, D. (1984-11-01). "Secondary structure of peptides 16th. Characterization of proteins by means of13C NMR CP/MAS spectroscopy". Colloid and Polymer Science. 262 (11): 856–861. doi:10.1007/BF01452215. ISSN 1435-1536. S2CID 95774717.
- Zhao, Chenhua; Asakura, Tetsuo (2001-12-14). "Structure of Silk studied with NMR". Progress in Nuclear Magnetic Resonance Spectroscopy. 39 (4): 301–352. doi:10.1016/S0079-6565(01)00039-5. ISSN 0079-6565.
- Gil, A.M.; Neto, C. Pascoal (1999), "Solid-State Nmr Studies Of Wood And Other Lignocellulosic Materials", Annual Reports on NMR Spectroscopy, vol. 37, Elsevier, pp. 75–117, doi:10.1016/s0066-4103(08)60014-9, ISBN 978-0-12-505337-2, retrieved 2021-09-13
- Quinn, Caitlin M.; Lu, Manman; Suiter, Christopher L.; Hou, Guangjin; Zhang, Huilan; Polenova, Tatyana (2015). "Magic angle spinning NMR of viruses". Progress in Nuclear Magnetic Resonance Spectroscopy. 86–87: 21–40. doi:10.1016/j.pnmrs.2015.02.003. PMC 4413014. PMID 25919197.
- Mandala, Venkata S.; McKay, Matthew J.; Shcherbakov, Alexander A.; Dregni, Aurelio J.; Kolocouris, Antonios; Hong, Mei (2020). "Structure and drug binding of the SARS-CoV-2 envelope protein transmembrane domain in lipid bilayers". Nature Structural & Molecular Biology. 27 (12): 1202–1208. doi:10.1038/s41594-020-00536-8. ISSN 1545-9993. PMC 7718435. PMID 33177698.
- Wang, Tuo; Hong, Mei (2016). "Solid-state NMR investigations of cellulose structure and interactions with matrix polysaccharides in plant primary cell walls". Journal of Experimental Botany. 67 (2): 503–514. doi:10.1093/jxb/erv416. ISSN 0022-0957. PMC 6280985. PMID 26355148.
- Zhao, Wancheng; Fernando, Liyanage D.; Kirui, Alex; Deligey, Fabien; Wang, Tuo (2020). "Solid-state NMR of plant and fungal cell walls: A critical review". Solid State Nuclear Magnetic Resonance. 107: 101660. doi:10.1016/j.ssnmr.2020.101660. PMID 32251983. S2CID 215409770.
- Renault, M.; Tommassen-van Boxtel, R.; Bos, M. P.; Post, J. A.; Tommassen, J.; Baldus, M. (2012-03-27). "Cellular solid-state nuclear magnetic resonance spectroscopy". Proceedings of the National Academy of Sciences. 109 (13): 4863–4868. doi:10.1073/pnas.1116478109. ISSN 0027-8424. PMC 3323964. PMID 22331896.
- Renault, Marie; Pawsey, Shane; Bos, Martine P.; Koers, Eline J.; Nand, Deepak; Tommassen-van Boxtel, Ria; Rosay, Melanie; Tommassen, Jan; Maas, Werner E.; Baldus, Marc (2012-03-19). "Solid-State NMR Spectroscopy on Cellular Preparations Enhanced by Dynamic Nuclear Polarization". Angewandte Chemie International Edition. 51 (12): 2998–3001. doi:10.1002/anie.201105984. PMID 22298470.
- Martínez-Bisbal, M. Carmen; Martí-Bonmatí, Luis; Piquer, José; Revert, Antonio; Ferrer, Pilar; Llácer, José L.; Piotto, Martial; Assemat, Olivier; Celda, Bernardo (2004). "1H and13C HR-MAS spectroscopy of intact biopsy samplesex vivo andin vivo1H MRS study of human high grade gliomas". NMR in Biomedicine. 17 (4): 191–205. doi:10.1002/nbm.888. ISSN 0952-3480. PMID 15229932. S2CID 19939314.
- Li, Mingyue; Xu, Wei; Su, Yongchao; Su, Yongchao (December 2020). "Solid-state NMR Spectroscopy in Pharmaceutical Sciences". TrAC Trends in Analytical Chemistry. 135 (4): 116152. doi:10.1016/j.trac.2020.116152.
- Brunner, Eike; Rauche, Marcus (2020). "Solid-state NMR spectroscopy: an advancing tool to analyse the structure and properties of metal-organic frameworks". Chemical Science. 11 (6): 9880–9891. doi:10.1039/D0SC00735H. PMC 8159446.
- Borisov, A.S., Hazendonk, P. & Hayes, P.G. Solid-State Nuclear Magnetic Resonance Spectroscopy: A Review of Modern Techniques and Applications for Inorganic Polymers. J Inorg Organomet Polym 20, 183–212 (2010). https://doi.org/10.1007/s10904-010-9358-5
- Hoffmann, Herbert; Debowski, Marta; Müller, Philipp; Paasch, Silvia; Senkovska, Irena; Kaskel, Stefan; Brunner, Eike (2012-11-28). "Solid-State NMR Spectroscopy of Metal–Organic Framework Compounds (MOFs)". Materials. 5 (12): 2537–2572. Bibcode:2012Mate....5.2537H. doi:10.3390/ma5122537. ISSN 1996-1944. PMC 5449066.
- Blanc, Frédéric; Leskes, Michal; Grey, Clare P. (2013-09-17). "In Situ Solid-State NMR Spectroscopy of Electrochemical Cells: Batteries, Supercapacitors, and Fuel Cells". Accounts of Chemical Research. 46 (9): 1952–1963. doi:10.1021/ar400022u. ISSN 0001-4842. PMID 24041242.
- Pinto, Moisés L.; Mafra, Luís; Guil, José M.; Pires, João; Rocha, João (2011-03-22). "Adsorption and Activation of CO 2 by Amine-Modified Nanoporous Materials Studied by Solid-State NMR and 13 CO 2 Adsorption". Chemistry of Materials. 23 (6): 1387–1395. doi:10.1021/cm1029563. ISSN 0897-4756.
- Schmidt-Rohr, K. (1994). Multidimensional solid-state NMR and polymers. Hans Wolfgang Spiess. London: Academic Press. ISBN 0-12-626630-1. OCLC 31785818.
Suggested readings for beginners
General NMR
- Keeler, James (2002). "Understanding NMR Spectroscopy". Apollo-University Of Cambridge Repository, Apollo-University Of Cambridge Repository. doi:10.17863/CAM.968.
- Hore, P. J. (2015). NMR : the toolkit : how pulse sequences work. J. A. Jones, Stephen Wimperis (2nd ed.). Oxford. ISBN 978-0-19-870342-6. OCLC 910929523.
{{cite book}}: CS1 maint: location missing publisher (link) - Hore, P. J. (2015). Nuclear magnetic resonance (2nd ed.). Oxford. ISBN 978-0-19-870341-9. OCLC 910929524.
{{cite book}}: CS1 maint: location missing publisher (link) - Encyclopedia of NMR. Robin K. Harris, Roderick E. Wasylishen. Chichester, West Sussex: John Wiley & Sons. 2012. ISBN 978-0-470-05821-3. OCLC 796758664.
{{cite book}}: CS1 maint: others (link)
Solid-state NMR
- Laws David D., Hans- , Bitter Marcus L., Jerschow Alexej (2002). "Solid-State NMR Spectroscopic Methods in Chemistry". Angewandte Chemie International Edition. 41 (17): 3096–3129. doi:10.1002/1521-3773(20020902)41:17<3096::AID-ANIE3096>3.0.CO;2-X. PMID 12207374.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - Reif, Bernd; Ashbrook, Sharon E.; Emsley, Lyndon; Hong, Mei (2021). "Solid-state NMR spectroscopy". Nature Reviews Methods Primers. 1. doi:10.1038/s43586-020-00002-1. PMC 8341432. PMID 34368784.
- Levitt, Malcolm H., Spin Dynamics: Basics of Nuclear Magnetic Resonance, Wiley, Chichester, United Kingdom, 2001. ISBN 978-0470511176 (NMR basics, including solids)
- Duer, Melinda J., Introduction to Solid-State NMR Spectroscopy, Blackwell, Oxford, 2004. (Some detailed examples of ssNMR spectroscopy)
- Schmidt-Rohr, K. and Spiess, H.-W., Multidimensional Solid-State NMR and Polymers, Academic Press, San Diego, 1994.
External links
- mrsimulator Python package for simulating solid-state NMR spectra.
- SSNMRBLOG Solid-State NMR Literature Blog by Prof. Rob Schurko's Solid-State NMR group at the University of Windsor
- "Solid-State MAS NMR | Protein NMR". Retrieved 2021-09-13.
- "University of Ottawa NMR Facility Blog". u-of-o-nmr-facility.blogspot.com. Retrieved 2021-09-13.
| Spectroscopy | |||||||
|---|---|---|---|---|---|---|---|
| Vibrational (IR) | |||||||
| UV–Vis–NIR "Optical" | |||||||
| X-ray and Gamma ray | |||||||
| Electron | |||||||
| Nucleon | |||||||
| Radiowave | |||||||
| Others |
| ||||||
| NMR spectroscopy by isotope | |
|---|---|
| Isotope | |
 ,
, is the
is the  is the
is the  .
. . Consequently, two nuclei with a dipolar coupling vector at an angle of θm = 54.7° to a strong external magnetic field have zero dipolar coupling. θm is called the
. Consequently, two nuclei with a dipolar coupling vector at an angle of θm = 54.7° to a strong external magnetic field have zero dipolar coupling. θm is called the  and
and  levels are unaffected by the first-order frequency contribution. The second-order frequency contribution depends on the P4
levels are unaffected by the first-order frequency contribution. The second-order frequency contribution depends on the P4  and chemical shift anisotropy
and chemical shift anisotropy  parameters.
parameters. , the chemical shift anisotropy parameter
, the chemical shift anisotropy parameter  .:
.:
 is the internuclear distance,
is the internuclear distance,  fields whose strength fulfil the Hartmann–Hahn condition:
fields whose strength fulfil the Hartmann–Hahn condition:

 are the
are the  is the spinning rate, and
is the spinning rate, and  is an integer. In practice, the pulse power, as well as the length of the contact pulse are experimentally optimised. The power of one contact pulse is typically ramped to achieve a more broadband and efficient magnetisation transfer.
is an integer. In practice, the pulse power, as well as the length of the contact pulse are experimentally optimised. The power of one contact pulse is typically ramped to achieve a more broadband and efficient magnetisation transfer.
 is given by:
is given by:

 represent the NMR line widths, and
represent the NMR line widths, and  represent the
represent the