Misplaced Pages

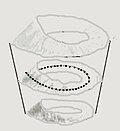
In mathematics, a solid Klein bottle is a three-dimensional topological space (a 3-manifold) whose boundary is the Klein bottle.

It is homeomorphic to the quotient space obtained by gluing the top disk of a cylinder ${\displaystyle \scriptstyle D^{2}\times I}$ to the bottom disk by a reflection across a diameter of the disk.

Alternatively, one can visualize the solid Klein bottle as the trivial product ${\displaystyle \scriptstyle M{\ddot {o}}\times I}$, of the möbius strip and an interval ${\displaystyle \scriptstyle I=}$. In this model one can see that the core central curve at 1/2 has a regular neighbourhood which is again a trivial cartesian product: ${\displaystyle \scriptstyle M{\ddot {o}}\times }$ and whose boundary is a Klein bottle.

4D Visualization Through a Cylindrical Transformation

One approach to conceptualizing the solid klein bottle in four-dimensional space involves imagining a cylinder, which appears flat to a hypothetical four-dimensional observer. The cylinder possesses distinct "top" and "bottom" four-dimensional surfaces. By introducing a half-twist along the fourth dimension and subsequently merging the ends, the cylinder undergoes a transformation. While the total volume of the object remains unchanged, the resulting structure possesses a singular continuous four-dimensional surface, analogous to the way a Möbius strip has one continuous two-dimensional surface in three-dimensional space, and a regular 2d manifold klein bottle as the boundary.

References

1. Carter, J. Scott (1995), How Surfaces Intersect in Space: An Introduction to Topology, K & E series on knots and everything, vol. 2, World Scientific, p. 169, ISBN 9789810220662.

This topology-related article is a stub. You can help Misplaced Pages by expanding it.

• v
• t
• e

• 3-manifolds
• Topology stubs