Misplaced Pages

The concept of a spatial weight is used in spatial analysis to describe neighbor relations between regions on a map. If location ${\displaystyle i}$ is a neighbor of location ${\displaystyle j}$ then ${\displaystyle w_{ij}\neq 0}$ otherwise ${\displaystyle w_{ij}=0}$. Usually (though not always) we do not consider a site to be a neighbor of itself so ${\displaystyle w_{ii}=0}$. These coefficients are encoded in the spatial weight matrix

${\displaystyle W={\begin{pmatrix}w_{11}&w_{12}&\ldots &w_{1N}\\w_{21}&w_{22}&\ldots &w_{2N}\\\vdots &\vdots &\vdots &\vdots \\w_{N1}&w_{N2}&\ldots &w_{NN}\\\end{pmatrix}}}$

Where ${\displaystyle N}$ is the number of sites under consideration. The spatial weight matrix is a key quantity in the computation of many spatial indices like Moran's I, Geary's C, Getis-Ord statistics and Join Count Statistics.

Contiguity-Based Weights

This approach considers spatial sites as nodes in a graph with links determined by a shared boundary or vertex. The elements of the spatial weight matrix are determined by setting ${\displaystyle w_{ij}=1}$ for all connected pairs of nodes ${\displaystyle ij}$ with all the other elements set to 0. This makes the spatial weight matrix equivalent to the adjacency matrix of the corresponding network. It is common to row-normalize the matrix ${\displaystyle W}$,

${\displaystyle w_{ij}\rightarrow w_{ij}/\sum _{j}w_{ij}}$

In this case the sum of all the elements of ${\displaystyle W}$ equals ${\displaystyle N}$ the number of sites.

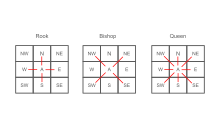
There are three common methods for linking sites named after the chess pieces which make similar moves:

• Rook: sites are neighbors if they share an edge
• Bishop: sites are neighbours if they share a vertex
• Queen: sites are neighbours if they share an edge or a vertex

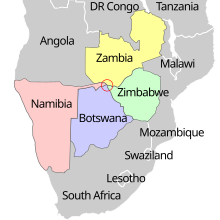
In some cases statistics can be quite different depending on the definition used, especially for discrete data on a grid. There are also other cases where the choice of neighbors is not obvious and can affect the outcome of the analysis. Bivand and Wong describe a situation where the value of spatial indices of association (like Moran's I) depend on the inclusion or exclusion of a ferry crossing between counties. There are also cases where regions meet in a tripoint or quadripoint where Rook and Queen neighborhoods can differ.

Distance-Based Weights

Another way to define spatial neighbors is based on the distance between sites. One simple choice is to set ${\displaystyle w_{ij}=1}$ for every pair ${\displaystyle (i,j)}$ separated by a distance less than some threshold ${\displaystyle \delta }$. Cliff and Ord suggest the general form

${\displaystyle w_{ij}=g(d_{ij},\beta _{ij})}$

Where ${\displaystyle g}$ is some function of ${\displaystyle d_{ij}}$ the distance between ${\displaystyle i}$ and ${\displaystyle j}$ and ${\displaystyle \beta _{ij}}$ is the proportion of the perimeter of ${\displaystyle i}$ in contact with ${\displaystyle j}$. The function

${\displaystyle w_{ij}=d_{ij}^{-\alpha }\beta _{ij}^{b}}$

is then suggested. Often the ${\displaystyle \beta }$ term is not included and the most common values for ${\displaystyle \alpha }$ are 1 and 2. Another common choice for the distance decay function is

${\displaystyle w_{ij}=\exp(-d_{ij})}$

though a number of different Kernel functions can be used. The exponential and other Kernel functions typically set ${\displaystyle w_{ii}=1}$ which must be considered in applications.

It is possible to make the spatial weight matrix a function of 'distance class': ${\displaystyle w_{ij}\rightarrow w_{ij}(d)}$ where ${\displaystyle d}$ denotes the 'distance class', for example ${\displaystyle d=1,2,3,\ldots }$ corresponding to first, second, third etc. neighbors. In this case, functions of the spatial weight matrix become distance class dependent. For example, Moran's I is

${\displaystyle I(d)={\frac {N}{|W(d)|}}{\frac {\sum _{i=1}^{N}\sum _{j=1}^{N}w_{ij}(d)(x_{i}-{\bar {x}})(x_{j}-{\bar {x}})}{\sum _{i=1}^{N}(x_{i}-{\bar {x}})^{2}}}}$

This defines a type of spatial correlogram, in this case, since Moran's I measures spatial autocorrelation, ${\displaystyle I(d)}$ measures how the autocorrelation of the data changes as a function of distance class. Remembering Tobler's first law of geography, "everything is related to everything else, but near things are more related than distant things" it usually decreases with distance.

Common distance functions include Euclidean distance, Manhattan distance and Great-circle distance.

Spatial Lag

One application of the spatial weight matrix is to compute the spatial lag

${\displaystyle _{i}=\sum _{j}w_{ij}x_{j}}$

For row-standardised weights initially set to ${\displaystyle w_{ij}=1}$ and with ${\displaystyle w_{ii}=0}$, ${\displaystyle _{i}}$ is simply the average value observed at the neighbors of ${\displaystyle i}$. These lagged variables can then be used in regression analysis to incorporate the dependence of the outcome variable on the values at neighboring sites. The standard regression equation is

${\displaystyle y_{i}=\sum _{k}x_{ik}\beta _{k}+\epsilon _{i}}$

The spatial lag model adds the spatial lag vector to this

${\displaystyle y_{i}=\rho \sum _{j}w_{ij}y_{j}+\sum _{k}x_{ik}\beta _{k}+\epsilon _{i}}$

where ${\displaystyle \rho }$ is a parameter which controls the degree of autocorrelation of ${\displaystyle y}$. This is similar to an autoregressive model in the analysis of time series.

See Also

• Spatial Analysis
• Moran's I
• Geary's C
• Join Count Statistics

References

1. ^ Cliff, A.D. and Ord, J.K. (1981). Spatial Processes: Models & Applications. Pion. ISBN 9780850860818.{{cite book}}: CS1 maint: multiple names: authors list (link)
2. ^ "Contiguity-Based Spatial Weights".
3. ^ Dale MR, Fortin MJ. Spatial analysis: a guide for ecologists. Cambridge University Press; 2014 Sep 11.
4. Bivand RS, Wong DW. Comparing implementations of global and local indicators of spatial association. Test. 2018 Sep;27(3):716-48.
5. ^ "Distance-Band Spatial Weights".
6. "Spatial Weights as Distance Functions".
7. Legendre P, Legendre L. Numerical ecology. Elsevier; 2012 Jul 21.
8. "Applications of Spatial Weights".
9. Anselin L, Griffith DA. Do spatial effecfs really matter in regression analysis?. Papers in Regional Science. 1988 Jan 1;65(1):11-34.
10. Seya H, Yoshida T, Yamagata Y. Spatial econometric models. InSpatial Analysis Using Big Data 2020 Jan 1 (pp. 113-158). Academic Press.

• Spatial analysis
• Covariance and correlation