

A split-ring resonator (SRR) is an artificially produced structure common to metamaterials. Its purpose is to produce the desired magnetic susceptibility (magnetic response) in various types of metamaterials up to 200 terahertz.
Background
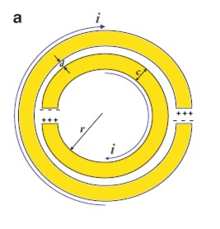
Split ring resonators (SRRs) consist of a pair of concentric metallic rings, etched on a dielectric substrate, with slits etched on opposite sides. SRRs can produce the effect of being electrically smaller when responding to an oscillating electromagnetic field. These resonators have been used for the synthesis of left-handed and negative refractive index media, where the necessary value of the negative effective permeability is due to the presence of the SRRs. When an array of electrically small SRRs is excited by means of a time-varying magnetic field, the structure behaves as an effective medium with negative effective permeability in a narrow band above SRR resonance. SRRs have also been coupled to planar transmission lines for the synthesis of metamaterials transmission line. These media create the necessary strong magnetic coupling to an applied electromagnetic field not otherwise available in conventional materials. For example, an effect such as negative permeability is produced with a periodic array of split ring resonators.
A single-cell SRR has a pair of enclosed loops with splits in them at opposite ends. The loops are made of nonmagnetic metal like copper and have a small gap between them. The loops can be concentric or square, and gapped as needed. A magnetic flux penetrating the metal rings will induce rotating currents in the rings, which produce their own flux to enhance or oppose the incident field (depending on the SRR resonant properties). This field pattern is dipolar. The small gaps between the rings produces large capacitance values, which lowers the resonating frequency. Hence the dimensions of the structure are small compared to the resonant wavelength. This results in low radiative losses and very high quality factors.
The split ring resonator was a microstructure design featured in the paper by Pendry et al in 1999 called, "Magnetism from Conductors and Enhanced Nonlinear Phenomena". It proposed that the split ring resonator design, built out of nonmagnetic material, could enhance the magnetic activity unseen in natural materials. In the simple microstructure design, it is shown that in an array of conducting cylinders, with an applied external field parallel to the cylinders, the effective permeability can be written as the following. (This model is very limited and the effective permeability cannot be less than zero or greater than one.)
Where is the resistance of the cylinder surface per unit area, a is the spacing of the cylinders, is the angular frequency, is the permeability of free space and r is the radius. Moreover, when gaps are introduced to a double cylinder design similar to the image above, we see that the gaps produce a capacitance. This capacitor and inductor microstructure design introduces a resonance that amplifies the magnetic effect. The new form of the effective permeability resembles a familiar response known in plasmonic materials.
Where d is the spacing of the concentric conducting sheets. The final design replaces the double concentric cylinders with a pair of flat concentric c-shaped sheets, placed on each side of a unit cell. The unit cells are stacked on top of each other by a length, l. The final result of the effective permeability can be seen below.
where c is the thickness of the c-shaped sheet and is the resistance of unit length of the sheets measured around the circumference.
Characteristics
The split ring resonator and the metamaterial itself are composite materials. Each SRR has an individual tailored response to the electromagnetic field. However, the periodic construction of many SRR cells is such that the electromagnetic wave interacts as if these were homogeneous materials. This is similar to how light actually interacts with everyday materials; materials such as glass or lenses are made of atoms, an averaging or macroscopic effect is produced.
The SRR is designed to mimic the magnetic response of atoms, only on a much larger scale. Also, as part of periodic composite structure, the SRR is designed to have a stronger magnetic coupling than is found in nature. The larger scale allows for more control over the magnetic response, while each unit is smaller than the radiated electromagnetic wave.
SRRs are much more active than ferromagnetic materials found in nature. The pronounced magnetic response in such lightweight materials demonstrates an advantage over heavier, naturally occurring materials. Each unit can be designed to have its own magnetic response. The response can be enhanced or lessened as desired. In addition, the overall effect reduces power requirements.
SRR configuration
There are a variety of split-ring resonators and periodic structures: rod-split-rings, nested split-rings, single split rings, deformed split-rings, spiral split-rings, and extended S-structures. The variations of split ring resonators have achieved different results, including smaller and higher frequency structures. The research which involves some of these types are discussed throughout the article.
To date (December 2009) the capability for desired results in the visible spectrum has not been achieved. However, in 2005 it was noted that, physically, a nested circular split-ring resonator must have an inner radius of 30 to 40 nanometers for success in the mid-range of the visible spectrum. Microfabrication and nanofabrication techniques may utilize direct laser beam writing or electron beam lithography depending on the desired resolution.
Various configurations
| This section's tone or style may not reflect the encyclopedic tone used on Misplaced Pages. See Misplaced Pages's guide to writing better articles for suggestions. (October 2017) (Learn how and when to remove this message) |

Split-ring resonators (SRR) are one of the most common elements used to fabricate metamaterials. Split-ring resonators are non-magnetic materials, which initially were fabricated from circuit board material to create metamaterials.
Looking at the image directly to the right, it can be seen that at first a single SRR looks like an object with two square perimeters, with each perimeter having a small section removed. This results in square "C" shapes on fiberglass printed circuit board material. In this type of configuration it is actually two concentric bands of non-magnetic conductor material. There is one gap in each band placed 180° relative to each other. The gap in each band gives it the distinctive "C" shape, rather than a totally circular or square shape. Then multiple cells of this double band configuration are fabricated onto circuit board material by an etching technique and lined with copper wire strip arrays. After processing, the boards are cut and assembled into an interlocking unit. It is constructed into a periodic array with a large number of SRRs.
There are now a number of different configurations that use the SRR nomenclature.
Demonstrations
A periodic array of SRRs was used for the first demonstration of a negative index of refraction. For this demonstration, square shaped SRRs, with the lined wire configurations, were fabricated into a periodic, arrayed, cell structure. This is the substance of the metamaterial. Then a metamaterial prism was cut from this material. The prism experiment demonstrated a negative index of refraction for the first time in the year 2000; the paper about the demonstration was submitted to the journal Science on January 8, 2001, accepted on February 22, 2001 and published on April 6, 2001.
Just before this prism experiment, Pendry et al. was able to demonstrate that a three-dimensional array of intersecting thin wires could be used to create negative values of ε. In a later demonstration, a periodic array of copper split-ring resonators could produce an effective negative μ. In 2000 Smith et al. were the first to successfully combine the two arrays and produce a so-called left-handed material, which has negative values of ε and μ for a band of frequencies in the GHz range.
SRRs were first used to fabricate left-handed metamaterials for the microwave range, and several years later for the terahertz range. By 2007, experimental demonstration of this structure at microwave frequencies has been achieved by many groups. In addition, SRRs have been used for research in acoustic metamaterials. The arrayed SRRs and wires of the first left-handed metamaterial were melded into alternating layers. This concept and methodology was then applied to (dielectric) materials with optical resonances producing negative effective permittivity for certain frequency intervals resulting in "photonic bandgap frequencies". Another analysis showed left-handed materials to be fabricated from inhomogeneous constituents, which yet results in a macroscopically homogeneous material. SRRs had been used to focus a signal from a point source, increasing the transmission distance for near field waves. Furthermore, another analysis showed SRRs with a negative index of refraction capable of high-frequency magnetic response, which created an artificial magnetic device composed of non-magnetic materials (dielectric circuit board).
The resonance phenomena that occurs in this system is essential to achieving the desired effects.
SRRs also exhibit resonant electric response in addition to their resonant magnetic response. The response, when combined with an array of identical wires, is averaged over the whole composite structure which results in effective values, including the refractive index. The original logic behind SRRs specifically, and metamaterials generally was to create a structure, which imitates an arrayed atomic structure only on a much larger scale.
Several types of SRR
In research based in metamaterials, and specifically negative refractive index, there are different types of split-ring resonators. Of the examples mentioned below, most of them have a gap in each ring. In other words, with a double ring structure, each ring has a gap.
There is the 1-D Split-Ring Structure with two square rings, one inside the other. One set of cited "unit cell" dimensions would be an outer square of 2.62 mm and an inner square of 0.25 mm. 1-D structures such as this are easier to fabricate compared with constructing a rigid 2-D structure.
The Symmetrical-Ring Structure is another classic example. Described by the nomenclature these are two rectangular square D type configurations, exactly the same size, lying flat, side by side, in the unit cell. Also these are not concentric. One set of cited dimensions are 2 mm on the shorter side, and 3.12 mm on the longer side. The gaps in each ring face each other, in the unit cell.
The Omega Structure, as the nomenclature describes, has an Ω-shaped ring structure. There are two of these, standing vertical, side by side, instead of lying flat, in the unit cell. In 2005 these were considered to be a new type of metamaterial. One set of cited dimensions are annular parameters of R=1.4 mm and r=1 mm, and the straight edge is 3.33 mm.
Another new metamaterial in 2005 was a coupled S-shaped structure. There are two vertical S-shaped structures, side by side, in a unit cell. There is no gap as in the ring structure; however, there is a space between the top and middle parts of the S and space between the middle part and bottom part of the S. Furthermore, it still has the properties of having an electric plasma frequency and a magnetic resonant frequency.
Research
On May 1, 2000, research was published about an experiment which involved conducting wires placed symmetrically within each cell of a periodic split-ring resonator array. This effectively achieved negative permeability and permittivity for electromagnetic waves in the microwave regime. The concept was and still is used to build interacting elements smaller than the applied electromagnetic radiation. In addition, the spacing between the resonators is much smaller than the wavelength of the applied radiation.
Additionally, the splits in the ring allow the SRR unit to achieve resonance at wavelengths much larger than the diameter of the ring. The unit is designed to generate a large capacitance, lower the resonant frequency, and concentrate the electric field. Combining units creates a design as a periodic medium. Furthermore, the multiple unit structure has strong magnetic coupling with low radiative losses. Research has also covered variations in magnetic resonances for different SRR configurations. Research has continued into terahertz radiations with SRRs Other related work fashioned metamaterial configurations with fractals and non-SRR structures. These can be constructed with materials such as periodic metallic crosses, or an ever-widening concentric ring structures known as Swiss rolls. Permeability for only the red wavelength at 780 nm has been analyzed and along with other related work.
See also
- History of metamaterials
- Superlens
- Quantum metamaterials
- Metamaterial cloaking
- Photonic metamaterials
- Metamaterial antennas
- Nonlinear metamaterials
- Photonic crystal
- Seismic metamaterials
- Acoustic metamaterials
- Metamaterial absorber
- Plasmonic metamaterials
- Terahertz metamaterials
- Tunable metamaterials
- Transformation optics
- Theories of cloaking
- Academic journals
- Metamaterials books
References
- ^ Smith, D. R.; Padilla, WJ; Vier, DC; Nemat-Nasser, SC; Schultz, S (2000). "Composite Medium with Simultaneously Negative Permeability and Permittivity". Physical Review Letters. 84 (18): 4184–7. Bibcode:2000PhRvL..84.4184S. doi:10.1103/PhysRevLett.84.4184. PMID 10990641.
- Shelby, R. A.; Smith, D. R.; Nemat-Nasser, S. C.; Schultz, S. (2001). "Microwave transmission through a two-dimensional, isotropic, left-handed metamaterial". Applied Physics Letters. 78 (4): 489. Bibcode:2001ApPhL..78..489S. doi:10.1063/1.1343489.
- Degl’Innocenti, R. (2014). "Low-Bias Terahertz Amplitude Modulator Based on Split-Ring Resonators and Graphene". ACS Nano. 8 (3): 2548–2554. doi:10.1021/nn406136c. PMID 24558983.
- Naqui, Jordi; Durán-Sindreu, Miguel; Martín, Ferran (2011). "Novel Sensors Based on the Symmetry Properties of Split Ring Resonators (SRRs)". Sensors. 11 (12): 7545–7553. Bibcode:2011Senso..11.7545N. doi:10.3390/s110807545. ISSN 1424-8220. PMC 3231717. PMID 22164031.
- ^ Pendry, J.B.; Holden, A.J.; Robbins, D.J.; Stewart, W.J. (1999). "Magnetism from conductors and enhanced nonlinear phenomena". IEEE Transactions on Microwave Theory and Techniques. 47 (11): 2075–2084. Bibcode:1999ITMTT..47.2075P. CiteSeerX 10.1.1.564.7060. doi:10.1109/22.798002. ISSN 0018-9480.
- Smith, D.; Padilla, Willie; Vier, D.; Nemat-Nasser, S.; Schultz, S. (2000). "Composite Medium with Simultaneously Negative Permeability and Permittivity". Physical Review Letters. 84 (18): 4184–4187. Bibcode:2000PhRvL..84.4184S. doi:10.1103/PhysRevLett.84.4184. ISSN 0031-9007. PMID 10990641.
- Shelby, R. A. (2001). "Experimental Verification of a Negative Index of Refraction". Science. 292 (5514): 77–79. Bibcode:2001Sci...292...77S. CiteSeerX 10.1.1.119.1617. doi:10.1126/science.1058847. ISSN 0036-8075. PMID 11292865. S2CID 9321456.
- ^ Gay-Balmaz, Philippe; Martin, Olivier J. F. (2002). "Electromagnetic resonances in individual and coupled split-ring resonators" (free PDF download). Journal of Applied Physics. 92 (5): 2929. Bibcode:2002JAP....92.2929G. doi:10.1063/1.1497452.
- Baena, J.D.; Bonache, J.; Martin, F.; Sillero, R.M.; Falcone, F.; Lopetegi, T.; Laso, M.A.G.; Garcia-Garcia, J.; et al. (2005). "Equivalent-circuit models for split-ring resonators and complementary split-ring resonators coupled to planar transmission lines" (PDF). IEEE Transactions on Microwave Theory and Techniques. 53 (4): 1451–1461. Bibcode:2005ITMTT..53.1451B. doi:10.1109/TMTT.2005.845211. S2CID 18406919. Archived from the original (free PDF download) on October 14, 2009.
- Marqués, R.; Martel, J.; Mesa, F.; Medina, F. (2002). "Left-Handed-Media Simulation and Transmission of EM Waves in Subwavelength Split-Ring-Resonator-Loaded Metallic Waveguides" (PDF). Physical Review Letters. 89 (18): 183901. Bibcode:2002PhRvL..89r3901M. doi:10.1103/PhysRevLett.89.183901. hdl:11441/62810. PMID 12398601. S2CID 32685189. Archived from the original (free PDF download) on October 14, 2009.
- John Brian Pendry; Anthony J. Holden; D. J. Robbins; William James Stewart (1999). "Magnetism from conductors and enhanced nonlinear phenomena". IEEE Transactions on Microwave Theory and Techniques. 47 (11): 2075–2084. Bibcode:1999ITMTT..47.2075P. doi:10.1109/22.798002.
- Parsons, J.; Hendry, E.; Sambles, J. R.; Barnes, W. L. (2009-12-23). "Localized surface-plasmon resonances and negative refractive index in nanostructured electromagnetic metamaterials". Physical Review B. 80 (24): 245117. Bibcode:2009PhRvB..80x5117P. doi:10.1103/PhysRevB.80.245117. ISSN 1098-0121.
-
Pendry, John B.; AJ Holden; DJ Robbins; WJ Stewart (1999-02-03). "Magnetism from Conductors, and Enhanced Non-Linear Phenomena" (PDF). IEEE Trans. Microw. Theory Tech. 47 (11): 2075–2084. Bibcode:1999ITMTT..47.2075P. CiteSeerX 10.1.1.564.7060. doi:10.1109/22.798002. Archived from the original (Free PDF download. Cited by 2,136 articles. Alternate PDF here Nov. 1999) on 2011-07-17. Retrieved 2009-12-10.
{{cite journal}}: External link in|format= - ^ Moser, H.O.; et al. (2005-07-08). Electromagnetic metamaterials over the whole THz range – achievements and perspectives (Free PDF download, click on link.). p. 18. doi:10.1142/9789812701718_0003. ISBN 978-981-256-411-5. Retrieved 2009-10-21.
{{cite book}}:|journal=ignored (help) - Shelby, R. A.; Smith D.R.; Shultz S.; Nemat-Nasser S.C. (2001). "Microwave transmission through a two-dimensional, isotropic, left-handed metamaterial" (PDF). Applied Physics Letters. 78 (4): 489. Bibcode:2001ApPhL..78..489S. doi:10.1063/1.1343489.
- ^ Lee, Yun-Shik (2008). Principles of Terahertz Science and Technology. Vol. Lecture Notes in Physics. New York: Springer-Verlag New York, LLC. pp. 1–3, 191. ISBN 978-0-387-09539-4.
- ^ Shelby, RA; Smith, DR; Schultz, S (2001). "Experimental Verification of a Negative Index of Refraction". Science. 292 (5514): 77–9. Bibcode:2001Sci...292...77S. CiteSeerX 10.1.1.119.1617. doi:10.1126/science.1058847. PMID 11292865. S2CID 9321456.
- Sourkouhi, Zahra Sarpanah; Balasubramanian, Vishal; Zarifi, Mohammad Hossein (2024). "Optically Modulated Split Ring Resonator Sensor for Optical Density Analysis of Liquid Analytes in Microwave Regime". IEEE Transactions on Microwave Theory and Techniques: 1–9. doi:10.1109/TMTT.2024.3461568. ISSN 0018-9480.
- Yen, T. J.; et al. (2004). "Terahertz Magnetic Response from Artificial Materials". Science. 303 (5663): 1494–1496. Bibcode:2004Sci...303.1494Y. doi:10.1126/science.1094025. PMID 15001772. S2CID 14262927.
- ^ Kamil, Boratay Alici; Ekmel Özbay (2007-03-22). "Radiation properties of a split ring resonator and monopole composite" (PDF). Physica Status Solidi B. 244 (4): 1192–1196. Bibcode:2007PSSBR.244.1192A. doi:10.1002/pssb.200674505. hdl:11693/49278. S2CID 5348103. Retrieved 2009-09-17.
- ^ Movchan, A. B.; S. Guenneau (2004). "Split-ring resonators and localized modes" (PDF). Phys. Rev. B. 70 (12): 125116. Bibcode:2004PhRvB..70l5116M. doi:10.1103/PhysRevB.70.125116. Archived from the original (PDF) on 2016-02-22. Retrieved 2009-08-27.
- ^ Katsarakis, N.; T. Koschny; M. Kafesaki; E. N. Economou; C. M. Soukoulis (2004). "Electric coupling to the magnetic resonance of split ring resonators" (PDF). Appl. Phys. Lett. 84 (15): 2943–2945. arXiv:cond-mat/0407369. Bibcode:2004ApPhL..84.2943K. doi:10.1063/1.1695439. S2CID 27509585. Retrieved 2009-09-15.
- Smith, D. R.; J. J. Mock; A. F. Starr; D. Schurig (17 March 2005). "A gradient index metamaterial". Phys. Rev. E. 71 (3): 036609. arXiv:physics/0407063. Bibcode:2005PhRvE..71c6609S. doi:10.1103/PhysRevE.71.036609. PMID 15903607. S2CID 6121436.
- ^ Wu, B.-I.; W. Wang; J. Pacheco; X. Chen; T. Grzegorczyk; J. A. Kong (2005). "A Study of Using Metamaterials as Antenna Substrate to Enhance Gain". Progress in Electromagnetics Research. 51: 295–328. doi:10.2528/PIER04070701.
- ^ Slyusar V.I. Metamaterials on antenna solutions.// 7th International Conference on Antenna Theory and Techniques ICATT’09, Lviv, Ukraine, October 6–9, 2009. - Pp. 19 - 24
- J. Lezec, Henri; Jennifer A. Dionne; Harry A. Atwater (2007-04-20). "Negative Refraction at Visible Frequencies" (PDF). Science. 316 (5823): 430–2. Bibcode:2007Sci...316..430L. CiteSeerX 10.1.1.422.9475. doi:10.1126/science.1139266. PMID 17379773. S2CID 35189301. Retrieved 2009-10-06.
- ^ Smith DR, et al. (2000-05-01). "Composite Medium with Simultaneously Negative Permeability and Permittivity". Physical Review Letters. 84 (18): 4184–7. Bibcode:2000PhRvL..84.4184S. doi:10.1103/PhysRevLett.84.4184. PMID 10990641.
- Aydin, Koray; Irfan Bulu; Kaan Guven; Maria Kafesaki; Costas M Soukoulis; Ekmel Ozbay (2005-08-08). "Investigation of magnetic resonances for different SRR parameters and designs". New Journal of Physics. 7 (168): 168. Bibcode:2005NJPh....7..168A. doi:10.1088/1367-2630/7/1/168. hdl:11693/24008.
- Prati, Prati (2004-02-20). "Crossover Between the Cell Size and the Wavelength of the Incident Radiation in a Metamaterial" (PDF). Microwave and Optical Technology Letters. 40 (4): 269–272. doi:10.1002/mop.11349. S2CID 110004449. Archived from the original (PDF) on 2011-07-23.
- Wang, Bingnan; Jiangfeng Zhou; Thomas Koschny; Costas M. Soukoulis (2008-09-24). "Nonlinear properties of split-ring resonators" (PDF). Optics Express. 16 (20): 16058–. arXiv:0809.4045. Bibcode:2008OExpr..1616058W. doi:10.1364/OE.16.016058. PMID 18825245. S2CID 9428274. Archived from the original (PDF) on 2010-05-27. Retrieved 2009-10-25.
- Casse BD, et al. (2007). Towards 3D Electromagnetic Metamaterials in the THz Range (PDF). Synchronotron Radiation Instrumentation Ninth International Conference. Vol. 879. pp. 1462–1465. Bibcode:2007AIPC..879.1462C. doi:10.1063/1.2436340. Archived from the original (PDF) on March 12, 2020. Retrieved 2009-12-04.
- Dolling, G.; et al. (2005-12-01). "Cut-wire pairs and plate pairs as magnetic atoms for optical metamaterials" (PDF). Optics Letters. 30 (23): 3198–3200. arXiv:physics/0507045. Bibcode:2005OptL...30.3198D. doi:10.1364/OL.30.003198. PMID 16342719. S2CID 7537807. Archived from the original (Free PDf download) on 2010-04-15. Retrieved 2009-10-31.
- Paul, Oliver; et al. (2008-04-28). "Negative index bulk metamaterial at terahertz frequencies" (Free PDF download). Optics Express. 16 (9): 6736–44. Bibcode:2008OExpr..16.6736P. doi:10.1364/OE.16.006736. PMID 18545376. Retrieved 2009-11-01.
- Pendry, J., "New electromagnetic materials emphasize the negative, Archived 2011-07-17 at the Wayback Machine" Physics World, 1–5, 2001
- Wiltshire, M. C. K.; Hajnal, J; Pendry, J; Edwards, D; Stevens, C (2003-04-07). "Metamaterial endoscope for magnetic field transfer: near field imaging with magnetic wires". Opt Express. 11 (7): 709–15. Bibcode:2003OExpr..11..709W. doi:10.1364/OE.11.000709. PMID 19461782.
- Yuan, Hsiao-Kuan; et al. (2007-02-05). "A negative permeability material at red light". Optics Express. 15 (3): 1076–83. arXiv:physics/0610118. Bibcode:2007OExpr..15.1076Y. doi:10.1364/OE.15.001076. PMID 19532335. S2CID 5928393.
- Cai, Wenshan; Chettiar, UK; Yuan, HK; De Silva, VC; Kildishev, AV; Drachev, VP; Shalaev, VM (2007). "Metamagnetics with rainbow colors". Optics Express. 15 (6): 3333–3341. Bibcode:2007OExpr..15.3333C. doi:10.1364/OE.15.003333. PMID 19532574. Retrieved 2009-10-21.
- Enkrich, C.; et al. (2005). "Magnetic Metamaterials at Telecommunication and Visible Frequencies". Phys. Rev. Lett. 95 (20): 203901. arXiv:cond-mat/0504774. Bibcode:2005PhRvL..95t3901E. doi:10.1103/PhysRevLett.95.203901. PMID 16384056. S2CID 2975455.
Further reading
- Ates, Damla; Cakmak, Atilla Ozgur; Colak, Evrim; Zhao, Rongkuo; Soukoulis, C. M.; Ozbay, Ekmel (2010). "Transmission enhancement through deep subwavelength apertures using connected split ring resonators" (Free PDF download). Optics Express. 18 (4): 3952–66. Bibcode:2010OExpr..18.3952A. doi:10.1364/OE.18.003952. hdl:11693/13284. PMID 20389408.
- Shepard, K. W. et al. Split-ring resonator for the Argonne Superconducting Heavy Ion Booster. IEEE Transactions on Nuclear Science, VoL. NS-24, N0.3, JUN 1977.
External links
- Video: John Pendry lecture: The science of invisibility April 2009, SlowTV
- Split Ring Resonator Calculator: Online tool to calculate the LC equivalent circuit and resonant frequency of SRR and CSRR topologies.
 field parallel to the cylinders, the effective permeability can be written as the following. (This model is very limited and the effective permeability cannot be less than zero or greater than one.)
field parallel to the cylinders, the effective permeability can be written as the following. (This model is very limited and the effective permeability cannot be less than zero or greater than one.)

 is the resistance of the cylinder surface per unit area, a is the spacing of the cylinders,
is the resistance of the cylinder surface per unit area, a is the spacing of the cylinders,  is the angular frequency,
is the angular frequency,  is the permeability of free space and r is the radius. Moreover, when gaps are introduced to a double cylinder design similar to the image above, we see that the gaps produce a capacitance. This capacitor and inductor microstructure design introduces a resonance that amplifies the magnetic effect. The new form of the effective permeability resembles a familiar response known in plasmonic materials.
is the permeability of free space and r is the radius. Moreover, when gaps are introduced to a double cylinder design similar to the image above, we see that the gaps produce a capacitance. This capacitor and inductor microstructure design introduces a resonance that amplifies the magnetic effect. The new form of the effective permeability resembles a familiar response known in plasmonic materials.

