Misplaced Pages

In combinatorics, a square-free word is a word (a sequence of symbols) that does not contain any squares. A square is a word of the form XX, where X is not empty. Thus, a square-free word can also be defined as a word that avoids the pattern XX.

Finite square-free words

Binary alphabet

Over a binary alphabet ${\displaystyle \{0,1\}}$, the only square-free words are the empty word ${\displaystyle \epsilon ,0,1,01,10,010}$, and ${\displaystyle 101}$.

Ternary alphabet

Over a ternary alphabet ${\displaystyle \{0,1,2\}}$, there are infinitely many square-free words. It is possible to count the number ${\displaystyle c(n)}$ of ternary square-free words of length n.

The number of ternary square-free words of length n

n	0	1	2	3	4	5	6	7	8	9	10	11	12
⁠${\displaystyle c(n)}$⁠	1	3	6	12	18	30	42	60	78	108	144	204	264

This number is bounded by ${\displaystyle c(n)=\Theta (\alpha ^{n})}$, where ${\textstyle 1.3017597<\alpha <1.3017619}$. The upper bound on ${\displaystyle \alpha }$ can be found via Fekete's Lemma and approximation by automata. The lower bound can be found by finding a substitution that preserves square-freeness.

Alphabet with more than three letters

Since there are infinitely many square-free words over three-letter alphabets, this implies there are also infinitely many square-free words over an alphabet with more than three letters.

The following table shows the exact growth rate of the k-ary square-free words, rounded off to 7 digits after the decimal point, for k in the range from 4 to 15:

2-dimensional words

Consider a map ${\displaystyle {\textbf {w}}}$ from ${\displaystyle \mathbb {N} ^{2}}$ to A, where A is an alphabet and ${\displaystyle {\textbf {w}}}$ is called a 2-dimensional word. Let ${\displaystyle w_{m,n}}$ be the entry ${\displaystyle {\textbf {w}}(m,n)}$. A word ${\displaystyle {\textbf {x}}}$ is a line of ${\displaystyle {\textbf {w}}}$ if there exists ${\displaystyle i_{1},i_{2},j_{1},j_{2}}$such that ${\displaystyle {\text{gcd}}(j_{1},j_{2})=1}$, and for ${\displaystyle t\geq 0,x_{t}=w_{{i_{1}}+{j_{1}t},{i_{2}}+{j_{2}t}}}$.

Carpi proves that there exists a 2-dimensional word ${\displaystyle {\textbf {w}}}$ over a 16-letter alphabet such that every line of ${\displaystyle {\textbf {w}}}$ is square-free. A computer search shows that there are no 2-dimensional words ${\displaystyle {\textbf {w}}}$over a 7-letter alphabet, such that every line of ${\displaystyle {\textbf {w}}}$ is square-free.

Generating finite square-free words

Shur proposes an algorithm called R2F (random-t(w)o-free) that can generate a square-free word of length n over any alphabet with three or more letters. This algorithm is based on a modification of entropy compression: it randomly selects letters from a k-letter alphabet to generate a ⁠${\displaystyle (k+1)}$⁠-ary square-free word.

algorithm R2F is
    input: alphabet size ${\displaystyle k\geq 2}$,
           word length ${\displaystyle n>1}$
    output: a ⁠${\displaystyle (k+1)}$⁠-ary square-free word wof length n.
    (Note that ${\textstyle \color {gray}\Sigma _{k+1}}$ is the alphabet with letters ${\displaystyle \color {gray}\{1,...,k+1\}}$.)
    (For a word ${\displaystyle \color {gray}w\in \Sigma _{k}}$, ${\displaystyle \color {gray}\chi _{w}}$ is the permutation of ${\displaystyle \color {gray}\Sigma _{k}}$ such that a precedes b in ${\displaystyle \color {gray}\chi _{w}}$ if the 
     right most position of a in w is to the right of the rightmost position of b in w.
     For example,  ${\displaystyle \color {gray}w=136263163\in \Sigma _{6}}$ has ${\displaystyle \color {gray}\chi _{w}=361245}$.)
    choose ${\displaystyle w}$ in ${\textstyle \Sigma _{k+1}}$ uniformly at random 
    set ${\displaystyle \chi _{w}}$ to ${\displaystyle w}$ followed by all other letters of ${\textstyle \Sigma _{k+1}}$ in increasing order
    set the number N of iterations to 0
    while ${\displaystyle |w|<n}$ do
        choose j in ${\textstyle \Sigma _{k}}$ uniformly at random
        append ${\displaystyle a=\chi _{w}}$ to the end of w
        update ${\displaystyle \chi _{w}}$ shifting the first j elements to the right and setting ${\displaystyle \chi _{w}=a}$
        increment N by 1
        if w ends with a square of rank r then
            delete the last r letters of w
    return w

Every (k+1)-ary square-free word can be the output of Algorithm R2F, because on each iteration it can append any letter except for the last letter of w.

The expected number of random k-ary letters used by Algorithm R2F to construct a ⁠${\displaystyle (k+1)}$⁠-ary square-free word of length n is$${\displaystyle N=n\left(1+{\frac {2}{k^{2}}}+{\frac {1}{k^{3}}}+{\frac {4}{k^{4}}}+O\left({\frac {1}{k^{5}}}\right)\right)+O(1).}$$Note that there exists an algorithm that can verify the square-freeness of a word of length n in ${\displaystyle O(n\log n)}$ time. Apostolico and Preparata give an algorithm using suffix trees. Crochemore uses partitioning in his algorithm. Main and Lorentz provide an algorithm based on the divide-and-conquer method. A naive implementation may require ${\displaystyle O(n^{2})}$ time to verify the square-freeness of a word of length n.

Infinite square-free words

There exist infinitely long square-free words in any alphabet with three or more letters, as proved by Axel Thue.

Examples

First difference of the Thue–Morse sequence

One example of an infinite square-free word over an alphabet of size 3 is the word over the alphabet ${\displaystyle \{-1,0,+1\}}$ obtained by taking the first difference of the Thue–Morse sequence. That is, from the Thue–Morse sequence

${\displaystyle 0,1,1,0,1,0,0,1,1,0,0,1,0,1,1,0...}$

one forms a new sequence in which each term is the difference of two consecutive terms of the Thue–Morse sequence. The resulting square-free word is

${\displaystyle 1,0,-1,1,-1,0,1,0,-1,0,1,-1,1,0,-1,...}$(sequence A029883 in the OEIS).

Leech's morphism

Another example found by John Leech is defined recursively over the alphabet ${\displaystyle \{0,1,2\}}$. Let ⁠${\displaystyle w_{1}}$⁠ be any square-free word starting with the letter 0. Define the words ${\displaystyle \{w_{i}\mid i\in \mathbb {N} \}}$ recursively as follows: the word ${\displaystyle w_{i+1}}$ is obtained from ⁠${\displaystyle w_{i}}$⁠ by replacing each 0 in ⁠${\displaystyle w_{i}}$⁠ with 0121021201210, each 1 with 1202102012021, and each 2 with 2010210120102. It is possible to prove that the sequence converges to the infinite square-free word

0121021201210120210201202120102101201021202102012021...

Generating infinite square-free words

Infinite square-free words can be generated by square-free morphism. A morphism is called square-free if the image of every square-free word is square-free. A morphism is called k–square-free if the image of every square-free word of length k is square-free.

Crochemore proves that a uniform morphism h is square-free if and only if it is 3-square-free. In other words, h is square-free if and only if ${\displaystyle h(w)}$ is square-free for all square-free w of length 3. It is possible to find a square-free morphism by brute-force search.

algorithm square-free_morphism is
    output: a square-free morphism with the lowest possible rank k.
    set ${\displaystyle k=3}$
    while True do
        set k_sf_words to the list of all square-free words of length k over a ternary alphabet
        for each ${\displaystyle h(0)}$ in k_sf_words do
            for each ${\displaystyle h(1)}$ in k_sf_words do
                for each ${\displaystyle h(2)}$ in k_sf_words do
                    if ${\displaystyle h(1)=h(2)}$ then
                        break from the current loop (advance to next ${\displaystyle h(1)}$)
                    if ${\displaystyle h(0)\neq h(1)}$ and ${\displaystyle h(2)\neq h(0)}$ then
                        if ${\displaystyle h(w)}$ is square-free for all square-free w of length 3 then
                            return ${\displaystyle h(0),h(1),h(2)}$
        increment k by 1

Over a ternary alphabet, there are exactly 144 uniform square-free morphisms of rank 11 and no uniform square-free morphisms with a lower rank than 11.

To obtain an infinite square-free words, start with any square-free word such as 0, and successively apply a square-free morphism h to it. The resulting words preserve the property of square-freeness. For example, let h be a square-free morphism, then as ${\displaystyle w\to \infty }$, ${\displaystyle h^{w}(0)}$ is an infinite square-free word.

Note that, if a morphism over a ternary alphabet is not uniform, then this morphism is square-free if and only if it is 5-square-free.

Letter combinations in square-free words

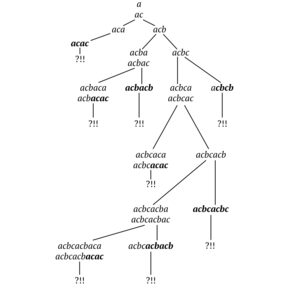
Avoid two-letter combinations

Over a ternary alphabet, a square-free word of length more than 13 contains all the square-free two-letter combinations.

This can be proved by constructing a square-free word without the two-letter combination ab. As a result, bcbacbcacbaca is the longest square-free word without the combination ab and its length is equal to 13.

Note that over a more than three-letter alphabet there are square-free words of any length without an arbitrary two-letter combination.

Avoid three-letter combinations

Over a ternary alphabet, a square-free word of length more than 36 contains all the square-free three-letter combinations.

However, there are square-free words of any length without the three-letter combination aba.

Note that over a more than three-letter alphabet there are square-free words of any length without an arbitrary three-letter combination.

Density of a letter

The density of a letter a in a finite word w is defined as ${\displaystyle {\frac {|w|_{a}}{|w|}}}$ where ${\displaystyle |w|_{a}}$ is the number of occurrences of a in ${\displaystyle w}$ and ${\displaystyle |w|}$ is the length of the word. The density of a letter a in an infinite word is ${\displaystyle \liminf _{l\to \infty }{\frac {|w_{l}|_{a}}{|w_{l}|}}}$ where ${\displaystyle w_{l}}$ is the prefix of the word w of length l.

The minimal density of a letter a in an infinite ternary square-free word is equal to ${\displaystyle {\frac {883}{3215}}\approx 0.2747}$.

The maximum density of a letter a in an infinite ternary square-free word is equal to ${\displaystyle {\frac {255}{653}}\approx 0.3905}$.

Notes

1. "A006156 - OEIS". oeis.org. Retrieved 2019-03-28.
2. ^ Shur, Arseny (2011). "Growth properties of power-free languages". Computer Science Review. 6 (5–6): 28–43. doi:10.1016/j.cosrev.2012.09.001.
3. Berthe, Valerie; Rigo, Michel, eds. (2016). "Preface". Combinatorics, Words and Symbolic Dynamics. Cambridge University Press. pp. xi–xviii. doi:10.1017/cbo9781139924733.001. ISBN 9781139924733.
4. Carpi, Arturo (1988). "Multidimensional unrepetitive configurations". Theoretical Computer Science. 56 (2): 233–241. doi:10.1016/0304-3975(88)90080-1. ISSN 0304-3975.
5. Shur, Arseny (2015). "Generating square-free words efficiently". Theoretical Computer Science. 601: 67–72. doi:10.1016/j.tcs.2015.07.027. hdl:10995/92700.
6. Apostolico, A.; Preparata, F.P. (Feb 1983). "Optimal off-line detection of repetitions in a string". Theoretical Computer Science. 22 (3): 297–315. doi:10.1016/0304-3975(83)90109-3. ISSN 0304-3975.
7. Crochemore, Max (Oct 1981). "An optimal algorithm for computing the repetitions in a word". Information Processing Letters. 12 (5): 244–250. doi:10.1016/0020-0190(81)90024-7. ISSN 0020-0190.
8. Main, Michael G; Lorentz, Richard J (Sep 1984). "An O(n log n) algorithm for finding all repetitions in a string". Journal of Algorithms. 5 (3): 422–432. doi:10.1016/0196-6774(84)90021-x. ISSN 0196-6774.
9. ^ Berstel, Jean (1994). Axel Thue's papers on repetitions in words a translation. Départements de mathématiques et d'informatique, Université du Québec à Montréal. ISBN 978-2892761405. OCLC 494791187.
10. Leech, J. (1957). "A problem on strings of beads". Math. Gaz. 41: 277–278. doi:10.1017/S0025557200236115. S2CID 126406225. Zbl 0079.01101.
11. ^ Berstel, Jean (April 1984). "Some Recent Results on Squarefree Words". Annual Symposium on Theoretical Aspects of Computer Science. Lecture Notes in Computer Science. Vol. 166. pp. 14–25. doi:10.1007/3-540-12920-0_2. ISBN 978-3-540-12920-2.
12. ^ Zolotov, Boris (2015). "Another Solution to the Thue Problem of Non-Repeating Words". arXiv:1505.00019 .
13. ^ Khalyavin, Andrey (2007). "The minimal density of a letter in an infinite ternary square-free word is 883/3215" (PDF). Journal of Integer Sequences. 10 (2): 3. Bibcode:2007JIntS..10...65K.
14. Ochem, Pascal (2007). "Letter frequency in infinite repetition-free words". Theoretical Computer Science. 380 (3): 388–392. doi:10.1016/j.tcs.2007.03.027. ISSN 0304-3975.

References

• Berstel, Jean; Lauve, Aaron; Reutenauer, Christophe; Saliola, Franco V. (2009). Combinatorics on words. Christoffel words and repetitions in words. CRM Monograph Series. Vol. 27. Providence, RI: American Mathematical Society. ISBN 978-0-8218-4480-9. Zbl 1161.68043.
• Lothaire, M. (1997). Combinatorics on words. Cambridge: Cambridge University Press. ISBN 978-0-521-59924-5..
• Lothaire, M. (2011). Algebraic combinatorics on words. Encyclopedia of Mathematics and Its Applications. Vol. 90. With preface by Jean Berstel and Dominique Perrin (Reprint of the 2002 hardback ed.). Cambridge University Press. ISBN 978-0-521-18071-9. Zbl 1221.68183.
• Pytheas Fogg, N. (2002). Berthé, Valérie; Ferenczi, Sébastien; Mauduit, Christian; Siegel, Anne (eds.). Substitutions in dynamics, arithmetics and combinatorics. Lecture Notes in Mathematics. Vol. 1794. Berlin: Springer-Verlag. ISBN 978-3-540-44141-0. Zbl 1014.11015.

• Formal languages
• Combinatorics on words