Misplaced Pages

Action principles lie at the heart of fundamental physics, from classical mechanics through quantum mechanics, particle physics, and general relativity. Action principles start with an energy function called a Lagrangian describing the physical system. The accumulated value of this energy function between two states of the system is called the action. Action principles apply the calculus of variation to the action. The action depends on the energy function, and the energy function depends on the position, motion, and interactions in the system: variation of the action allows the derivation of the equations of motion without vector or forces.

Several distinct action principles differ in the constraints on their initial and final conditions. The names of action principles have evolved over time and differ in details of the endpoints of the paths and the nature of the variation. Quantum action principles generalize and justify the older classical principles. Action principles are the basis for Feynman's version of quantum mechanics, general relativity and quantum field theory.

The action principles have applications as broad as physics, including many problems in classical mechanics but especially in modern problems of quantum mechanics and general relativity. These applications built up over two centuries as the power of the method and its further mathematical development rose.

This article introduces the action principle concepts and summarizes other articles with more details on concepts and specific principles.

Common concepts

Action principles are "integral" approaches rather than the "differential" approach of Newtonian mechanics. The core ideas are based on energy, paths, an energy function called the Lagrangian along paths, and selection of a path according to the "action", a continuous sum or integral of the Lagrangian along the path.

Energy, not force

Introductory study of mechanics, the science of interacting objects, typically begins with Newton's laws based on the concept of force, defined by the acceleration it causes when applied to mass: ${\displaystyle F=ma.}$ This approach to mechanics focuses on a single point in space and time, attempting to answer the question: "What happens next?". Mechanics based on action principles begin with the concept of action, an energy tradeoff between kinetic energy and potential energy, defined by the physics of the problem. These approaches answer questions relating starting and ending points: Which trajectory will place a basketball in the hoop? If we launch a rocket to the Moon today, how can it land there in 5 days? The Newtonian and action-principle forms are equivalent, and either one can solve the same problems, but selecting the appropriate form will make solutions much easier.

The energy function in the action principles is not the total energy (conserved in an isolated system), but the Lagrangian, the difference between kinetic and potential energy. The kinetic energy combines the energy of motion for all the objects in the system; the potential energy depends upon the instantaneous position of the objects and drives the motion of the objects. The motion of the objects places them in new positions with new potential energy values, giving a new value for the Lagrangian.

Using energy rather than force gives immediate advantages as a basis for mechanics. Force mechanics involves 3-dimensional vector calculus, with 3 space and 3 momentum coordinates for each object in the scenario; energy is a scalar magnitude combining information from all objects, giving an immediate simplification in many cases. The components of force vary with coordinate systems; the energy value is the same in all coordinate systems. Force requires an inertial frame of reference; once velocities approach the speed of light, special relativity profoundly affects mechanics based on forces. In action principles, relativity merely requires a different Lagrangian: the principle itself is independent of coordinate systems.

Paths, not points

The explanatory diagrams in force-based mechanics usually focus on a single point, like the center of momentum, and show vectors of forces and velocities. The explanatory diagrams of action-based mechanics have two points with actual and possible paths connecting them. These diagrammatic conventions reiterate the different strong points of each method.

Depending on the action principle, the two points connected by paths in a diagram may represent two particle positions at different times, or the two points may represent values in a configuration space or in a phase space. The mathematical technology and terminology of action principles can be learned by thinking in terms of physical space, then applied in the more powerful and general abstract spaces.

Action along a path

Action principles assign a number—the action—to each possible path between two points. This number is computed by adding an energy value for each small section of the path multiplied by the time spent in that section:

action ${\displaystyle S=\int _{t_{1}}^{t_{2}}{\big (}{\text{KE}}(t)-{\text{PE}}(t){\big )}\,dt,}$

where the form of the kinetic (${\displaystyle {\text{KE}}}$) and potential (${\displaystyle {\text{PE}}}$) energy expressions depend upon the physics problem, and their value at each point on the path depends upon relative coordinates corresponding to that point. The energy function is called a Lagrangian; in simple problems it is the kinetic energy minus the potential energy of the system.

Path variation

A system moving between two points takes one particular path; other similar paths are not taken. Each path corresponds to a value of the action. An action principle predicts or explains that the particular path taken has a stationary value for the system's action: similar paths near the one taken have very similar action value. This variation in the action value is key to the action principles.

The symbol ${\displaystyle \delta }$ is used to indicate the path variations so an action principle appears mathematically as

${\displaystyle (\delta S)_{C}=0,}$

meaning that at the stationary point, the variation of the action ${\displaystyle S}$ with some fixed constraints ${\displaystyle C}$ is zero. For action principles, the stationary point may be a minimum or a saddle point, but not a maximum. Elliptical planetary orbits provide a simple example of two paths with equal action – one in each direction around the orbit; neither can be the minimum or "least action". The path variation implied by ${\displaystyle \delta }$ is not the same as a differential like ${\displaystyle dt}$. The action integral depends on the coordinates of the objects, and these coordinates depend upon the path taken. Thus the action integral is a functional, a function of a function.

Conservation principles

An important result from geometry known as Noether's theorem states that any conserved quantities in a Lagrangian imply a continuous symmetry and conversely. For examples, a Lagrangian independent of time corresponds to a system with conserved energy; spatial translation independence implies momentum conservation; angular rotation invariance implies angular momentum conservation. These examples are global symmetries, where the independence is itself independent of space or time; more general local symmetries having a functional dependence on space or time lead to gauge theory. The observed conservation of isospin was used by Yang Chen-Ning and Robert Mills in 1953 to construct a gauge theory for mesons, leading some decades later to modern particle physics theory.

Distinct principles

Action principles apply to a wide variety of physical problems, including all of fundamental physics. The only major exceptions are cases involving friction or when only the initial position and velocities are given. Different action principles have different meaning for the variations; each specific application of an action principle requires a specific Lagrangian describing the physics. A common name for any or all of these principles is "the principle of least action". For a discussion of the names and historical origin of these principles see action principle names.

Fixed endpoints with conserved energy

When total energy and the endpoints are fixed, Maupertuis's least action principle applies. For example, to score points in basketball the ball must leave the shooters hand and go through the hoop, but the time of the flight is not constrained. Maupertuis's least action principle is written mathematically as the stationary condition $${\displaystyle (\delta W)_{E}=0}$$ on the abbreviated action $${\displaystyle W\ {\stackrel {\text{def}}{=}}\ \int _{q_{1}}^{q_{2}}\mathbf {p} \cdot \mathbf {dq} ,}$$ (sometimes written ${\displaystyle S_{0}}$), where ${\displaystyle \mathbf {p} =(p_{1},p_{2},\ldots ,p_{N})}$ are the particle momenta or the conjugate momenta of generalized coordinates, defined by the equation $${\displaystyle p_{k}\ {\stackrel {\text{def}}{=}}\ {\frac {\partial L}{\partial {\dot {q}}_{k}}},}$$ where ${\displaystyle L(\mathbf {q} ,{\dot {\mathbf {q} }},t)}$ is the Lagrangian. Some textbooks write ${\displaystyle (\delta W)_{E}=0}$ as ${\displaystyle \Delta S_{0}}$, to emphasize that the variation used in this form of the action principle differs from Hamilton's variation. Here the total energy ${\displaystyle E}$ is fixed during the variation, but not the time, the reverse of the constraints on Hamilton's principle. Consequently, the same path and end points take different times and energies in the two forms. The solutions in the case of this form of Maupertuis's principle are orbits: functions relating coordinates to each other in which time is simply an index or a parameter.

Time-independent potentials; no forces

For time-invariant system, the action ${\displaystyle S}$ relates simply to the abbreviated action ${\displaystyle W}$ on the stationary path as $${\displaystyle \Delta S=\Delta W-E\Delta t}$$ for energy ${\displaystyle E}$ and time difference ${\displaystyle \Delta t=t_{2}-t_{1}}$. For a rigid body with no net force, the actions are identical, and the variational principles become equivalent to Fermat's principle of least time: $${\displaystyle \delta (t_{2}-t_{1})=0.}$$

Fixed events

When the physics problem gives the two endpoints as a position and a time, that is as events, Hamilton's action principle applies. For example, imagine planning a trip to the Moon. During your voyage the Moon will continue its orbit around the Earth: it's a moving target. Hamilton's principle for objects at positions ${\displaystyle \mathbf {q} (t)}$ is written mathematically as $${\displaystyle (\delta {\mathcal {S}})_{\Delta t}=0,\ \mathrm {where} \ {\mathcal {S}}\ {\stackrel {\mathrm {def} }{=}}\ \int _{t_{1}}^{t_{2}}L(\mathbf {q} (t),{\dot {\mathbf {q} }}(t),t)\,dt.}$$ The constraint ${\displaystyle \Delta t=t_{2}-t_{1}}$ means that we only consider paths taking the same time, as well as connecting the same two points ${\displaystyle \mathbf {q} (t_{1})}$ and ${\displaystyle \mathbf {q} (t_{2})}$. The Lagrangian ${\displaystyle L=T-V}$ is the difference between kinetic energy and potential energy at each point on the path. Solution of the resulting equations gives the world line ${\displaystyle \mathbf {q} (t)}$. Starting with Hamilton's principle, the local differential Euler–Lagrange equation can be derived for systems of fixed energy. The action ${\displaystyle S}$ in Hamilton's principle is the Legendre transformation of the action in Maupertuis' principle.

Classical field theory

The concepts and many of the methods useful for particle mechanics also apply to continuous fields. The action integral runs over a Lagrangian density, but the concepts are so close that the density is often simply called the Lagrangian.

Quantum action principles

For quantum mechanics, the action principles have significant advantages: only one mechanical postulate is needed, if a covariant Lagrangian is used in the action, the result is relativistically correct, and they transition clearly to classical equivalents.

Both Richard Feynman and Julian Schwinger developed quantum action principles based on early work by Paul Dirac. Feynman's integral method was not a variational principle but reduces to the classical least action principle; it led to his Feynman diagrams. Schwinger's differential approach relates infinitesimal amplitude changes to infinitesimal action changes.

Feynman's action principle

When quantum effects are important, new action principles are needed. Instead of a particle following a path, quantum mechanics defines a probability amplitude ${\displaystyle \psi (x_{k},t)}$ at one point ${\displaystyle x_{k}}$ and time ${\displaystyle t}$ related to a probability amplitude at a different point later in time: $${\displaystyle \psi (x_{k+1},t+\varepsilon )={\frac {1}{A}}\int e^{iS(x_{k+1},x_{k})/\hbar }\psi (x_{k},t)\,dx_{k},}$$ where ${\displaystyle S(x_{k+1},x_{k})}$ is the classical action. Instead of single path with stationary action, all possible paths add (the integral over ${\displaystyle x_{k}}$), weighted by a complex probability amplitude ${\displaystyle e^{iS/\hbar }}$. The phase of the amplitude is given by the action divided by the Planck constant or quantum of action: ${\displaystyle S/\hbar }$. When the action of a particle is much larger than ${\displaystyle \hbar }$, ${\displaystyle S/\hbar \gg 1}$, the phase changes rapidly along the path: the amplitude averages to a small number. Thus the Planck constant sets the boundary between classical and quantum mechanics.

All of the paths contribute in the quantum action principle. At the end point, where the paths meet, the paths with similar phases add, and those with phases differing by ${\displaystyle \pi }$ subtract. Close to the path expected from classical physics, phases tend to align; the tendency is stronger for more massive objects that have larger values of action. In the classical limit, one path dominates – the path of stationary action.

Schwinger's action principle

Schwinger's approach relates variations in the transition amplitudes ${\displaystyle (q_{\text{f}}|q_{\text{i}})}$ to variations in an action matrix element:

${\displaystyle \delta (q_{r_{\text{f}}}|q_{r_{\text{i}}})=i(q_{r_{\text{f}}}|\delta S|q_{r_{\text{i}}}),}$

where the action operator is

${\displaystyle S=\int _{t_{\text{i}}}^{t_{\text{f}}}L\,dt.}$

The Schwinger form makes analysis of variation of the Lagrangian itself, for example, variation in potential source strength, especially transparent.

The optico-mechanical analogy

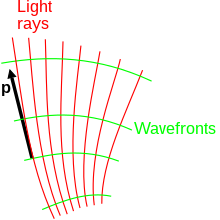
For every path, the action integral builds in value from zero at the starting point to its final value at the end. Any nearby path has similar values at similar distances from the starting point. Lines or surfaces of constant partial action value can be drawn across the paths, creating a wave-like view of the action. Analysis like this connects particle-like rays of geometrical optics with the wavefronts of Huygens–Fresnel principle.

... thus pointed to that remarkable analogy between optical and mechanical phenomena which was observed much earlier by John Bernoulli and which was later fully developed in Hamilton's ingenious optico-mechanical theory. This analogy played a fundamental role in the development of modern wave-mechanics.

— C. Lanczos

Applications

Action principles are applied to derive differential equations like the Euler–Lagrange equations or as direct applications to physical problems.

Classical mechanics

Action principles can be directly applied to many problems in classical mechanics, e.g. the shape of elastic rods under load, the shape of a liquid between two vertical plates (a capillary), or the motion of a pendulum when its support is in motion.

Chemistry

Quantum action principles are used in the quantum theory of atoms in molecules (QTAIM), a way of decomposing the computed electron density of molecules in to atoms as a way of gaining insight into chemical bonding.

General relativity

Inspired by Einstein's work on general relativity, the renowned mathematician David Hilbert applied the principle of least action to derive the field equations of general relativity. His action, now known as the Einstein–Hilbert action,

${\displaystyle S={\frac {1}{2\kappa }}\int R{\sqrt {-g}}\,\mathrm {d} ^{4}x,}$

contained a relativistically invariant volume element ${\displaystyle {\sqrt {-g}}\,\mathrm {d} ^{4}x}$ and the Ricci scalar curvature ${\displaystyle R}$. The scale factor ${\displaystyle \kappa }$ is the Einstein gravitational constant.

Other applications

The action principle is so central in modern physics and mathematics that it is widely applied including in thermodynamics, fluid mechanics, the theory of relativity, quantum mechanics, particle physics, and string theory.

History

The action principle is preceded by earlier ideas in optics. In ancient Greece, Euclid wrote in his Catoptrica that, for the path of light reflecting from a mirror, the angle of incidence equals the angle of reflection. Hero of Alexandria later showed that this path has the shortest length and least time.

Building on the early work of Pierre Louis Maupertuis, Leonhard Euler, and Joseph-Louis Lagrange defining versions of principle of least action, William Rowan Hamilton and in tandem Carl Gustav Jacob Jacobi developed a variational form for classical mechanics known as the Hamilton–Jacobi equation.

In 1915, David Hilbert applied the variational principle to derive Albert Einstein's equations of general relativity.

In 1933, the physicist Paul Dirac demonstrated how this principle can be used in quantum calculations by discerning the quantum mechanical underpinning of the principle in the quantum interference of amplitudes. Subsequently Julian Schwinger and Richard Feynman independently applied this principle in quantum electrodynamics.

References

1. Thomas A. Moore "Least-Action Principle" in Macmillan Encyclopedia of Physics, John Rigden, editor, Simon & Schuster Macmillan, 1996, volume 2, page 840.
2. ^ Yourgrau, Wolfgang; Mandelstam, Stanley (1979). Variational principles in dynamics and quantum theory. Dover books on physics and chemistry (Republ. of the 3rd ed., publ. in 1968 ed.). New York, NY: Dover Publ. ISBN 978-0-486-63773-0.
3. ^ Hanc, Jozef; Taylor, Edwin F.; Tuleja, Slavomir (2005-07-01). "Variational mechanics in one and two dimensions". American Journal of Physics. 73 (7): 603–610. Bibcode:2005AmJPh..73..603H. doi:10.1119/1.1848516. ISSN 0002-9505.
4. Coopersmith, Jennifer (2017). The lazy universe : an introduction to the principle of least action. Oxford; New York, NY : Oxford University Press. ISBN 978-0-19-874304-0.
5. ^ Lanczos, Cornelius (1986). The variational principles of mechanics (4 ed.). New York: Dover. ISBN 978-0-486-65067-8.
6. Kleppner, Daniel; Kolenkow, Robert J. (2014). "Chapter 3: Forces and equations of motion". An Introduction to Mechanics (2nd ed.). Cambridge: Cambridge University Press. ISBN 978-0521198110.
7. Moore, Thomas A. (2004-04-01). "Getting the most action out of least action: A proposal". American Journal of Physics. 72 (4): 522–527. Bibcode:2004AmJPh..72..522M. doi:10.1119/1.1646133. ISSN 0002-9505.
8. ^ "Ch. 19: The Principle of Least Action". The Feynman Lectures on Physics. Vol. II. Retrieved 2023-11-03.
9. ^ Goldstein, Herbert; Poole, Charles P.; Safko, John L. (2008). Classical mechanics (3rd ed.,  ed.). San Francisco, Munich: Addison Wesley. ISBN 978-0-201-65702-9.
10. Gray, C. G.; Taylor, Edwin F. (May 2007). "When action is not least". American Journal of Physics. 75 (5): 434–458. Bibcode:2007AmJPh..75..434G. doi:10.1119/1.2710480. ISSN 0002-9505.
11. Hill, E. L. (1951-07-01). "Hamilton's Principle and the Conservation Theorems of Mathematical Physics". Reviews of Modern Physics. 23 (3): 253–260. Bibcode:1951RvMP...23..253H. doi:10.1103/RevModPhys.23.253. ISSN 0034-6861.
12. Penrose, Roger (2005). The road to reality: a complete guide to the laws of the universe. New York: Alfred A. Knopf. ISBN 978-0-679-45443-4.
13. Brading, Katherine (March 2002). "Which Symmetry? Noether, Weyl, and Conservation of Electric Charge". Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics. 33 (1): 3–22. Bibcode:2002SHPMP..33....3B. doi:10.1016/S1355-2198(01)00033-8.
14. Baggott, J. E. (2013). The quantum story: a history in 40 moments (Impression: 3 ed.). Oxford: Oxford Univ. Press. ISBN 978-0-19-956684-6.
15. Hand, Louis N.; Finch, Janet D. (2008). Analytical mechanics (7. print ed.). Cambridge: Cambridge Univ. Press. ISBN 978-0-521-57572-0.
16. ^ Gray, Chris G. (2009-12-09). "Principle of least action". Scholarpedia. 4 (12): 8291. Bibcode:2009SchpJ...4.8291G. doi:10.4249/scholarpedia.8291.
17. Kibble, T. W. B.; Berkshire, F. H. (2004). Classical Mechanics (5th ed.). Imperial College Press. ISBN 9781860944352.
18. Gray, C. G.; Karl, G.; Novikov, V. A. (2004-02-01). "Progress in classical and quantum variational principles". Reports on Progress in Physics. 67 (2): 159–208. arXiv:physics/0312071. Bibcode:2004RPPh...67..159G. doi:10.1088/0034-4885/67/2/R02. ISSN 0034-4885.
19. Peskin, Michael E. (2018-01-31). An Introduction To Quantum Field Theory. Boca Raton: CRC Press. doi:10.1201/9780429503559. ISBN 978-0-429-50355-9.
20. Feynman, R. P. (1948-04-01). "Space-Time Approach to Non-Relativistic Quantum Mechanics". Reviews of Modern Physics. 20 (2): 367–387. Bibcode:1948RvMP...20..367F. doi:10.1103/RevModPhys.20.367. ISSN 0034-6861.
21. Curtis, Lorenzo J. (2011-09-01). "A 21st century perspective as a primer to introductory physics". European Journal of Physics. 32 (5): 1259–1274. Bibcode:2011EJPh...32.1259C. doi:10.1088/0143-0807/32/5/014. ISSN 0143-0807.
22. Ogborn, Jon; Taylor, Edwin F. (2004-12-24). "Quantum physics explains Newton's laws of motion" (PDF). Physics Education. 40 (1): 26–34. doi:10.1088/0031-9120/40/1/001. ISSN 0031-9120.
23. ^ Dittrich, Walter (2021). The Development of the Action Principle: A Didactic History from Euler-Lagrange to Schwinger. SpringerBriefs in Physics. Cham: Springer International Publishing. doi:10.1007/978-3-030-69105-9. ISBN 978-3-030-69104-2.
24. Bader, Richard F. W. (June 2005). "The Quantum Mechanical Basis of Conceptual Chemistry". Monatshefte für Chemie – Chemical Monthly. 136 (6): 819–854. doi:10.1007/s00706-005-0307-x. ISSN 0026-9247.
25. Rojo, Alberto; Bloch, Anthony, eds. (2018). "Relativity and Least Action". The Principle of Least Action: History and Physics. Cambridge: Cambridge University Press. pp. 162–188. doi:10.1017/9781139021029.007. ISBN 978-0-521-86902-7.
26. García-Morales, Vladimir; Pellicer, Julio; Manzanares, José A. (2008). "Thermodynamics based on the principle of least abbreviated action: Entropy production in a network of coupled oscillators". Annals of Physics. 323 (8): 1844–1858. arXiv:cond-mat/0602186. Bibcode:2008AnPhy.323.1844G. doi:10.1016/j.aop.2008.04.007. S2CID 118464686.
27. Gay-Balmaz, François; Yoshimura, Hiroaki (2018). "From Lagrangian Mechanics to Nonequilibrium Thermodynamics: A Variational Perspective". Entropy. 21 (1): 8. arXiv:1904.03738. Bibcode:2018Entrp..21....8G. doi:10.3390/e21010008. ISSN 1099-4300. PMC 7514189. PMID 33266724.
28. Biot, Maurice Anthony (1975). "A virtual dissipation principle and Lagrangian equations in non-linear irreversible thermodynamics". Bulletin de la Classe des sciences. 61 (1): 6–30. doi:10.3406/barb.1975.57878. ISSN 0001-4141.
29. Gray, Chris (2009). "Principle of least action". Scholarpedia. 4 (12): 8291. Bibcode:2009SchpJ...4.8291G. doi:10.4249/scholarpedia.8291.
30. Feynman, Richard Phillips (1942), The Principle of Least Action in Quantum Mechanics (thesis), Bibcode:1942PhDT.........5F.
31. "Principle of Least Action – damtp" (PDF). Archived from the original (PDF) on 2015-10-10. Retrieved 2016-07-18.
32. Helzberger, Max (1966). "Optics from Euclid to Huygens". Applied Optics. 5 (9): 1383–1893. Bibcode:1966ApOpt...5.1383H. doi:10.1364/AO.5.001383. PMID 20057555. In Catoptrics the law of reflection is stated, namely that incoming and outgoing rays form the same angle with the surface normal.
33. Kline, Morris (1972). Mathematical Thought from Ancient to Modern Times. New York: Oxford University Press. pp. 167–168. ISBN 0-19-501496-0.
34. Kline, Morris (1972). Mathematical Thought from Ancient to Modern Times. New York: Oxford University Press. pp. 167–168. ISBN 0-19-501496-0.
35. Nakane, Michiyo, and Craig G. Fraser. "The Early History of Hamilton-Jacobi Dynamics 1834–1837." Centaurus 44.3-4 (2002): 161–227.
36. Mehra, Jagdish (1987). "Einstein, Hilbert, and the Theory of Gravitation". In Mehra, Jagdish (ed.). The physicist's conception of nature (Reprint ed.). Dordrecht: Reidel. ISBN 978-90-277-2536-3.
37. Dirac, Paul A. M. (1933). "The Lagrangian in Quantum Mechanics" (PDF). Physikalische Zeitschrift der Sowjetunion. 3 (1): 64–72.
38. R. Feynman, Quantum Mechanics and Path Integrals, McGraw-Hill (1965), ISBN 0-07-020650-3.
39. J. S. Schwinger, Quantum Kinematics and Dynamics, W. A. Benjamin (1970), ISBN 0-7382-0303-3.

• Dynamics (mechanics)
• Classical mechanics