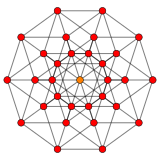
| Orthogonal projections in B5 Coxeter plane | ||
|---|---|---|
In five-dimensional geometry, a steric 5-cube or (steric 5-demicube or sterihalf 5-cube) is a convex uniform 5-polytope. There are unique 4 steric forms of the 5-cube. Steric 5-cubes have half the vertices of stericated 5-cubes.
Steric 5-cube
| Steric 5-cube | |
|---|---|
| Type | uniform polyteron |
| Schläfli symbol |
|
| Coxeter-Dynkin diagram | |
| 4-faces | 82 |
| Cells | 480 |
| Faces | 720 |
| Edges | 400 |
| Vertices | 80 |
| Vertex figure | {3,3}-t1{3,3} antiprism |
| Coxeter groups | D5, |
| Properties | convex |
Alternate names
- Steric penteract, runcinated demipenteract
- Small prismated hemipenteract (siphin) (Jonathan Bowers)
Cartesian coordinates
The Cartesian coordinates for the 80 vertices of a steric 5-cube centered at the origin are the permutations of
- (±1,±1,±1,±1,±3)
with an odd number of plus signs.
Images
| Coxeter plane | B5 | |
|---|---|---|
| Graph | 
| |
| Dihedral symmetry | ||
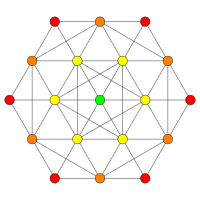
| Coxeter plane | D5 | D4 |
| Graph | 
|
|
| Dihedral symmetry | ||
| Coxeter plane | D3 | A3 |
| Graph | 
|

|
| Dihedral symmetry |
Related polytopes
| Dimensional family of steric n-cubes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| n | 5 | 6 | 7 | 8 | |||||||
= |
= |
= |
= |
= | |||||||
| Steric figure |

|
|
|

| |||||||
| Coxeter | = |
= |
= |
= | |||||||
| Schläfli | h4{4,3} | h4{4,3} | h4{4,3} | h4{4,3} | |||||||
Stericantic 5-cube
| Stericantic 5-cube | |
|---|---|
| Type | uniform polyteron |
| Schläfli symbol |
|
| Coxeter-Dynkin diagram | |
| 4-faces | 82 |
| Cells | 720 |
| Faces | 1840 |
| Edges | 1680 |
| Vertices | 480 |
| Vertex figure | |
| Coxeter groups | D5, |
| Properties | convex |
Alternate names
- Prismatotruncated hemipenteract (pithin) (Jonathan Bowers)
Cartesian coordinates
The Cartesian coordinates for the 480 vertices of a stericantic 5-cube centered at the origin are coordinate permutations:
- (±1,±1,±3,±3,±5)
with an odd number of plus signs.
Images
| Coxeter plane | B5 | |
|---|---|---|
| Graph | 
| |
| Dihedral symmetry | ||
| Coxeter plane | D5 | D4 |
| Graph | 
|

|
| Dihedral symmetry | ||
| Coxeter plane | D3 | A3 |
| Graph | 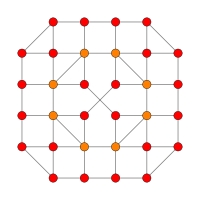
|
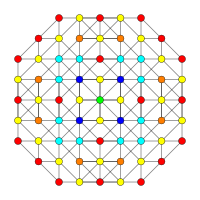
|
| Dihedral symmetry |
Steriruncic 5-cube
| Steriruncic 5-cube | |
|---|---|
| Type | uniform polyteron |
| Schläfli symbol |
|
| Coxeter-Dynkin diagram | |
| 4-faces | 82 |
| Cells | 560 |
| Faces | 1280 |
| Edges | 1120 |
| Vertices | 320 |
| Vertex figure | |
| Coxeter groups | D5, |
| Properties | convex |
Alternate names
- Prismatorhombated hemipenteract (pirhin) (Jonathan Bowers)
Cartesian coordinates
The Cartesian coordinates for the 320 vertices of a steriruncic 5-cube centered at the origin are coordinate permutations:
- (±1,±1,±1,±3,±5)
with an odd number of plus signs.
Images
| Coxeter plane | B5 | |
|---|---|---|
| Graph | 
| |
| Dihedral symmetry | ||
| Coxeter plane | D5 | D4 |
| Graph | 
|

|
| Dihedral symmetry | ||
| Coxeter plane | D3 | A3 |
| Graph | 
|

|
| Dihedral symmetry |
Steriruncicantic 5-cube
| Steriruncicantic 5-cube | |
|---|---|
| Type | uniform polyteron |
| Schläfli symbol |
|
| Coxeter-Dynkin diagram | |
| 4-faces | 82 |
| Cells | 720 |
| Faces | 2080 |
| Edges | 2400 |
| Vertices | 960 |
| Vertex figure | |
| Coxeter groups | D5, |
| Properties | convex |
Alternate names
- Great prismated hemipenteract (giphin) (Jonathan Bowers)
Cartesian coordinates
The Cartesian coordinates for the 960 vertices of a steriruncicantic 5-cube centered at the origin are coordinate permutations:
- (±1,±1,±3,±5,±7)
with an odd number of plus signs.
Images
| Coxeter plane | B5 | |
|---|---|---|
| Graph | 
| |
| Dihedral symmetry | ||
| Coxeter plane | D5 | D4 |
| Graph | 
|

|
| Dihedral symmetry | ||
| Coxeter plane | D3 | A3 |
| Graph | 
|

|
| Dihedral symmetry |
Related polytopes
This polytope is based on the 5-demicube, a part of a dimensional family of uniform polytopes called demihypercubes for being alternation of the hypercube family.
There are 23 uniform polytera (uniform 5-polytope) that can be constructed from the D5 symmetry of the 5-demicube, of which are unique to this family, and 15 are shared within the 5-cube family.
| D5 polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
 h{4,3,3,3} |
 h2{4,3,3,3} |
 h3{4,3,3,3} |
 h4{4,3,3,3} |
 h2,3{4,3,3,3} |
 h2,4{4,3,3,3} |
 h3,4{4,3,3,3} |
 h2,3,4{4,3,3,3} | ||||
References
- ^ Klitzing, Richard. "5D uniform polytopes (polytera)".
Further reading
- Coxeter, H. S. M. (1973). Regular Polytopes (3rd ed.). New York City: Dover. Retrieved 2022-05-19.
- Coxeter, H. S. M. (1995-05-17). Sherk, F. Arthur; McMullen, Peter; Thompson, Anthony C.; Weiss, Asia Ivić (eds.). Kaleidoscopes: Selected Writings of H.S.M. Coxeter. Canadian Mathematical Society Series of Monographs and Advanced Texts. John Wiley & Sons. ISBN 978-0-471-01003-6. LCCN 94047368. OCLC 632987525. OL 7598569M. Retrieved 2022-05-19.
- Coxeter, H. S. M. (1940-12-01). "Regular and Semi Regular Polytopes I". Mathematische Zeitschrift. 46. Springer Nature: 380–407. doi:10.1007/BF01181449. ISSN 1432-1823. S2CID 186237114. Retrieved 2022-05-19.
- Coxeter, H. S. M. (1985-12-01). "Regular and Semi-Regular Polytopes II". Mathematische Zeitschrift. 188 (4). Springer Nature: 559–591. doi:10.1007/BF01161657. ISSN 1432-1823. S2CID 120429557. Retrieved 2022-05-19.
- Coxeter, H. S. M. (1988-03-01). "Regular and Semi-Regular Polytopes III". Mathematische Zeitschrift. 200 (1). Springer Nature: 3–45. doi:10.1007/BF01161745. ISSN 1432-1823. S2CID 186237142. Retrieved 2022-05-19.
- Johnson, Norman W. (1991). Uniform Polytopes (Unfinished manuscript thesis).
- Johnson, Norman W. (1966). The Theory of Uniform Polytopes and Honeycombs (PhD thesis). University of Toronto. Retrieved 2022-05-19.
External links
- Weisstein, Eric W. "Hypercube". MathWorld.
- Polytopes of Various Dimensions
- Multi-dimensional Glossary
| Fundamental convex regular and uniform polytopes in dimensions 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform polychoron | Pentachoron | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||