Misplaced Pages

Stoner criterion

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
(Redirected from Stoner model)
This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (October 2018) (Learn how and when to remove this message)

The Stoner criterion is a condition to be fulfilled for the ferromagnetic order to arise in a simplified model of a solid. It is named after Edmund Clifton Stoner.

Stoner model of ferromagnetism

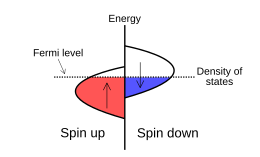
A schematic band structure for the Stoner model of ferromagnetism. An exchange interaction has split the energy of states with different spins, and states near the Fermi energy EF are spin-polarized.

Ferromagnetism ultimately stems from Pauli exclusion. The simplified model of a solid which is nowadays usually called the Stoner model, can be formulated in terms of dispersion relations for spin up and spin down electrons,

E ↑ ( k ) = ϵ ( k ) − I N ↑ − N ↓ N , E ↓ ( k ) = ϵ ( k ) + I N ↑ − N ↓ N , {\displaystyle E_{\uparrow }(k)=\epsilon (k)-I{\frac {N_{\uparrow }-N_{\downarrow }}{N}},\qquad E_{\downarrow }(k)=\epsilon (k)+I{\frac {N_{\uparrow }-N_{\downarrow }}{N}},}

where the second term accounts for the exchange energy, I {\displaystyle I} is the Stoner parameter, N ↑ / N {\displaystyle N_{\uparrow }/N} ( N ↓ / N {\displaystyle N_{\downarrow }/N} ) is the dimensionless density of spin up (down) electrons and ϵ ( k ) {\displaystyle \epsilon (k)} is the dispersion relation of spinless electrons where the electron-electron interaction is disregarded. If N ↑ + N ↓ {\displaystyle N_{\uparrow }+N_{\downarrow }} is fixed, E ↑ ( k ) , E ↓ ( k ) {\displaystyle E_{\uparrow }(k),E_{\downarrow }(k)} can be used to calculate the total energy of the system as a function of its polarization P = ( N ↑ − N ↓ ) / N {\displaystyle P=(N_{\uparrow }-N_{\downarrow })/N} . If the lowest total energy is found for P = 0 {\displaystyle P=0} , the system prefers to remain paramagnetic but for larger values of I {\displaystyle I} , polarized ground states occur. It can be shown that for

I D ( E F ) > 1 {\displaystyle ID(E_{\rm {F}})>1}

the P = 0 {\displaystyle P=0} state will spontaneously pass into a polarized one. This is the Stoner criterion, expressed in terms of the P = 0 {\displaystyle P=0} density of states at the Fermi energy D ( E F ) {\displaystyle D(E_{\rm {F}})} .

A non-zero P {\displaystyle P} state may be favoured over P = 0 {\displaystyle P=0} even before the Stoner criterion is fulfilled.

Relationship to the Hubbard model

The Stoner model can be obtained from the Hubbard model by applying the mean-field approximation. The particle density operators are written as their mean value ⟨ n i ⟩ {\displaystyle \langle n_{i}\rangle } plus fluctuation n i − ⟨ n i ⟩ {\displaystyle n_{i}-\langle n_{i}\rangle } and the product of spin-up and spin-down fluctuations is neglected. We obtain

H = U ∑ i [ n i , ↑ ⟨ n i , ↓ ⟩ + n i , ↓ ⟨ n i , ↑ ⟩ − ⟨ n i , ↑ ⟩ ⟨ n i , ↓ ⟩ ] − t ∑ ⟨ i , j ⟩ , σ ( c i , σ † c j , σ + h . c ) . {\displaystyle H=U\sum _{i}-t\sum _{\langle i,j\rangle ,\sigma }(c_{i,\sigma }^{\dagger }c_{j,\sigma }+h.c).}

With the third term included, which was omitted in the definition above, we arrive at the better-known form of the Stoner criterion

D ( E F ) U > 1. {\displaystyle D(E_{\rm {F}})U>1.}

Notes

  1. ^ Having a lattice model in mind, N {\textstyle N} is the number of lattice sites and N ↑ {\displaystyle N_{\uparrow }} is the number of spin-up electrons in the whole system. The density of states has the units of inverse energy. On a finite lattice, ϵ ( k ) {\displaystyle \epsilon (k)} is replaced by discrete levels ϵ i {\displaystyle \epsilon _{i}} and then D ( E ) = ∑ i δ ( E − ϵ i ) {\displaystyle D(E)=\sum _{i}\delta (E-\epsilon _{i})} .

References

Category: