| This article may be too technical for most readers to understand. Please help improve it to make it understandable to non-experts, without removing the technical details. (April 2022) (Learn how and when to remove this message) |
In category theory, a strong monad is a monad on a monoidal category with an additional natural transformation, called the strength, which governs how the monad interacts with the monoidal product.
Strong monads play an important role in theoretical computer science where they are used to model computation with side effects.
Definition
A (left) strong monad is a monad (T, η, μ) over a monoidal category (C, ⊗, I) together with a natural transformation tA,B : A ⊗ TB → T(A ⊗ B), called (tensorial) left strength, such that the diagrams
commute for every object A, B and C.
Commutative strong monads
For every strong monad T on a symmetric monoidal category, a right strength natural transformation can be defined by
A strong monad T is said to be commutative when the diagram
commutes for all objects and .
Properties
The Kleisli category of a commutative monad is symmetric monoidal in a canonical way, see corollary 7 in Guitart and corollary 4.3 in Power & Robison. When a monad is strong but not necessarily commutative, its Kleisli category is a premonoidal category.
One interesting fact about commutative strong monads is that they are "the same as" symmetric monoidal monads. More explicitly,
- a commutative strong monad defines a symmetric monoidal monad by
- and conversely a symmetric monoidal monad defines a commutative strong monad by
and the conversion between one and the other presentation is bijective.
References
- Moggi, Eugenio (July 1991). "Notions of computation and monads" (PDF). Information and Computation. 93 (1): 55–92. doi:10.1016/0890-5401(91)90052-4.
- Guitart, René (1980). "Tenseurs et machines". Cahiers de topologie et géométrie différentielle. 21 (1): 5–62. ISSN 2681-2398.
- Power, John; Robinson, Edmund (October 1997). "Premonoidal categories and notions of computation". Mathematical Structures in Computer Science. 7 (5): 453–468. doi:10.1017/S0960129597002375. ISSN 0960-1295.
- Kock, Anders (1972-12-01). "Strong functors and monoidal monads". Archiv der Mathematik. 23 (1): 113–120. doi:10.1007/BF01304852. ISSN 1420-8938.
External links
- Strong monad at the nLab





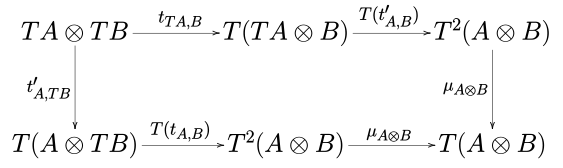
 and
and  .
.
 defines a symmetric monoidal monad
defines a symmetric monoidal monad  by
by
