Misplaced Pages

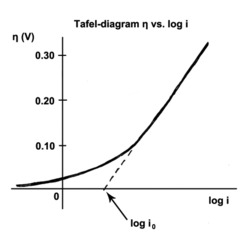
The Tafel equation is an equation in electrochemical kinetics relating the rate of an electrochemical reaction to the overpotential. The Tafel equation was first deduced experimentally and was later shown to have a theoretical justification. The equation is named after Swiss chemist Julius Tafel.

It describes how the electrical current through an electrode depends on the voltage difference between the electrode and the bulk electrolyte for a simple, unimolecular redox reaction.

${\displaystyle Ox+ne^{-}\leftrightarrows Red}$

Where an electrochemical reaction occurs in two half reactions on separate electrodes, the Tafel equation is applied to each electrode separately. On a single electrode the Tafel equation can be stated as:

${\displaystyle \eta =\pm A\cdot \log _{10}\left({\frac {i}{i_{0}}}\right)}$

(1)

where

• the plus sign under the exponent refers to an anodic reaction, and a minus sign to a cathodic reaction,
• ${\displaystyle \eta }$ : overpotential,
• ${\displaystyle A}$ : Tafel slope",
• ${\displaystyle i}$ : current density,
• ${\displaystyle i_{0}}$ : "exchange current density", .

A verification plus further explanation for this equation can be found here. The Tafel equation is an approximation of the Butler–Volmer equation in the case of ${\displaystyle |\eta |>0.1V}$.

" assumes that the concentrations at the electrode are practically equal to the concentrations in the bulk electrolyte, allowing the current to be expressed as a function of potential only. In other words, it assumes that the electrode mass transfer rate is much greater than the reaction rate, and that the reaction is dominated by the slower chemical reaction rate ".

Also, at a given electrode the Tafel equation assumes that the reverse half reaction rate is negligible compared to the forward reaction rate.

Overview of the terms

The exchange current is the current at equilibrium, i.e. the rate at which oxidized and reduced species transfer electrons with the electrode. In other words, the exchange current density is the rate of reaction at the reversible potential (when the overpotential is zero by definition). At the reversible potential, the reaction is in equilibrium meaning that the forward and reverse reactions progress at the same rates. This rate is the exchange current density.

The Tafel slope is measured experimentally. It can, however, be shown theoretically that when the dominant reaction mechanism involves the transfer of a single electron that $${\displaystyle {\frac {\lambda k_{\text{B}}T}{e}}<A}$$

where A is defined as

$${\displaystyle A={\frac {\lambda k_{\text{B}}T}{e\alpha }}={\frac {\lambda V_{T}}{\alpha }}}$$

(2)

where

• ${\displaystyle \lambda =\ln(10)=2.302\ 585...}$
• ${\displaystyle k_{\text{B}}}$ is the Boltzmann constant,
• ${\displaystyle T}$ is the absolute temperature,
• ${\displaystyle e}$ is the electric elementary charge of an electron,
• ${\displaystyle V_{T}=k_{\text{B}}T/e}$ is the thermal voltage, and
• ${\displaystyle \alpha }$ is the charge transfer coefficient, the value of which must be between 0 and 1.

Equation in case of non-negligible electrode mass transfer

In a more general case,

The following derivation of the extended Butler–Volmer equation is adapted from that of Bard and Faulkner and Newman and Thomas-Alyea. the current is expressed as a function not only of potential (as in the simple version), but of the given concentrations as well. The mass-transfer rate may be relatively small, but its only effect on the chemical reaction is through the altered (given) concentrations. In effect, the concentrations are a function of the potential as well.

The Tafel equation can be also written as:

$${\displaystyle i=nkFC\exp \left(\pm \alpha F{\frac {\eta }{RT}}\right)}$$

(3)

where

• n is the number of electrons exchanged, like in the Nernst equation,
• k is the rate constant for the electrode reaction in s,
• F is the Faraday constant,
• C is the reactive species concentration at the electrode surface in mol/m,
• the plus sign under the exponent refers to an anodic reaction, and a minus sign to a cathodic reaction,
• R is the universal gas constant.
• ${\displaystyle \alpha }$ is the charge transfer coefficient, the value of which must be between 0 and 1.

Demonstration

As seen in equation (1), $${\displaystyle \eta =\pm A\cdot \log _{10}\left({\frac {i}{i_{0}}}\right)}$$ $${\displaystyle \eta =\pm A\cdot {\frac {\ln \left({\frac {i}{i_{0}}}\right)}{\ln(10)}},}$$ so: $${\displaystyle i=i_{0}\exp \left(\pm {\frac {\ln(10)\eta }{A}}\right)}$$ $${\displaystyle i=i_{0}\exp \left(\pm \alpha e{\frac {\eta }{kT}}\right),}$$ as seen in equation (2) and because ${\displaystyle \lambda =\ln(10)}$. $${\displaystyle i=i_{0}\exp \left(\pm \alpha F{\frac {\eta }{RT}}\right)}$$ because ${\displaystyle {\frac {e}{k}}={\frac {e/Na}{k/Na}}={\frac {F}{R}}}$ due to the electrode mass transfer ${\displaystyle i_{0}=nkFC}$, which finally yields equation (3).

Equation in case of low values of polarization

An other equation is applicable at low values of polarization ${\displaystyle |\eta |\simeq 0V}$. In such case, the dependence of current on polarization is usually linear (not logarithmic):

${\displaystyle i=i_{0}{\frac {nF}{RT}}\Delta E}$

This linear region is called polarization resistance due to its formal similarity to Ohm's law.

Kinetics of corrosion

The pace at which corrosion develops is determined by the kinetics of the reactions involved, hence the electrical double layer is critical.

Applying an overpotential to an electrode causes the reaction to move in one direction, away from equilibrium. Tafel's law determines the new rate, and as long as the reaction kinetics are under control, the overpotential is proportional to the log of the corrosion current.

See also

• Overpotential
• Butler–Volmer equation
• Electrocatalyst
• Faradaic current
• Faraday's laws of electrolysis

References

1. Bard, A. J.; Faulkner, L. R. “Electrochemical Methods. Fundamentals and Applications” 2nd Ed. Wiley, New York. 2001. ISBN 0-471-04372-9
2. "Applicability".
3. "Tafel Slope for Anodic Reaction from Tafel Equation Calculator | Calculate Tafel Slope for Anodic Reaction from Tafel Equation". www.calculatoratoz.com. Retrieved 2024-05-28.
4. ^ "Limiting cases of Butler–Volmer equation".
5. "Tafel Slope for Cathodic Reaction from Tafel Equation Calculator | Calculate Tafel Slope for Cathodic Reaction from Tafel Equation". www.calculatoratoz.com. Retrieved 2024-05-28.
6. "Verification of Tafel Equation".
7. ^ "Applicability".
8. "Derivation of the extended Butler–Volmer equation".
9. "Connection between the Avogadro constant and the Boltzmann constant".
10. "Link between the Avogadro constant Na and the Faraday constant F".
11. "Expression in terms of the standard rate constant k=k0".
12. "Kinetics of Corrosion - the Tafel Equation". www.doitpoms.ac.uk. Retrieved 2024-05-28.

Further reading

• Burstein, G.T. (2005). "A century of Tafel's equation: 1905–2005 a commemorative issue of corrosion science". Corrosion Science. 47 (12): 2858–2870. doi:10.1016/j.corsci.2005.07.002.

External links

• Media related to Tafel equation at Wikimedia Commons

• Chemical kinetics
• Electrochemical equations
• Physical chemistry