Misplaced Pages

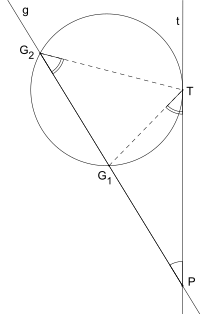
In Euclidean geometry, the tangent-secant theorem describes the relation of line segments created by a secant and a tangent line with the associated circle. This result is found as Proposition 36 in Book 3 of Euclid's Elements.

Given a secant g intersecting the circle at points G₁ and G₂ and a tangent t intersecting the circle at point T and given that g and t intersect at point P, the following equation holds:

$${\displaystyle |PT|^{2}=|PG_{1}|\cdot |PG_{2}|}$$

The tangent-secant theorem can be proven using similar triangles (see graphic).

Like the intersecting chords theorem and the intersecting secants theorem, the tangent-secant theorem represents one of the three basic cases of a more general theorem about two intersecting lines and a circle, namely, the power of point theorem.

References

• S. Gottwald: The VNR Concise Encyclopedia of Mathematics. Springer, 2012, ISBN 9789401169820, pp. 175-176
• Michael L. O'Leary: Revolutions in Geometry. Wiley, 2010, ISBN 9780470591796, p. 161
• Schülerduden - Mathematik I. Bibliographisches Institut & F.A. Brockhaus, 8. Auflage, Mannheim 2008, ISBN 978-3-411-04208-1, pp. 415-417 (German)

External links

• Tangent Secant Theorem at proofwiki.org
• Power of a Point Theorem auf cut-the-knot.org
• Weisstein, Eric W. "Chord". MathWorld.

v t e Ancient Greek mathematics
Mathematicians (timeline)	Anaxagoras Anthemius Archytas Aristaeus the Elder Aristarchus Aristotle Apollonius Archimedes Autolycus Bion Bryson Callippus Carpus Chrysippus Cleomedes Conon Ctesibius Democritus Dicaearchus Diocles Diophantus Dinostratus Dionysodorus Domninus Eratosthenes Eudemus Euclid Eudoxus Eutocius Geminus Heliodorus Heron Hipparchus Hippasus Hippias Hippocrates Hypatia Hypsicles Isidore of Miletus Leon Marinus Menaechmus Menelaus Metrodorus Nicomachus Nicomedes Nicoteles Oenopides Pappus Perseus Philolaus Philon Philonides Plato Porphyry Posidonius Proclus Ptolemy Pythagoras Serenus Simplicius Sosigenes Sporus Thales Theaetetus Theano Theodorus Theodosius Theon of Alexandria Theon of Smyrna Thymaridas Xenocrates Zeno of Elea Zeno of Sidon Zenodorus
Treatises	Almagest Archimedes Palimpsest Arithmetica Conics (Apollonius) Catoptrics Data (Euclid) Elements (Euclid) Measurement of a Circle On Conoids and Spheroids On the Sizes and Distances (Aristarchus) On Sizes and Distances (Hipparchus) On the Moving Sphere (Autolycus) Optics (Euclid) On Spirals On the Sphere and Cylinder Ostomachion Planisphaerium Spherics (Theodosius) Spherics (Menelaus) The Quadrature of the Parabola The Sand Reckoner
Problems	Constructible numbers Angle trisection Doubling the cube Squaring the circle Problem of Apollonius
Concepts and definitions	Angle Central Inscribed Axiomatic system Axiom Chord Circles of Apollonius Apollonian circles Apollonian gasket Circumscribed circle Commensurability Diophantine equation Doctrine of proportionality Euclidean geometry Golden ratio Greek numerals Incircle and excircles of a triangle Method of exhaustion Parallel postulate Platonic solid Lune of Hippocrates Quadratrix of Hippias Regular polygon Straightedge and compass construction Triangle center
Results	In Elements Angle bisector theorem Exterior angle theorem Euclidean algorithm Euclid's theorem Geometric mean theorem Greek geometric algebra Hinge theorem Inscribed angle theorem Intercept theorem Intersecting chords theorem Intersecting secants theorem Law of cosines Pons asinorum Pythagorean theorem Tangent-secant theorem Thales's theorem Theorem of the gnomon Apollonius Apollonius's theorem Other Aristarchus's inequality Crossbar theorem Heron's formula Irrational numbers Law of sines Menelaus's theorem Pappus's area theorem Problem II.8 of Arithmetica Ptolemy's inequality Ptolemy's table of chords Ptolemy's theorem Spiral of Theodorus
Centers	Cyrene Mouseion of Alexandria Platonic Academy
Related	Ancient Greek astronomy Attic numerals Greek numerals Latin translations of the 12th century Non-Euclidean geometry Philosophy of mathematics Neusis construction History of A History of Greek Mathematics by Thomas Heath algebra timeline arithmetic timeline calculus timeline geometry timeline logic timeline mathematics timeline numbers prehistoric counting numeral systems list Other cultures Arabian/Islamic Babylonian Chinese Egyptian Incan Indian Japanese
Ancient Greece portal • Mathematics portal

• Theorems about circles