Misplaced Pages

Thermodynamics
The classical Carnot heat engine
Branches Classical Statistical Chemical Quantum thermodynamics Equilibrium / Non-equilibrium
Laws Zeroth First Second Third
Systems Closed system Open system Isolated system State Equation of state Ideal gas Real gas State of matter Phase (matter) Equilibrium Control volume Instruments Processes Isobaric Isochoric Isothermal Adiabatic Isentropic Isenthalpic Quasistatic Polytropic Free expansion Reversibility Irreversibility Endoreversibility Cycles Heat engines Heat pumps Thermal efficiency
System propertiesNote: Conjugate variables in italics Property diagrams Intensive and extensive properties Process functions Work Heat Functions of state Temperature / Entropy (introduction) Pressure / Volume Chemical potential / Particle number Vapor quality Reduced properties
Material properties Property databases Specific heat capacity  ${\displaystyle c=}$ ${\displaystyle T}$ ${\displaystyle \partial S}$ ${\displaystyle N}$ ${\displaystyle \partial T}$ Compressibility  ${\displaystyle \beta =-}$ ${\displaystyle 1}$ ${\displaystyle \partial V}$ ${\displaystyle V}$ ${\displaystyle \partial p}$ Thermal expansion  ${\displaystyle \alpha =}$ ${\displaystyle 1}$ ${\displaystyle \partial V}$ ${\displaystyle V}$ ${\displaystyle \partial T}$
Equations Carnot's theorem Clausius theorem Fundamental relation Ideal gas law Maxwell relations Onsager reciprocal relations Bridgman's equations Table of thermodynamic equations
Potentials Free energy Free entropy Internal energy ${\displaystyle U(S,V)}$ Enthalpy ${\displaystyle H(S,p)=U+pV}$ Helmholtz free energy ${\displaystyle A(T,V)=U-TS}$ Gibbs free energy ${\displaystyle G(T,p)=H-TS}$
History Culture History General Entropy Gas laws "Perpetual motion" machines Philosophy Entropy and time Entropy and life Brownian ratchet Maxwell's demon Heat death paradox Loschmidt's paradox Synergetics Theories Caloric theory Vis viva ("living force") Mechanical equivalent of heat Motive power Key publications An Inquiry Concerning the Source ... Friction On the Equilibrium of Heterogeneous Substances Reflections on the Motive Power of Fire Timelines Thermodynamics Heat engines Art Education Maxwell's thermodynamic surface Entropy as energy dispersal
Scientists Bernoulli Boltzmann Bridgman Carathéodory Carnot Clapeyron Clausius de Donder Duhem Gibbs von Helmholtz Joule Kelvin Lewis Massieu Maxwell von Mayer Nernst Onsager Planck Rankine Smeaton Stahl Tait Thompson van der Waals Waterston
Other Nucleation Self-assembly Self-organization Order and disorder
Category
v t e

A thermodynamic cycle consists of linked sequences of thermodynamic processes that involve transfer of heat and work into and out of the system, while varying pressure, temperature, and other state variables within the system, and that eventually returns the system to its initial state. In the process of passing through a cycle, the working fluid (system) may convert heat from a warm source into useful work, and dispose of the remaining heat to a cold sink, thereby acting as a heat engine. Conversely, the cycle may be reversed and use work to move heat from a cold source and transfer it to a warm sink thereby acting as a heat pump. If at every point in the cycle the system is in thermodynamic equilibrium, the cycle is reversible. Whether carried out reversible or irreversibly, the net entropy change of the system is zero, as entropy is a state function.

During a closed cycle, the system returns to its original thermodynamic state of temperature and pressure. Process quantities (or path quantities), such as heat and work are process dependent. For a cycle for which the system returns to its initial state the first law of thermodynamics applies:

${\displaystyle \Delta U=E_{in}-E_{out}=0}$

The above states that there is no change of the internal energy (${\displaystyle U}$) of the system over the cycle. ${\displaystyle E_{in}}$ represents the total work and heat input during the cycle and ${\displaystyle E_{out}}$ would be the total work and heat output during the cycle. The repeating nature of the process path allows for continuous operation, making the cycle an important concept in thermodynamics. Thermodynamic cycles are often represented mathematically as quasistatic processes in the modeling of the workings of an actual device.

Heat and work

Two primary classes of thermodynamic cycles are power cycles and heat pump cycles. Power cycles are cycles which convert some heat input into a mechanical work output, while heat pump cycles transfer heat from low to high temperatures by using mechanical work as the input. Cycles composed entirely of quasistatic processes can operate as power or heat pump cycles by controlling the process direction. On a pressure–volume (PV) diagram or temperature–entropy diagram, the clockwise and counterclockwise directions indicate power and heat pump cycles, respectively.

Relationship to work

Because the net variation in state properties during a thermodynamic cycle is zero, it forms a closed loop on a P-V diagram. A P-V diagram's abscissa, Y axis, shows pressure (P) and ordinate, X axis, shows volume (V). The area enclosed by the loop is the net work (${\displaystyle W_{net}}$) done by the processes, i.e. the cycle:

${\displaystyle {\text{(1)}}\qquad W_{net}=\oint P\ dV}$

This work is equal to the net heat (Q) transferred into and out of the system:

${\displaystyle {\text{(2)}}\qquad W_{net}=Q_{net}=Q_{in}-Q_{out}}$

Equation (2) is consistent with the First Law; even though the internal energy changes during the course of the cyclic process, when the cyclic process finishes the system's internal energy is the same as the energy it had when the process began.

If the cyclic process moves clockwise around the loop, then ${\displaystyle W_{net}}$ will be positive, the cyclic machine will transform part of the heat exchanged into work and it represents a heat engine. If it moves counterclockwise, then ${\displaystyle W_{net}}$ will be negative, the cyclic machine will require work to absorb heat at a low temperature and reject it at a higher temperature and it represents a heat pump.

A list of thermodynamic processes

The following processes are often used to describe different stages of a thermodynamic cycle:

• Adiabatic : No energy transfer as heat (${\displaystyle Q}$) during that part of the cycle (${\displaystyle \delta Q=0}$). Energy transfer is considered as work done by the system only.
• Isothermal : The process is at a constant temperature during that part of the cycle (${\displaystyle T=\mathrm {constant} }$, ${\displaystyle dT=0}$). Energy transfer is considered as heat removed from or work done by the system.
• Isobaric : Pressure in that part of the cycle will remain constant. (${\displaystyle P=\mathrm {constant} }$, ${\displaystyle dP=0}$). Energy transfer is considered as heat removed from or work done by the system.
• Isochoric : The process is constant volume (${\displaystyle V=\mathrm {constant} }$, ${\displaystyle dV=0}$). Energy transfer is considered as heat removed from the system, as the work done by the system is zero.
• Isentropic : The process is one of constant entropy (${\displaystyle S=\mathrm {constant} }$, ${\displaystyle dS=0}$). It is adiabatic (no heat nor mass exchange) and reversible.
• Isenthalpic : The process that proceeds without any change in enthalpy or specific enthalpy.
• Polytropic : The process that obeys the relation ${\displaystyle PV^{n}=\mathrm {constant} }$.
• Reversible : The process where the net entropy production is zero; ${\displaystyle dS-{\frac {\delta Q}{T}}=0}$.

Example: The Otto cycle

The Otto Cycle is an example of a reversible thermodynamic cycle.

• 1→2: Isentropic / adiabatic expansion: Constant entropy (s), Decrease in pressure (P), Increase in volume (v), Decrease in temperature (T)
• 2→3: Isochoric cooling: Constant volume(v), Decrease in pressure (P), Decrease in entropy (S), Decrease in temperature (T)
• 3→4: Isentropic / adiabatic compression: Constant entropy (s), Increase in pressure (P), Decrease in volume (v), Increase in temperature (T)
• 4→1: Isochoric heating: Constant volume (v), Increase in pressure (P), Increase in entropy (S), Increase in temperature (T)

Power cycles

Thermodynamic power cycles are the basis for the operation of heat engines, which supply most of the world's electric power and run the vast majority of motor vehicles. Power cycles can be organized into two categories: real cycles and ideal cycles. Cycles encountered in real world devices (real cycles) are difficult to analyze because of the presence of complicating effects (friction), and the absence of sufficient time for the establishment of equilibrium conditions. For the purpose of analysis and design, idealized models (ideal cycles) are created; these ideal models allow engineers to study the effects of major parameters that dominate the cycle without having to spend significant time working out intricate details present in the real cycle model.

Power cycles can also be divided according to the type of heat engine they seek to model. The most common cycles used to model internal combustion engines are the Otto cycle, which models gasoline engines, and the Diesel cycle, which models diesel engines. Cycles that model external combustion engines include the Brayton cycle, which models gas turbines, the Rankine cycle, which models steam turbines, the Stirling cycle, which models hot air engines, and the Ericsson cycle, which also models hot air engines.

For example :--the pressure-volume mechanical work output from the ideal Stirling cycle (net work out), consisting of 4 thermodynamic processes, is:

${\displaystyle {\text{(3)}}\qquad W_{\rm {net}}=W_{1\to 2}+W_{2\to 3}+W_{3\to 4}+W_{4\to 1}}$

${\displaystyle W_{1\to 2}=\int _{V_{1}}^{V_{2}}P\,dV,\,\,{\text{negative, work done on system}}}$

${\displaystyle W_{2\to 3}=\int _{V_{2}}^{V_{3}}P\,dV,\,\,{\text{zero work since }}V_{2}=V_{3}}$

${\displaystyle W_{3\to 4}=\int _{V_{3}}^{V_{4}}P\,dV,\,\,{\text{positive, work done by system}}}$

${\displaystyle W_{4\to 1}=\int _{V_{4}}^{V_{1}}P\,dV,\,\,{\text{zero work since }}V_{4}=V_{1}}$

For the ideal Stirling cycle, no volume change happens in process 4-1 and 2-3, thus equation (3) simplifies to:

${\displaystyle {\text{(4)}}\qquad W_{\rm {net}}=W_{1\to 2}+W_{3\to 4}}$

Heat pump cycles

Thermodynamic heat pump cycles are the models for household heat pumps and refrigerators. There is no difference between the two except the purpose of the refrigerator is to cool a very small space while the household heat pump is intended to warm or cool a house. Both work by moving heat from a cold space to a warm space. The most common refrigeration cycle is the vapor compression cycle, which models systems using refrigerants that change phase. The absorption refrigeration cycle is an alternative that absorbs the refrigerant in a liquid solution rather than evaporating it. Gas refrigeration cycles include the reversed Brayton cycle and the Hampson–Linde cycle. Multiple compression and expansion cycles allow gas refrigeration systems to liquify gases.

Modeling real systems

Thermodynamic cycles may be used to model real devices and systems, typically by making a series of assumptions to reduce the problem to a more manageable form. For example, as shown in the figure, devices such a gas turbine or jet engine can be modeled as a Brayton cycle. The actual device is made up of a series of stages, each of which is itself modeled as an idealized thermodynamic process. Although each stage which acts on the working fluid is a complex real device, they may be modelled as idealized processes which approximate their real behavior. If energy is added by means other than combustion, then a further assumption is that the exhaust gases would be passed from the exhaust to a heat exchanger that would sink the waste heat to the environment and the working gas would be reused at the inlet stage.

The difference between an idealized cycle and actual performance may be significant. For example, the following images illustrate the differences in work output predicted by an ideal Stirling cycle and the actual performance of a Stirling engine:

Ideal Stirling cycle	Actual performance	Actual and ideal overlaid, showing difference in work output

As the net work output for a cycle is represented by the interior of the cycle, there is a significant difference between the predicted work output of the ideal cycle and the actual work output shown by a real engine. It may also be observed that the real individual processes diverge from their idealized counterparts; e.g., isochoric expansion (process 1-2) occurs with some actual volume change.

Well-known thermodynamic cycles

In practice, simple idealized thermodynamic cycles are usually made out of four thermodynamic processes. Any thermodynamic processes may be used. However, when idealized cycles are modeled, often processes where one state variable is kept constant, such as:

• adiabatic (constant heat)
• isothermal (constant temperature)
• isobaric (constant pressure)
• isochoric (constant volume)
• isentropic (constant entropy)
• isenthalpic (constant enthalpy)

Some example thermodynamic cycles and their constituent processes are as follows:

Ideal cycle

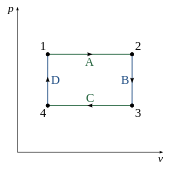
An ideal cycle is simple to analyze and consists of:

1. TOP (A) and BOTTOM (C) of the loop: a pair of parallel isobaric processes
2. RIGHT (B) and LEFT (D) of the loop: a pair of parallel isochoric processes

If the working substance is a perfect gas, ${\displaystyle U}$ is only a function of ${\displaystyle T}$ for a closed system since its internal pressure vanishes. Therefore, the internal energy changes of a perfect gas undergoing various processes connecting initial state ${\displaystyle a}$ to final state ${\displaystyle b}$ are always given by the formula

${\displaystyle \Delta U=\int _{a}^{b}C_{v}dT}$

Assuming that ${\displaystyle C_{v}}$ is constant, ${\displaystyle \Delta U=C_{v}\Delta T}$ for any process undergone by a perfect gas.

Under this set of assumptions, for processes A and C we have ${\displaystyle W=p\Delta v}$ and ${\displaystyle Q=C_{p}\Delta T}$, whereas for processes B and D we have ${\displaystyle W=0}$ and ${\displaystyle Q=\Delta U=C_{v}\Delta T}$.

The total work done per cycle is ${\displaystyle W_{cycle}=p_{A}(v_{2}-v_{1})+p_{C}(v_{4}-v_{3})=p_{A}(v_{2}-v_{1})+p_{C}(v_{1}-v_{2})=(p_{A}-p_{C})(v_{2}-v_{1})}$, which is just the area of the rectangle. If the total heat flow per cycle is required, this is easily obtained. Since ${\displaystyle \Delta U_{cycle}=Q_{cycle}-W_{cycle}=0}$, we have ${\displaystyle Q_{cycle}=W_{cycle}}$.

Thus, the total heat flow per cycle is calculated without knowing the heat capacities and temperature changes for each step (although this information would be needed to assess the thermodynamic efficiency of the cycle).

Carnot cycle

The Carnot cycle is a cycle composed of the totally reversible processes of isentropic compression and expansion and isothermal heat addition and rejection. The thermal efficiency of a Carnot cycle depends only on the absolute temperatures of the two reservoirs in which heat transfer takes place, and for a power cycle is:

${\displaystyle \eta =1-{\frac {T_{L}}{T_{H}}}}$

where ${\displaystyle {T_{L}}}$ is the lowest cycle temperature and ${\displaystyle {T_{H}}}$ the highest. For Carnot power cycles the coefficient of performance for a heat pump is:

${\displaystyle \ COP=1+{\frac {T_{L}}{T_{H}-T_{L}}}}$

and for a refrigerator the coefficient of performance is:

${\displaystyle \ COP={\frac {T_{L}}{T_{H}-T_{L}}}}$

The second law of thermodynamics limits the efficiency and COP for all cyclic devices to levels at or below the Carnot efficiency. The Stirling cycle and Ericsson cycle are two other reversible cycles that use regeneration to obtain isothermal heat transfer.

Stirling cycle

A Stirling cycle is like an Otto cycle, except that the adiabats are replaced by isotherms. It is also the same as an Ericsson cycle with the isobaric processes substituted for constant volume processes.

1. TOP and BOTTOM of the loop: a pair of quasi-parallel isothermal processes
2. LEFT and RIGHT sides of the loop: a pair of parallel isochoric processes

Heat flows into the loop through the top isotherm and the left isochore, and some of this heat flows back out through the bottom isotherm and the right isochore, but most of the heat flow is through the pair of isotherms. This makes sense since all the work done by the cycle is done by the pair of isothermal processes, which are described by Q=W. This suggests that all the net heat comes in through the top isotherm. In fact, all of the heat which comes in through the left isochore comes out through the right isochore: since the top isotherm is all at the same warmer temperature ${\displaystyle T_{H}}$ and the bottom isotherm is all at the same cooler temperature ${\displaystyle T_{C}}$, and since change in energy for an isochore is proportional to change in temperature, then all of the heat coming in through the left isochore is cancelled out exactly by the heat going out the right isochore.

State functions and entropy

If Z is a state function then the balance of Z remains unchanged during a cyclic process:

${\displaystyle \oint dZ=0}$.

Entropy is a state function and is defined in an absolute sense through the Third Law of Thermodynamics as

${\displaystyle S=\int _{0}^{T}{dQ_{rev} \over T}}$

where a reversible path is chosen from absolute zero to the final state, so that for an isothermal reversible process

${\displaystyle \Delta S={Q_{rev} \over T}}$.

In general, for any cyclic process the state points can be connected by reversible paths, so that

${\displaystyle \oint dS=\oint {dQ_{rev} \over T}=0}$

meaning that the net entropy change of the working fluid over a cycle is zero.

See also

• Entropy
• Economizer
• Thermogravitational cycle

References

1. Cengel, Yunus A.; Boles, Michael A. (2002). Thermodynamics: an engineering approach. Boston: McGraw-Hill. pp. 14. ISBN 0-07-238332-1.
2. ^ Cengel, Yunus A.; Boles, Michael A. (2002). Thermodynamics: an engineering approach. Boston: McGraw-Hill. pp. 452. ISBN 0-07-238332-1.

Further reading

• Halliday, Resnick & Walker. Fundamentals of Physics, 5th edition. John Wiley & Sons, 1997. Chapter 21, Entropy and the Second Law of Thermodynamics.
• Çengel, Yunus A., and Michael A. Boles. Thermodynamics: An Engineering Approach, 7th ed. New York: McGraw-Hill, 2011. Print.
• Hill and Peterson. "Mechanics and Thermodynamics of Propulsion", 2nd ed. Prentice Hall, 1991. 760 pp.

External links

• Thermodynamic cycles
• Equilibrium chemistry
• Thermodynamic processes
• Thermodynamic systems
• Thermodynamics