
The threshold voltage, commonly abbreviated as Vth or VGS(th), of a field-effect transistor (FET) is the minimum gate-to-source voltage (VGS) that is needed to create a conducting path between the source and drain terminals. It is an important scaling factor to maintain power efficiency.
When referring to a junction field-effect transistor (JFET), the threshold voltage is often called pinch-off voltage instead. This is somewhat confusing since pinch off applied to insulated-gate field-effect transistor (IGFET) refers to the channel pinching that leads to current saturation behavior under high source–drain bias, even though the current is never off. Unlike pinch off, the term threshold voltage is unambiguous and refers to the same concept in any field-effect transistor.
Basic principles
In n-channel enhancement-mode devices, a conductive channel does not exist naturally within the transistor. With no VGS, dopant ions added to the body of the FET form a region with no mobile carriers called a depletion region. A positive VGS attracts free-floating electrons within the body towards the gate. But enough electrons must be attracted near the gate to counter the dopant ions and form a conductive channel. This process is called inversion. The conductive channel connects from source to drain at the FET's threshold voltage. Even more electrons attract towards the gate at higher VGS, which widens the channel.
The reverse is true for the p-channel "enhancement-mode" MOS transistor. When VGS = 0 the device is “OFF” and the channel is open / non-conducting. The application of a negative gate voltage to the p-type "enhancement-mode" MOSFET enhances the channels conductivity turning it “ON”.
In contrast, n-channel depletion-mode devices have a conductive channel naturally existing within the transistor. Accordingly, the term threshold voltage does not readily apply to turning such devices on, but is used instead to denote the voltage level at which the channel is wide enough to allow electrons to flow easily. This ease-of-flow threshold also applies to p-channel depletion-mode devices, in which a negative voltage from gate to body/source creates a depletion layer by forcing the positively charged holes away from the gate-insulator/semiconductor interface, leaving exposed a carrier-free region of immobile, negatively charged acceptor ions.
For the n-channel depletion MOS transistor, a sufficient negative VGS will deplete (hence its name) the conductive channel of its free electrons switching the transistor “OFF”. Likewise for a p-channel "depletion-mode" MOS transistor a sufficient positive gate-source voltage will deplete the channel of its free holes, turning it “OFF”.
In wide planar transistors the threshold voltage is essentially independent of the drain–source voltage (VDS) and is therefore a well defined characteristic, however it is less clear in modern nanometer-sized MOSFETs due to drain-induced barrier lowering.
 Depletion region of an enhancement-mode nMOSFET biased below the threshold
Depletion region of an enhancement-mode nMOSFET biased below the threshold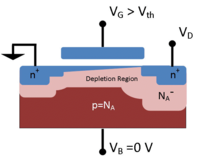 Depletion region of an enhancement-mode nMOSFET biased above the threshold with channel formed
Depletion region of an enhancement-mode nMOSFET biased above the threshold with channel formed
In the figures, the source (left side) and drain (right side) are labeled n+ to indicate heavily doped (blue) n-regions. The depletion layer dopant is labeled NA to indicate that the ions in the (pink) depletion layer are negatively charged and there are very few holes. In the (red) bulk the number of holes p = NA making the bulk charge neutral.
If the gate voltage is below the threshold voltage (left figure), the "enhancement-mode" transistor is turned off and ideally there is no current from the drain to the source of the transistor. In fact, there is a current even for gate biases below the threshold (subthreshold leakage) current, although it is small and varies exponentially with gate bias. Therefore, datasheets will specify threshold voltage according to a specified measurable amount of current (commonly 250 μA or 1 mA).
If the gate voltage is above the threshold voltage (right figure), the "enhancement-mode" transistor is turned on, due to there being many electrons in the channel at the oxide-silicon interface, creating a low-resistance channel where charge can flow from drain to source. For voltages significantly above the threshold, this situation is called strong inversion. The channel is tapered when VD > 0 because the voltage drop due to the current in the resistive channel reduces the oxide field supporting the channel as the drain is approached.
Body effect
The body effect is the change in the threshold voltage by an amount approximately equal to the change in the source-bulk voltage, , because the body influences the threshold voltage (when it is not tied to the source). It can be thought of as a second gate, and is sometimes referred to as the back gate, and accordingly the body effect is sometimes called the back-gate effect.
For an enhancement-mode nMOS MOSFET, the body effect upon threshold voltage is computed according to the Shichman–Hodges model, which is accurate for older process nodes, using the following equation:
where;
is the threshold voltage when substrate bias is present,
is the source-to-body substrate bias,
is the surface potential,
is threshold voltage for zero substrate bias,
is the body effect parameter,
is oxide thickness,
is oxide permittivity,
is the permittivity of silicon,
is a doping concentration,
is elementary charge.
Dependence on oxide thickness
In a given technology node, such as the 90-nm CMOS process, the threshold voltage depends on the choice of oxide and on oxide thickness. Using the body formulas above, is directly proportional to , and , which is the parameter for oxide thickness.
Thus, the thinner the oxide thickness, the lower the threshold voltage. Although this may seem to be an improvement, it is not without cost; because the thinner the oxide thickness, the higher the subthreshold leakage current through the device will be. Consequently, the design specification for 90-nm gate-oxide thickness was set at 1 nm to control the leakage current. This kind of tunneling, called Fowler-Nordheim Tunneling.
where;
and are constants,
is the electric field across the gate oxide.
Before scaling the design features down to 90 nm, a dual-oxide approach for creating the oxide thickness was a common solution to this issue. With a 90 nm process technology, a triple-oxide approach has been adopted in some cases. One standard thin oxide is used for most transistors, another for I/O driver cells, and a third for memory-and-pass transistor cells. These differences are based purely on the characteristics of oxide thickness on threshold voltage of CMOS technologies.
Temperature dependence
As with the case of oxide thickness affecting threshold voltage, temperature has an effect on the threshold voltage of a CMOS device. Expanding on part of the equation in the body effect section
where;
is half the contact potential,
is the Boltzmann constant,
is temperature,
is the elementary charge,
is a doping parameter,
is the intrinsic doping parameter for the substrate.
We see that the surface potential has a direct relationship with the temperature. Looking above, that the threshold voltage does not have a direct relationship but is not independent of the effects. This variation is typically between −4 mV/K and −2 mV/K depending on doping level. For a change of 30 °C this results in significant variation from the 500 mV design parameter commonly used for the 90-nm technology node.
Dependence on random dopant fluctuation
Random dopant fluctuation (RDF) is a form of process variation resulting from variation in the implanted impurity concentration. In MOSFET transistors, RDF in the channel region can alter the transistor's properties, especially threshold voltage. In newer process technologies RDF has a larger effect because the total number of dopants is fewer.
Research works are being carried out in order to suppress the dopant fluctuation which leads to the variation of threshold voltage between devices undergoing same manufacturing process.
See also
References
- "Junction Field Effect Transistor (JFET)" (PDF). ETEE3212 Lecture Notes.
This is called the threshold, or pinch-off, voltage and occurs at vGS=VGS(OFF).
- Sedra, Adel S.; Smith, Kenneth C. "5.11 THE JUNCTION FIELD-EFFECT TRANSISTOR (JFET)" (PDF). Microelectronic Circuits.
For JFETs the threshold voltage is called the pinch-off voltage and is denoted VP.
- Marco Delaurenti, PhD dissertation, Design and optimization techniques of high-speed VLSI circuits (1999)) Archived 2014-11-10 at the Wayback Machine
- NanoDotTek Report NDT14-08-2007, 12 August 2007
- Sugii, Watanabe and Sugatani. Transistor Design for 90-nm Generation and Beyond. (2002)
- S. M. Sze, Physics of Semiconductor Devices, Second Edition, New York: Wiley and Sons, 1981, pp. 496–504.
- Anil Telikepalli, Xilinx Inc, Power considerations in designing with 90 nm FPGAs (2005))
- Weste and Eshraghian, Principles of CMOS VLSI Design : a systems perspective, Second Edition, (1993) pp.48 ISBN 0-201-53376-6
- Asenov, A. Huang,Random dopant induced threshold voltage lowering and fluctuations in sub-0.1 μm MOSFET's: A 3-D “atomistic” simulation study, Electron Devices, IEEE Transactions, 45, Issue: 12
- Asenov, A. Huang,Suppression of random dopant-induced threshold voltage fluctuations in sub-0.1-μm MOSFET's with epitaxial and δ-doped channels, Electron Devices, IEEE Transactions, 46, Issue: 8
External links
- Online lecture on: Threshold Voltage and MOSFET Capacitances by Dr. Lundstrom
 , because the body influences the threshold voltage (when it is not tied to the source). It can be thought of as a second gate, and is sometimes referred to as the back gate, and accordingly the body effect is sometimes called the back-gate effect.
, because the body influences the threshold voltage (when it is not tied to the source). It can be thought of as a second gate, and is sometimes referred to as the back gate, and accordingly the body effect is sometimes called the back-gate effect.

 is the threshold voltage when substrate bias is present,
is the threshold voltage when substrate bias is present,
 is the surface potential,
is the surface potential,
 is threshold voltage for zero substrate bias,
is threshold voltage for zero substrate bias,
 is the body effect parameter,
is the body effect parameter,
 is oxide thickness,
is oxide thickness,
 is oxide permittivity,
is oxide permittivity,
 is the permittivity of silicon,
is the permittivity of silicon,
 is a doping concentration,
is a doping concentration,
 is elementary charge.
is elementary charge.
 , and
, and  , which is the parameter for oxide thickness.
, which is the parameter for oxide thickness.

 and
and  are constants,
are constants,
 is the electric field across the gate oxide.
is the electric field across the gate oxide.

 is half the contact potential,
is half the contact potential,
 is the
is the  is temperature,
is temperature,
 is the intrinsic doping parameter for the substrate.
is the intrinsic doping parameter for the substrate.