Misplaced Pages

In metric geometry, the metric envelope or tight span of a metric space M is an injective metric space into which M can be embedded. In some sense it consists of all points "between" the points of M, analogous to the convex hull of a point set in a Euclidean space. The tight span is also sometimes known as the injective envelope or hyperconvex hull of M. It has also been called the injective hull, but should not be confused with the injective hull of a module in algebra, a concept with a similar description relative to the category of R-modules rather than metric spaces.

The tight span was first described by Isbell (1964), and it was studied and applied by Holsztyński in the 1960s. It was later independently rediscovered by Dress (1984) and Chrobak & Larmore (1994); see Chepoi (1997) for this history. The tight span is one of the central constructions of T-theory.

Definition

The tight span of a metric space can be defined as follows. Let (X,d) be a metric space, and let T(X) be the set of extremal functions on X, where we say an extremal function on X to mean a function f from X to R such that

1. For any x, y in X, d(x,y) ≤ f(x) + f(y), and
2. For each x in X, f(x) = sup{d(x,y) - f(y):y in X}.

In particular (taking x = y in property 1 above) f(x) ≥ 0 for all x. One way to interpret the first requirement above is that f defines a set of possible distances from some new point to the points in X that must satisfy the triangle inequality together with the distances in (X,d). The second requirement states that none of these distances can be reduced without violating the triangle inequality.

The tight span of (X,d) is the metric space (T(X),δ), where $${\displaystyle \delta =(\inf\{C\in \mathbb {R} _{\geq 0}:|g(x)-f(x)|\leq C{\text{ for all }}x\in X\})_{f,g\in T(X)}=(\|g-f\|_{\infty })_{f,g\in T(X)}}$$ is analogous to the metric induced by the ℓ norm. (If d is bounded, then δ is the subspace metric induced by the metric induced by the ℓ norm. If d is not bounded, then every extremal function on X is unbounded and so ${\displaystyle T(X)\not \subseteq \ell ^{\infty }(X).}$ Regardless, it will be true that for any f,g in T(X), the difference ${\displaystyle g-f}$ belongs to ${\displaystyle \ell ^{\infty }(X)}$, i.e., is bounded.)

Equivalent definitions of extremal functions

For a function f from X to R satisfying the first requirement, the following versions of the second requirement are equivalent:

• For each x in X, f(x) = sup{d(x,y) - f(y):y in X}.
• f is pointwise minimal with respect to the aforementioned first requirement, i.e., for any function g from X to R such that d(x,y) ≤ g(x) + g(y) for all x,y in X, if g≤f pointwise, then f=g.

Basic properties and examples

• For all x in X, ${\displaystyle 0\leq f(x).}$
• For each x in X, ${\displaystyle (d(x,y))_{y\in X}}$ is extremal. (Proof: Use symmetry and the triangle inequality.)
• If X is finite, then for any function f from X to R that satisfies the first requirement, the second requirement is equivalent to the condition that for each x in X, there exists y in X such that f(x) + f(y) = d(x,y). (If ${\displaystyle X=\emptyset ,}$ then both conditions are true. If ${\displaystyle X\neq \emptyset ,}$ then the supremum is achieved, and the first requirement implies the equivalence.)
• Say |X|=2, and choose distinct a, b such that X={a,b}. Then ${\displaystyle T(X)=\{f\in (\mathbb {R} _{\geq 0})^{X}:f(a)+f(b)=d(a,b)\}}$ is the convex hull of {{(a,1),(b,0)},{(a,0),(b,1)}}. [Add a picture. Caption: If X={0,1}, then ${\displaystyle T(X)=\{v\in (\mathbb {R} _{\geq 0})^{2}:v_{0}+v_{1}=d(0,1)\}}$ is the convex hull of {(0,1),(1,0)}.]
• Every extremal function f on X is Katetov: f satisfies the first requirement and ${\displaystyle \forall x,y\in X\quad f(x)\leq d(x,y)+f(y),}$ or equivalently, f satisfies the first requirement and ${\displaystyle \forall x,y\in X\quad |f(y)-f(x)|\leq d(x,y)}$ (is 1-Lipschitz), or equivalently, f satisfies the first requirement and ${\displaystyle \forall x\in X\quad \sup\{f(y)-d(x,y):y\in X\}=f(x).}$
• T(X)⊆C(X). (Lipschitz functions are continuous.)
• T(X) is equicontinuous. (Follows from every extremal function on X being 1-Lipschitz; cf. Equicontinuity#Examples.)
• Not every Katetov function on X is extremal. For example, let a, b be distinct, let X = {a,b}, let d = ()_{x,y in X} be the discrete metric on X, and let f = {(a,1),(b,2)}. Then f is Katetov but not extremal. (It is almost immediate that f is Katetov. f is not extremal because it fails the property in the third bullet of this section.)
• If d is bounded, then every f in T(X) is bounded. In fact, for every f in T(X), ${\displaystyle \|f\|_{\infty }\leq \|d\|_{\infty }.}$ (Note ${\displaystyle d\in \ell ^{\infty }(X\times X).}$) (Follows from the third equivalent property in the above section.)
• If d is unbounded, then every f in T(X) is unbounded. (Follows from the first requirement.)
• ${\displaystyle T(X)}$ is closed under pointwise limits. For any pointwise convergent ${\displaystyle f\in (T(X))^{\omega },}$ ${\displaystyle \lim f\in T(X).}$
• If (X,d) is compact, then (T(X),δ) is compact. (Proof: The extreme-value theorem implies that d, being continuous as a function ${\displaystyle X\times X\to \mathbb {R} ,}$ is bounded, so (see previous bullet) ${\displaystyle T(X)\subseteq \{f\in C(X):\|f\|_{\infty }\leq \|d\|_{\infty }\}}$ is a bounded subset of C(X). We have shown T(X) is equicontinuous, so the Arzelà–Ascoli theorem implies that T(X) is relatively compact. However, the previous bullet implies T(X) is closed under the ${\displaystyle \ell ^{\infty }}$ norm, since ${\displaystyle \ell ^{\infty }}$ convergence implies pointwise convergence. Thus T(X) is compact.)
• For any function g from X to R that satisfies the first requirement, there exists f in T(X) such that f≤g pointwise.
• For any extremal function f on X, ${\displaystyle \forall x\in X\quad f(x)=\sup\{|f(y)-d(x,y)|:y\in X\}.}$
• For any f,g in T(X), the difference ${\displaystyle g-f}$ belongs to ${\displaystyle \ell ^{\infty }(X)}$, i.e., is bounded. (Use the above bullet.)
• The Kuratowski map ${\displaystyle e:=((d(x,y))_{y\in X})_{x\in X}}$ is an isometry. (When X=∅, the result is obvious. When X≠∅, the reverse triangle inequality implies the result.)
• Let f in T(X). For any a in X, if f(a)=0, then f=e(a). (For every x in X we have ${\displaystyle (e(a))(x)=d(a,x)\leq f(a)+f(x)=f(x).}$ From minimality (second equivalent characterization in above section) of f and the fact that ${\displaystyle e(a)}$ satisfies the first requirement it follows that ${\displaystyle f=e_{a}.}$)
• (X,d) is hyperbolic if and only if (T(X),δ) is hyperbolic.

Hyperconvexity properties

• (T(X),δ) and $${\displaystyle \left(X\cup (T(X)\setminus \operatorname {range} e),\delta _{(T(X)\setminus \operatorname {range} e)\times (T(X)\setminus \operatorname {range} e)}\cup (\delta (e(x),e(y)))_{x,y\in X}\cup (\delta (e(x),g))_{x\in X,g\in T(X)\setminus \operatorname {range} e}\cup (\delta (f,e(y))_{f\in T(X)\setminus \operatorname {range} e,y\in X}\right)}$$ are both hyperconvex.
• For any Y such that ${\displaystyle \operatorname {range} e\subseteq Y\subsetneq X\cup (T(X)\setminus \operatorname {range} e),}$ $${\displaystyle \left(X\cup (Y\setminus \operatorname {range} e),\delta _{(Y\setminus \operatorname {range} e)\times (Y\setminus \operatorname {range} e)}\cup (\delta (e(x),e(y)))_{x,y\in X}\cup (\delta (e(x),g))_{x\in X,g\in Y\setminus \operatorname {range} e}\cup (\delta (f,e(y))_{f\in Y\setminus \operatorname {range} e,y\in X}\right)}$$ is not hyperconvex. ("(T(X),δ) is a hyperconvex hull of (X,d).")
• Let ${\displaystyle (H,\varepsilon )}$ be a hyperconvex metric space with ${\displaystyle X\subseteq H}$ and ${\displaystyle \varepsilon |_{X\times X}=\delta }$. If for all I with ${\displaystyle X\subseteq I\subsetneq H,}$ ${\displaystyle (I,\varepsilon |_{I\times I})}$ is not hyperconvex, then ${\displaystyle (H,\varepsilon )}$ and (T(X),δ) are isometric. ("Every hyperconvex hull of (X,d) is isometric with (T(X),δ).")

Examples

• Say |X|=3, choose distinct a, b, c such that X={a,b,c}, and let i=d(a,b), j=d(a,c), k=d(b,c). Then $${\displaystyle {\begin{alignedat}{2}T(X)=&\{v\in (\mathbb {R} _{\geq 0})^{3}:1=v_{a}+v_{b},2=v_{a}+v_{c},3\leq v_{b}+v_{c}\\&\qquad \qquad \qquad {\text{or }}1=v_{a}+v_{b},2\leq v_{a}+v_{c},3=v_{b}+v_{c}\\&\qquad \qquad \qquad {\text{or }}1\leq v_{a}+v_{b},2=v_{a}+v_{c},3=v_{b}+v_{c}\}\\=&\{v\in (\mathbb {R} _{\geq 0})^{3}:v_{a}\leq {\frac {(i+j)-k}{2}},v_{b}=i-v_{a},v_{c}=j-v_{a}\\&\qquad \qquad \qquad {\text{or }}v_{a}=i-v_{b},v_{b}\leq {\frac {(i+k)-j}{2}},v_{c}=k-v_{b}\\&\qquad \qquad \qquad {\text{or }}v_{a}=j-v_{c},v_{b}=k-v_{c},v_{c}\leq {\frac {(j+k)-i}{2}}\}\\=&\left\{(t,i-t,j-t):t\in \left\right\}\\&\cup \left\{(i-t,t,k-t):t\in \left\right\}\\&\cup \left\{(j-t,k-t,t):t\in \left\right\}\\=&\left\{(t,i-t,j-t):t\in \left\right\}\\&\cup \left\{(i-t,t,k-t):t\in \left\right\}\\&\cup \left\{(j-t,k-t,t):t\in \left\right\}\\=&\operatorname {conv} \{(0,i,j),x\}\cup \operatorname {conv} \{(i,0,k),x\}\cup \operatorname {conv} \{(j,k,0),x\},\end{alignedat}}}$$ where ${\displaystyle x=2^{-1}(i+j-k,i+k-j,j+k-i).}$ (Cf. )

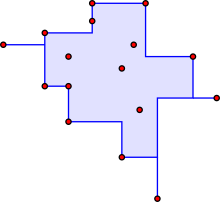
• The figure shows a set X of 16 points in the plane; to form a finite metric space from these points, we use the Manhattan distance (ℓ distance). The blue region shown in the figure is the orthogonal convex hull, the set of points z such that each of the four closed quadrants with z as apex contains a point of X. Any such point z corresponds to a point of the tight span: the function f(x) corresponding to a point z is f(x) = d(z,x). A function of this form satisfies property 1 of the tight span for any z in the Manhattan-metric plane, by the triangle inequality for the Manhattan metric. To show property 2 of the tight span, consider some point x in X; we must find y in X such that f(x)+f(y)=d(x,y). But if x is in one of the four quadrants having z as apex, y can be taken as any point in the opposite quadrant, so property 2 is satisfied as well. Conversely it can be shown that every point of the tight span corresponds in this way to a point in the orthogonal convex hull of these points. However, for point sets with the Manhattan metric in higher dimensions, and for planar point sets with disconnected orthogonal hulls, the tight span differs from the orthogonal convex hull.

Dimension of the tight span when X is finite

The definition above embeds the tight span T(X) of a set of n (${\displaystyle n\in \mathbb {Z} _{\geq 0}}$) points into R, a real vector space of dimension n. On the other hand, if we consider the dimension of T(X) as a polyhedral complex, Develin (2006) showed that, with a suitable general position assumption on the metric, this definition leads to a space with dimension between n/3 and n/2.

Alternative definitions

An alternative definition based on the notion of a metric space aimed at its subspace was described by Holsztyński (1968), who proved that the injective envelope of a Banach space, in the category of Banach spaces, coincides (after forgetting the linear structure) with the tight span. This theorem allows to reduce certain problems from arbitrary Banach spaces to Banach spaces of the form C(X), where X is a compact space.

Develin & Sturmfels (2004) attempted to provide an alternative definition of the tight span of a finite metric space as the tropical convex hull of the vectors of distances from each point to each other point in the space. However, later the same year they acknowledged in an Erratum Develin & Sturmfels (2004a) that, while the tropical convex hull always contains the tight span, it may not coincide with it.

Applications

• Dress, Huber & Moulton (2001) describe applications of the tight span in reconstructing evolutionary trees from biological data.
• The tight span serves a role in several online algorithms for the K-server problem.
• Sturmfels & Yu (2004) uses the tight span to classify metric spaces on up to six points.
• Chepoi (1997) uses the tight span to prove results about packing cut metrics into more general finite metric spaces.

See also

• Kuratowski embedding, an embedding of any metric space into a Banach space defined similarly to the Kuratowski map
• Injective metric space

Notes

1. Dress, Huber & Moulton (2001).
2. ^ Khamsi, Mohamed A.; Kirk, William A. (2001). An Introduction to Metric Spaces and Fixed Point Theory. Wiley.
3. ^ Dress, Andreas; Huber, Katharina T.; Koolen, Jacobus; Moulton, Vincent; Spillner, Andreas (2012). Basic Phylogenetic Combinatorics. Cambridge University Press. ISBN 978-0-521-76832-0.
4. ^ Huson, Daniel H.; Rupp, Regula; Scornavacca, Celine (2010). Phylogenetic Networks: Conceps, Algorithms and Applications. Cambridge University Press. ISBN 978-0-521-75596-2.
5. Deza, Michel Marie; Deza, Elena (2014). Encyclopedia of Distances (Third ed.). Springer. p. 47. ISBN 978-3-662-44341-5.
6. Melleray, Julien (2008). "Some geometric and dynamical properties of the Urysohn space". Topology and Its Applications. 155 (14): 1531–1560. doi:10.1016/j.topol.2007.04.029.
7. Benyamini, Yoav; Lindenstrauss, Joram (2000). Geometric Nonlinear Functional Analysis. American Mathematical Society. p. 32. ISBN 978-0-8218-0835-1.
8. In two dimensions, the Manhattan distance is isometric after rotation and scaling to the ℓ distance, so with this metric the plane is itself injective, but this equivalence between ℓ and ℓ does not hold in higher dimensions.
9. Chrobak & Larmore (1994).

1. Khamsi and Kirk use this condition in their definition.
2. Khamsi and Kirk's proof shows one implication of the equivalence to the condition immediately above. The other implication is not difficult to show.
3. I.e., the Kuratowski map ${\displaystyle e(x)\in T(X).}$ We will introduce the Kuratowski map below.
4. The supremum is achieved with y=x.
5. The supremum is achieved with y=x.

References

• Chepoi, Victor (1997), "A T_X approach to some results on cuts and metrics", Advances in Applied Mathematics, 19 (4): 453–470, doi:10.1006/aama.1997.0549.
• Chrobak, Marek; Larmore, Lawrence L. (1994), "Generosity helps or an 11-competitive algorithm for three servers", Journal of Algorithms, 16 (2): 234–263, doi:10.1006/jagm.1994.1011, S2CID 15169525.
• Develin, Mike (2006), "Dimensions of tight spans", Annals of Combinatorics, 10 (1): 53–61, arXiv:math.CO/0407317, doi:10.1007/s00026-006-0273-y, S2CID 92984638.
• Develin, Mike; Sturmfels, Bernd (2004), "Tropical convexity" (PDF), Documenta Mathematica, 9: 1–27, doi:10.4171/dm/154, S2CID 64471.
• Develin, Mike; Sturmfels, Bernd (2004a), "Erratum for "Tropical Convexity"" (PDF), Documenta Mathematica, 9: 205–206, doi:10.4171/dm/154, S2CID 64471.
• Dress, Andreas W. M. (1984), "Trees, tight extensions of metric spaces, and the cohomological dimension of certain groups", Advances in Mathematics, 53 (3): 321–402, doi:10.1016/0001-8708(84)90029-X.
• Dress, Andreas W. M.; Huber, K. T.; Moulton, V. (2001), "Metric spaces in pure and applied mathematics" (PDF), Documenta Mathematica (Proceedings Quadratic Forms LSU): 121–139.
• Holsztyński, Włodzimierz (1968), "Linearisation of isometric embeddings of Banach Spaces. Metric Envelopes.", Bull. Acad. Polon. Sci., 16: 189–193.
• Isbell, J. R. (1964), "Six theorems about injective metric spaces", Comment. Math. Helv., 39: 65–76, doi:10.1007/BF02566944, S2CID 121857986.
• Sturmfels, Bernd; Yu, Josephine (2004), "Classification of Six-Point Metrics", The Electronic Journal of Combinatorics, 11: R44, arXiv:math.MG/0403147, Bibcode:2004math......3147S, doi:10.37236/1797, S2CID 6733896.

External links

• Joswig, Michael, Tight spans.

• Metric geometry