In mathematics, the Coxeter complex, named after H. S. M. Coxeter, is a geometrical structure (a simplicial complex) associated to a Coxeter group. Coxeter complexes are the basic objects that allow the construction of buildings; they form the apartments of a building.
Construction
The canonical linear representation
The first ingredient in the construction of the Coxeter complex associated to a Coxeter system is a certain representation of , called the canonical representation of .
Let be a Coxeter system with Coxeter matrix . The canonical representation is given by a vector space with basis of formal symbols , which is equipped with the symmetric bilinear form . In particular, . The action of on is then given by .
This representation has several foundational properties in the theory of Coxeter groups; for instance, is positive definite if and only if is finite. It is a faithful representation of .
Chambers and the Tits cone
This representation describes as a reflection group, with the caveat that might not be positive definite. It becomes important then to distinguish the representation from its dual . The vectors lie in and have corresponding dual vectors in given by
where the angled brackets indicate the natural pairing between and .
Now acts on and the action is given by
for and any . Then is a reflection in the hyperplane . One has the fundamental chamber ; this has faces the so-called walls, . The other chambers can be obtained from by translation: they are the for .
The Tits cone is . This need not be the whole of . Of major importance is the fact that is convex. The closure of is a fundamental domain for the action of on .
The Coxeter complex
The Coxeter complex of with respect to is , where is the multiplicative group of positive reals.
Examples
Finite dihedral groups
The dihedral groups (of order 2n) are Coxeter groups, of corresponding type . These have the presentation .
The canonical linear representation of is the usual reflection representation of the dihedral group, as acting on an -gon in the plane (so in this case). For instance, in the case we get the Coxeter group of type , acting on an equilateral triangle in the plane. Each reflection has an associated hyperplane in the dual vector space (which can be canonically identified with the vector space itself using the bilinear form , which is an inner product in this case as remarked above); these are the walls. They cut out chambers, as seen below:
The Coxeter complex is then the corresponding -gon, as in the image above. This is a simplicial complex of dimension 1, and it can be colored by cotype.
The infinite dihedral group
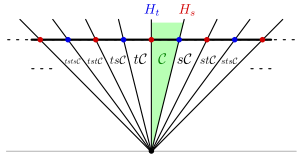
Another motivating example is the infinite dihedral group . This can be seen as the group of symmetries of the real line that preserves the set of points with integer coordinates; it is generated by the reflections in and . This group has the Coxeter presentation .
In this case, it is no longer possible to identify with its dual space , as is degenerate. It is then better to work solely with , which is where the hyperplanes are defined. This then gives the following picture:
In this case, the Tits cone is not the whole plane, but only the upper half plane. Taking the quotient by the positive reals then yields another copy of the real line, with marked points at the integers. This is the Coxeter complex of the infinite dihedral group.
Alternative construction of the Coxeter complex
Another description of the Coxeter complex uses standard cosets of the Coxeter group . A standard coset is a coset of the form , where for some proper subset of . For instance, and .
The Coxeter complex is then the poset of standard cosets, ordered by reverse inclusion. This has a canonical structure of a simplicial complex, as do all posets that satisfy:
- Any two elements have a greatest lower bound.
- The poset of elements less than or equal to any given element is isomorphic to the poset of subsets of for some integer n.
Properties
The Coxeter complex associated to has dimension . It is homeomorphic to a -sphere if W is finite and is contractible if W is infinite.
Every apartment of a spherical Tits building is a Coxeter complex.
See also
References
- https://dept.math.lsa.umich.edu/~lji/building-curve-complex-handbook.pdf pg. 8, definition 2.5
Sources
- Peter Abramenko and Kenneth S. Brown, Buildings, Theory and Applications. Springer, 2008.
 is a certain
is a certain  , called the canonical representation of
, called the canonical representation of  . The canonical representation is given by a vector space
. The canonical representation is given by a vector space  with basis of formal symbols
with basis of formal symbols  , which is equipped with the symmetric bilinear form
, which is equipped with the symmetric bilinear form  . In particular,
. In particular,  . The action of
. The action of  .
.
 is positive definite if and only if
is positive definite if and only if  . The vectors
. The vectors  lie in
lie in  in
in 

 and any
and any  . Then
. Then  is a reflection in the hyperplane
is a reflection in the hyperplane  . One has the fundamental chamber
. One has the fundamental chamber  ; this has faces the so-called walls,
; this has faces the so-called walls,  . The other chambers can be obtained from
. The other chambers can be obtained from  by translation: they are the
by translation: they are the  for
for  .
.
 . This need not be the whole of
. This need not be the whole of  is convex. The closure
is convex. The closure  of
of  of
of  is
is
 , where
, where  is the multiplicative group of positive reals.
is the multiplicative group of positive reals.
 (of order 2n) are Coxeter groups, of corresponding type
(of order 2n) are Coxeter groups, of corresponding type  . These have the presentation
. These have the presentation  .
.
 -gon in the plane (so
-gon in the plane (so  in this case). For instance, in the case
in this case). For instance, in the case  we get the Coxeter group of type
we get the Coxeter group of type  , acting on an equilateral triangle in the plane. Each reflection
, acting on an equilateral triangle in the plane. Each reflection 
 -gon, as in the image above. This is a simplicial complex of dimension 1, and it can be colored by cotype.
-gon, as in the image above. This is a simplicial complex of dimension 1, and it can be colored by cotype.
 . This can be seen as the group of symmetries of the real line that preserves the set of points with integer coordinates; it is generated by the reflections in
. This can be seen as the group of symmetries of the real line that preserves the set of points with integer coordinates; it is generated by the reflections in  and
and  . This group has the Coxeter presentation
. This group has the Coxeter presentation  .
.
 , where
, where  for some proper subset
for some proper subset  of
of  and
and  .
.
 for some integer n.
for some integer n. . It is homeomorphic to a
. It is homeomorphic to a  -sphere if W is finite and is
-sphere if W is finite and is