
The combinatorial game Toads and Frogs is a partisan game invented by Richard Guy. This mathematical game was used as an introductory game in the book Winning Ways for your Mathematical Plays.
Known for its simplicity and the elegance of its rules, Toads-and-Frogs is useful to illustrate the main concepts of combinatorial game theory. In particular, it is not difficult to evaluate simple games involving only one toad and one frog, by constructing the game tree of the starting position. However, the general case of evaluating an arbitrary position is known to be NP-hard. There are some open conjectures on the value of some remarkable positions.
A one-player puzzle version of the game has also been considered.
Rules
Toads and Frogs is played on a 1 × n strip of squares. At any time, each square is either empty or occupied by a single toad or frog. Although the game may start at any configuration, it is customary to begin with toads occupying consecutive squares on the leftmost end and frogs occupying consecutive squares on the rightmost end of the strip.
When it is the Left player's turn to move, they may either move a toad one square to the right, into an empty square, or "hop" a toad two squares to the right, over a frog, into an empty square. Hops over an empty square, a toad, or more than one square are not allowed. Analogous rules apply for Right: on a turn, the Right player may move a frog left into a neighboring empty space, or hop a frog over a single toad into an empty square immediately to the toad's left. Under the normal play rule conventional for combinatorial game theory, the first player to be unable to move on their turn loses.
Notation
A position of Toads-and-Frogs may be represented with a string of three characters : for a toad, for a frog, and for an empty space. For example, the string represents a strip of four squares with a toad on the first one, and a frog on the last one.
In combinatorial game theory, a position can be described recursively in terms of its options, i.e. the positions that the Left player and the Right player can move to. If Left can move from a position to the positions , , ... and Right to the positions , , ..., then the position is written conventionally
In this notation, for example, . This means that Left can move a toad one square to the right, and Right can move a frog one square to the left.
Game-theoretic values
Most of the research around Toads-and-Frogs has been around determining the game-theoretic values of some particular Toads-and-Frogs positions, or determining whether some particular values can arise in the game.
Winning Ways for your Mathematical Plays showed first numerous possible values. For example, :
In 1996, Jeff Erickson proved that for any dyadic rational number q (which are the only numbers that can arise in finite games), there exists a Toads-and-Frogs positions with value q. He also found an explicit formula for some remarkable positions, like , and formulated six conjectures on the values of other positions and the hardness of the game.
These conjectures fueled further research. Jesse Hull proved conjecture 6 in 2000, which states that determining the value of an arbitrary Toads-and-Frogs position is NP-hard. Doron Zeilberger and Thotsaporn Aek Thanatipanonda proved conjecture 1, 2 and 3 and found a counter-example to conjecture 4 in 2008. Conjecture 5, the last one still open, states that is an infinitesimal value, for all (a, b) except (3, 2).
Single-player puzzle
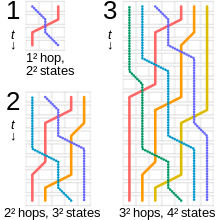
It is possible for a game of Toads and Frogs to end early. A one-player puzzle version of the Toads and Frogs game, published in 1883 by Édouard Lucas, asks for a sequence of moves beginning in the standard starting position that lasts as long as possible, ending with all of the toads on the right and all of the frogs on the left. The moves are not required to alternate between toads and frogs.
References
- ^ Berlekamp, Elwyn R.; Conway, John H.; Guy, Richard K. (2001), "Toads-and-Frogs", Winning Ways for your Mathematical Plays, vol. 1 (2nd ed.), A K Peters, pp. 12–13
- Erickson, Jeff (1996), "New Toads and Frogs results", in Nowakowski, Richard J. (ed.), Games of No Chance, Mathematical Sciences Research Institute Publications, vol. 29, Cambridge University Press, pp. 299–310
- As mentioned both by Erickson on his website and Thanatipanonda in his paper.
- Thanatipanonda, Thotsaporn (2011), "Further hopping with Toads and Frogs", Electronic Journal of Combinatorics, 18 (1): P67:1–P67:12, arXiv:0804.0640, doi:10.37236/554, MR 2788684, S2CID 35020735
- Levitin, Anany (2011). "Toads and Frogs". Algorithmic Puzzles. Oxford University Press. p. 53.
 for a toad,
for a toad,  for a frog, and
for a frog, and  for an empty space. For example, the string
for an empty space. For example, the string  represents a strip of four squares with a toad on the first one, and a frog on the last one.
represents a strip of four squares with a toad on the first one, and a frog on the last one.
 to the positions
to the positions  ,
,  , ... and Right to the positions
, ... and Right to the positions  ,
,  , ..., then the position
, ..., then the position 
 . This means that Left can move a toad one square to the right, and Right can move a frog one square to the left.
. This means that Left can move a toad one square to the right, and Right can move a frog one square to the left.





 , and formulated six conjectures on the values of other positions and the hardness of the game.
, and formulated six conjectures on the values of other positions and the hardness of the game.
 is an infinitesimal value, for all (a, b) except (3, 2).
is an infinitesimal value, for all (a, b) except (3, 2).