Misplaced Pages

Tridyakis icosahedron
Type	Star polyhedron
Face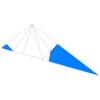
Elements	F = 120, E = 180 V = 44 (χ = −16)
Symmetry group	Ih, , *532
Index references	DU45
dual polyhedron	Icositruncated dodecadodecahedron

In geometry, the tridyakis icosahedron is the dual polyhedron of the nonconvex uniform polyhedron, icositruncated dodecadodecahedron. It has 44 vertices, 180 edges, and 120 scalene triangular faces.

Proportions

The triangles have one angle of ${\displaystyle \arccos({\frac {3}{5}})\approx 53.130\,102\,354\,16^{\circ }}$, one of ${\displaystyle \arccos({\frac {1}{3}}+{\frac {4}{15}}{\sqrt {5}})\approx 21.624\,633\,927\,143^{\circ }}$ and one of ${\displaystyle \arccos({\frac {1}{3}}-{\frac {4}{15}}{\sqrt {5}})\approx 105.245\,263\,718\,70^{\circ }}$. The dihedral angle equals ${\displaystyle \arccos(-{\frac {7}{8}})\approx 151.044\,975\,628\,14^{\circ }}$. Part of each triangle lies within the solid, hence is invisible in solid models.

See also

• Catalan solid Duals to convex uniform polyhedra
• Uniform polyhedra
• List of uniform polyhedra

References

• Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5, MR 0730208 Photo on page 96, Dorman Luke construction and stellation pattern on page 97.
• Weisstein, Eric W. "Tridyakis Icosahedron". MathWorld.

This polyhedron-related article is a stub. You can help Misplaced Pages by expanding it.

• v
• t
• e

• Dual uniform polyhedra
• Polyhedron stubs