Misplaced Pages

Tritos

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
Eclipse cycle
This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (October 2024) (Learn how and when to remove this message)
A graph of lunar eclipses, grouped by their Saros cycle and Tritos cycle

The tritos is an eclipse cycle of 3,986.628 days (about 10 years, 11 months). It corresponds to:

The length of the tritos is equal to the length of the inex minus the length of the saros eclipse cycles. Therefore, eclipses that occur 1 tritos apart (i.e. both eclipses belong to the same tritos series), belong to two different saros series with series numbers that differ by one.

The pre-Columbian Maya used a calculation in their own observations of eclipse cycles in which a period of three tritoses (or tritoi) was approximated by 11960 days, based on 46 periods of their tzolk'in calendar (i.e. 46 × 260 days). The number of anomalistic months in a tritos (144.68), having a fraction near 2⁄3, means every third eclipse is in nearly the same position in the elliptical orbit, so eclipses will have similar timing and total versus annular quality.

Solar and lunar eclipse event dates will repeat on this cycle for about 700 years.

Example solar Tritos series

This eclipse is a part of a tritos cycle, repeating at alternating nodes every 135 synodic months (≈ 3986.63 days, or 11 years minus 1 month). Their appearance and longitude are irregular due to a lack of synchronization with the anomalistic month (period of perigee), but groupings of 3 tritos cycles (≈ 33 years minus 3 months) come close (≈ 434.044 anomalistic months), so eclipses are similar in these groupings.

Series members between 1801 and 2200

December 21, 1805
(Saros 119)
November 19, 1816
(Saros 120)
October 20, 1827
(Saros 121)
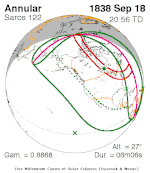September 18, 1838
(Saros 122)
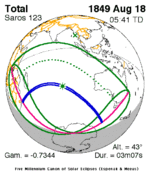August 18, 1849
(Saros 123)

July 18, 1860
(Saros 124)
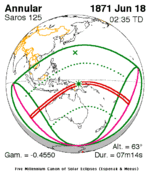June 18, 1871
(Saros 125)
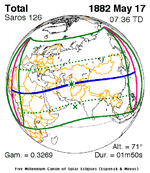May 17, 1882
(Saros 126)
April 16, 1893
(Saros 127)
March 17, 1904
(Saros 128)

February 14, 1915
(Saros 129)
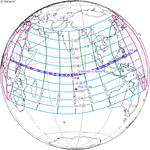January 14, 1926
(Saros 130)
December 13, 1936
(Saros 131)
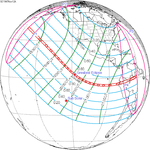November 12, 1947
(Saros 132)
October 12, 1958
(Saros 133)

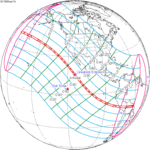September 11, 1969
(Saros 134)
August 10, 1980
(Saros 135)
July 11, 1991
(Saros 136)
June 10, 2002
(Saros 137)
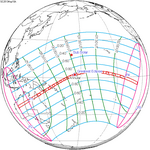May 10, 2013
(Saros 138)

April 8, 2024
(Saros 139)
March 9, 2035
(Saros 140)
February 5, 2046
(Saros 141)
January 5, 2057
(Saros 142)
December 6, 2067
(Saros 143)

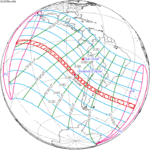November 4, 2078
(Saros 144)
October 4, 2089
(Saros 145)
September 4, 2100
(Saros 146)
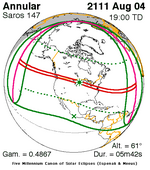August 4, 2111
(Saros 147)
July 4, 2122
(Saros 148)

June 3, 2133
(Saros 149)
May 3, 2144
(Saros 150)
April 2, 2155
(Saros 151)
March 2, 2166
(Saros 152)
January 29, 2177
(Saros 153)

December 29, 2187
(Saros 154)
November 28, 2198
(Saros 155)

Example lunar Tritos series

The tritos series repeats 31 days short of 11 years at alternating nodes. Sequential events have incremental Saros cycle indices.

This series produces 23 total eclipses between June 22, 1880 and August 9, 2120.

Tritos eclipse series (subset 1901–2100)
Ascending node   Descending node
Saros Date
Viewing 		Type
chart 		Saros Date
Viewing 		Type
chart
120 1902 Apr 22
 Total
 121 1913 Mar 22
 Total
122 1924 Feb 20
 Total
 123 1935 Jan 19
 Total
124 1945 Dec 19
 Total
 125 1956 Nov 18
 Total
126 1967 Oct 18
 Total
 127 1978 Sep 16
 Total
128 1989 Aug 17
 Total
 129 2000 Jul 16
 Total
130 2011 Jun 15
 Total
 131 2022 May 16
 Total
132 2033 Apr 14
 Total
 133 2044 Mar 13
 Total
134 2055 Feb 11
 Total
 135 2066 Jan 11
 Total
136 2076 Dec 10
 Total
 137 2087 Nov 10
 Total
138 2098 Oct 10
 Total

See also

References

  • Mathematical Astronomy Morsels, Jean Meeus, Willmann-Bell, Inc., 1997 (Chapter 9, p. 51, Table 9.A Some eclipse Periodicities)
Category: