| Truncated tetrakis cube Hexatruncated tetrakis cube | |
|---|---|
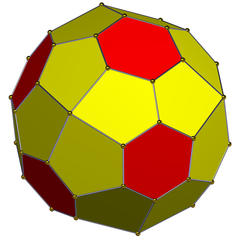
| |
| Conway notation | t6kC = dk6tO |
| Faces | 8 hexagons 24 pentagons |
| Edges | 84 |
| Vertices | 54 |
| Dual | Hexakis truncated octahedron |
| Vertex configuration | 6 (5.5.5.5) 48 (5.5.6) |
| Symmetry group | Oh |
| Properties | convex |
The truncated tetrakis cube, or more precisely an order-6 truncated tetrakis cube or hexatruncated tetrakis cube, is a convex polyhedron with 32 faces: 24 sets of 3 bilateral symmetry pentagons arranged in an octahedral arrangement, with 8 regular hexagons in the gaps.
Construction
It is constructed from a tetrakis cube by truncating the order-6 vertices. This creates 4 regular hexagon faces, and leaves 12 mirror-symmetric pentagons.
 tetrakis cube |
Hexakis truncated octahedron
The dual of the order-6 truncated triakis tetrahedron is called a hexakis truncated octahedron. It is constructed by a truncated octahedron with hexagonal pyramids augmented.
 Truncated octahedron |
 hexakis truncated octahedron |
See also
External links
This polyhedron-related article is a stub. You can help Misplaced Pages by expanding it. |