Two-cube calendar - Misplaced Pages

Mechanical device which calculates the day of "any" provided date

	Tu			0			0
W	Th	F	8	7	6	5	4	3
	Sa			1			1
	Su			2			2

	f			l			g
v	a	c	t	u	b	j	o	y
	n			m			r
	s			p			e

One possible set of nets for the cubes (6 doubling as 9, n as u, p as d, and W as M)

A two-cube calendar is a desk calendar consisting of two cubes with faces marked by digits 0 through 9. Each face of each cube is marked with a single digit, and it is possible to arrange the cubes so that any chosen day of the month (from 01, 02, ... through 31) is visible on the two front faces.

A puzzle about the two-cube calendar was described in Gardner's column in Scientific American. In the puzzle discussed in Mathematical Circus (1992), two visible faces of one cube have digits 1 and 2 on them, and three visible faces of another cube have digits 3, 4, 5 on them. The cubes are arranged so that their front faces indicate the 25th day of the current month. The problem is to determine the digits hidden on the seven invisible faces.

Gardner wrote he saw a two-cube desk calendar in a store window in New York. According to a letter received by Gardner from John S. Singleton (England), Singleton patented the calendar in 1957, but the patent lapsed in 1965.

A number of variations are manufactured and sold as souvenirs, differing in the appearance and the existence of additional bars or cubes to set the current month and the day of week.

Solution of the problem

Digits 1 and 2 need to be placed on both cubes to allow numbers 11 and 22. That leaves us with 4 sides of each cube (total of 8) for another 8 digits. However, digit 0 needs to be combined with all other digits, so it also needs to be placed on both cubes. That means we need to place remaining 7 digits (from 3 to 9) on the remaining 6 sides of cubes. The solution is possible because digit 6 looks like inverted 9.

Therefore, the solution of the problem is:

${\begin{cases}C_{1}:=\{0,1,2,3,4,5\}\\C_{2}:=\{0,1,2,{\tfrac {6}{9}},7,8\}\\\end{cases}}$

If the problem is based on another given set of visible digits, the last three digits of each cube could be shuffled between the cubes.

Three-cube variation for the month abbreviations

A variation with three cubes providing English abbreviations for the twelve months is discussed in a Scientific American column in December 1977. One solution of this variation allows displaying the first three letters of any month and relies on the fact that lower-case letters u and n and also p and d are inverses of each other.

${\begin{cases}C_{1}:=\{e,g,j,o,r,y\}\\C_{2}:=\{a,c,f,{\tfrac {n}{u}},s,v\}\\C_{3}:=\{b,{\tfrac {d}{p}},l,m,{\tfrac {u}{n}},t\}\\\end{cases}}$

Polish 3-letter month abbreviations (informal but commonly used for date rubber stamps - sty, lut, mar, kwi, maj, cze, lip, sie, wrz, paź, lis, gru) are also feasible, both in lower and upper case:

${\begin{cases}C_{1}:=\{a,e,g,l,w,y\}\\C_{2}:=\{c,i,j,r,t,{\acute {z}}\}\\C_{3}:=\{k,m,p,s,u,z\}\\\end{cases}}$

Four-cube variation

Using four cubes for two-digit day number from 01 to 31 and two-digit month number from 01 to 12, and assuming that digits 6 and 9 are indistinguishable, it is possible to represent all days of the year. One possible solution is:

${\begin{cases}C_{1}:=\{0,1,X,3,4,5\}\\C_{2}:=\{0,1,2,3,4,5\}\\C_{3}:=\{0,1,2,{\tfrac {6}{9}},7,8\}\\C_{4}:=\{0,1,2,{\tfrac {6}{9}},7,8\}\\\end{cases}}$

The $X$ could be any digit. The last three digits of each cube could be shuffled between the cubes such that each digit from 3 to 9 is placed on at least two different cubes.

With assumption that 6 and 9 are distinguishable characters, it is impossible to represent all days of the year because the necessary number of faces would be 25 and four cubes have only 24 faces. However, it is possible to represent almost all days in the year. There is a family of the best solutions which excludes only one day, namely Nov 11, e.g.:

${\begin{cases}C_{1}:=\{0,2,3,4,5,6\}\\C_{2}:=\{0,1,3,4,5,6\}\\C_{3}:=\{0,1,2,7,8,9\}\\C_{4}:=\{0,1,2,7,8,9\}\\\end{cases}}$

The last four digits of each cube could be shuffled between the cubes such that no cube has two identical faces (especially the 2's).

Four-cube variation for weekday-day-month-year display

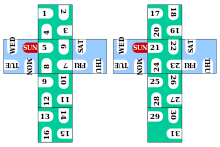
Maintaining the condition that four visible faces of four cubes should combine to display any possible combination of weekday-day-month-year clearly, the 6 faces of each cube are divided in 4 quarters each to have 24 spaces (ie 6*4) on each cube (a total of 96 spaces) for writing the weekday (Sun, Mon, Tues, Wed, Thurs, Fri and Sat), the day (1 to 31: days of the month), the month (Jan, Feb, Mar, Apr, May, Jun, Jul, Aug, Sep, Oct, Nov and Dec), and the year (N to N+23; N being replaced by any year). This setup works for 24 years.

For the weekday-day-month-year format of display, the weekday and the month are written adjacent to the right edge of the cube, and the day and the year are written adjacent to the left edge of the cube in a cyclical manner, so that the four visible faces of the cubes combine to display all the possible combinations of day-date clearly and distinctly. The weekday and day can be written in any order as long as all the 7 days (Sunday through Saturday) are written on two of the four cubes and the 31 dates (1 through 31) are split in two groups of 15 and 16 numbers on the two cubes. The month and year can also be written in any order as long as all the 12 months (January through December) are written on the other two cubes and the 24 years (N through N+23) are split in two groups of 12 numbers on the two cubes.

The weekday-day and month-year parts can work independently from each other, meaning that one part can be removed without affecting the other (as shown on the picture above).

One of the possible solutions is:

${\begin{cases}C_{1}:=\{1/2/3/4,5/6/7/8,9/10/11/12,13/14/15/16,sun/mon/tue/wed,thu/fri/sat/blank\}\\C_{2}:=\{17/18/19/20,21/22/23/24,25/26/27/28,29/30/31/blank,sun/mon/tue/wed,thu/fri/sat/blank\}\\C_{3}:=\{N/N+1/N+2/N+3,N+4/N+5/N+6/N+7,N+8/N+9/N+10/N+11,jan/feb/mar/apr,may/jun/jul/aug,sep/oct/nov/dec\}\\C_{4}:=\{N+12/N+13/N+14/N+15,N+16/N+17/N+18/N+19,N+20/N+21/N+22/N+23,jan/feb/mar/apr,mau/jun/jul/aug,sep/oct/nov/dec\}\\\end{cases}}$

The original video explaining how to build the weekday-day-month-year cubes can be found on this YouTube channel

References

^ Gardner, Mathematical Circus, 1992, p. 186.
Gary Antonick (2014-10-20). "Remembering Martin Gardner". The New York Times.
"United Kingdom Patent 831572-A: Improvements in and relating to perpetual calendar device".
Gardner, Mathematical Circus, 1992, pp. 196-197.
Stewart, 2010, p. 35.
Gardner, Mathematical Circus, 1992, p. 197.
Martin Gardner (1985). The Magic Numbers of Dr. Matrix. Buffalo, N.Y.: Prometheus Books. pp. 210, 308. ISBN 0-87975-281-5. LCCN 84-43183.
"Extended Calendar Cube Question". StackExchange.
"Weekday-Day-Month-Year Display using Four Cubes, by Chandrakant Kanetkar". YouTube.

Sources

Martin Gardner (1992). Mathematical Circus. Washington, DC: MAA. pp. 186, 196–197. ISBN 0-88385-506-2. LCCN 92-060996.
Ian Stewart (2010). "Perpetual Calendar". Professor Stewart's Cabinet of Mathematical Curiosities. Profile Books. pp. 35, 260. ISBN 1847651283.

External links

Jenny Murray. "The Colossal Book of Short Puzzles and Problems: Review by Jenny Murray". Association of Teachers of Mathematics. Archived from the original on 2015-05-09.

This puzzle/logic game-related article is a stub. You can help Misplaced Pages by expanding it.

Categories: