
In radio communications, a sideband is a band of frequencies higher than or lower than the carrier frequency, that are the result of the modulation process. The sidebands carry the information transmitted by the radio signal. The sidebands comprise all the spectral components of the modulated signal except the carrier. The signal components above the carrier frequency constitute the upper sideband (USB), and those below the carrier frequency constitute the lower sideband (LSB). All forms of modulation produce sidebands.
Sideband creation
We can illustrate the creation of sidebands with one trigonometric identity:
Adding to both sides:
Substituting (for instance) and where represents time:
Adding more complexity and time-variation to the amplitude modulation also adds it to the sidebands, causing them to widen in bandwidth and change with time. In effect, the sidebands "carry" the information content of the signal.
Sideband Characterization
In the example above, a cross-correlation of the modulated signal with a pure sinusoid, is zero at all values of except 1100, 1000, and 900. And the non-zero values reflect the relative strengths of the three components. A graph of that concept, called a Fourier transform (or spectrum), is the customary way of visualizing sidebands and defining their parameters.
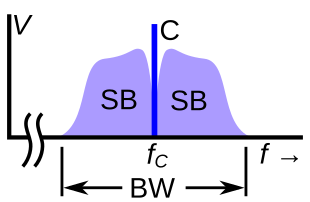
Amplitude modulation
Amplitude modulation of a carrier signal normally results in two mirror-image sidebands. The signal components above the carrier frequency constitute the upper sideband (USB), and those below the carrier frequency constitute the lower sideband (LSB). For example, if a 900 kHz carrier is amplitude modulated by a 1 kHz audio signal, there will be components at 899 kHz and 901 kHz as well as 900 kHz in the generated radio frequency spectrum; so an audio bandwidth of (say) 7 kHz will require a radio spectrum bandwidth of 14 kHz. In conventional AM transmission, as used by broadcast band AM stations, the original audio signal can be recovered ("detected") by either synchronous detector circuits or by simple envelope detectors because the carrier and both sidebands are present. This is sometimes called double sideband amplitude modulation (DSB-AM), but not all variants of DSB are compatible with envelope detectors.
In some forms of AM, the carrier may be reduced, to save power. The term DSB reduced-carrier normally implies enough carrier remains in the transmission to enable a receiver circuit to regenerate a strong carrier or at least synchronise a phase-locked loop but there are forms where the carrier is removed completely, producing double sideband with suppressed carrier (DSB-SC). Suppressed carrier systems require more sophisticated circuits in the receiver and some other method of deducing the original carrier frequency. An example is the stereophonic difference (L-R) information transmitted in stereo FM broadcasting on a 38 kHz subcarrier where a low-power signal at half the 38-kHz carrier frequency is inserted between the monaural signal frequencies (up to 15 kHz) and the bottom of the stereo information sub-carrier (down to 38–15 kHz, i.e. 23 kHz). The receiver locally regenerates the subcarrier by doubling a special 19 kHz pilot tone. In another example, the quadrature modulation used historically for chroma information in PAL television broadcasts, the synchronising signal is a short burst of a few cycles of carrier during the "back porch" part of each scan line when no image is transmitted. But in other DSB-SC systems, the carrier may be regenerated directly from the sidebands by a Costas loop or squaring loop. This is common in digital transmission systems such as BPSK where the signal is continually present.
If part of one sideband and all of the other remain, it is called vestigial sideband, used mostly with television broadcasting, which would otherwise take up an unacceptable amount of bandwidth. Transmission in which only one sideband is transmitted is called single-sideband modulation or SSB. SSB is the predominant voice mode on shortwave radio other than shortwave broadcasting. Since the sidebands are mirror images, which sideband is used is a matter of convention.
In SSB, the carrier is suppressed, significantly reducing the electrical power (by up to 12 dB) without affecting the information in the sideband. This makes for more efficient use of transmitter power and RF bandwidth, but a beat frequency oscillator must be used at the receiver to reconstitute the carrier. If the reconstituted carrier frequency is wrong then the output of the receiver will have the wrong frequencies, but for speech small frequency errors are no problem for intelligibility. Another way to look at an SSB receiver is as an RF-to-audio frequency transposer: in USB mode, the dial frequency is subtracted from each radio frequency component to produce a corresponding audio component, while in LSB mode each incoming radio frequency component is subtracted from the dial frequency.
Frequency modulation
Frequency modulation also generates sidebands, the bandwidth consumed depending on the modulation index - often requiring significantly more bandwidth than DSB. Bessel functions can be used to calculate the bandwidth requirements of FM transmissions. Carson's rule is a useful approximation of bandwidth in several applications.
Effects
Sidebands can interfere with adjacent channels. The part of the sideband that would overlap the neighboring channel must be suppressed by filters, before or after modulation (often both). In broadcast band frequency modulation (FM), subcarriers above 75 kHz are limited to a small percentage of modulation and are prohibited above 99 kHz altogether to protect the ±75 kHz normal deviation and ±100 kHz channel boundaries. Amateur radio and public service FM transmitters generally utilize ±5 kHz deviation.
To accurately reproduce the modulating waveform, the entire signal processing path of the system of transmitter, propagation path, and receiver must have enough bandwidth so that enough of the sidebands can be used to recreate the modulated signal to the desired degree of accuracy.
In a non-linear system such as an amplifier, sidebands of the original signal frequency components may be generated due to distortion. This is generally minimized but may be intentionally done for the fuzzbox musical effect.
See also
- Independent sideband
- Out-of-band communications involve a channel other than the main communication channel.
- Side lobe
- Sideband computing is a distributed computing method using a channel separate from the main communication channel.
- TV transmitter
References
- Tony Dorbuck (ed.), The Radio Amateur's Handbook, Fifty-Fifth Edition, American Radio Relay League, 1977, p. 368
 This article incorporates public domain material from Federal Standard 1037C. General Services Administration. Archived from the original on 2022-01-22. (in support of MIL-STD-188).
This article incorporates public domain material from Federal Standard 1037C. General Services Administration. Archived from the original on 2022-01-22. (in support of MIL-STD-188).- Department of The Army Technical Manual TM 11-685 "Fundamentals of Single Sideband Communications"

 to both sides:
to both sides:

 and
and  where
where  represents time:
represents time:

 is zero at all values of
is zero at all values of  except 1100, 1000, and 900. And the non-zero values reflect the relative strengths of the three components. A graph of that concept, called a
except 1100, 1000, and 900. And the non-zero values reflect the relative strengths of the three components. A graph of that concept, called a