
Lightness is a visual perception of the luminance of an object. It is often judged relative to a similarly lit object. In colorimetry and color appearance models, lightness is a prediction of how an illuminated color will appear to a standard observer. While luminance is a linear measurement of light, lightness is a linear prediction of the human perception of that light.
This distinction is meaningful because human vision's lightness perception is non-linear relative to light. Doubling the quantity of light does not result in a doubling in perceived lightness, only a modest increase.
The symbol for perceptual lightness is usually either as used in CIECAM02 or as used in CIELAB and CIELUV. ("Lstar") is not to be confused with as used for luminance. In some color ordering systems such as Munsell, Lightness is referenced as value.
Chiaroscuro and tenebrism both take advantage of dramatic contrasts of value to heighten drama in art. Artists may also employ shading, subtle manipulation of value.
Lightness in different colorspaces
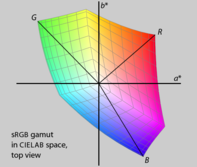 Fig 2a. The sRGB gamut mapped in CIELAB space. Notice that the lines pointing to the red, green, and blue primaries are not evenly spaced by hue angle, and are of unequal length. The primaries also have different L* values.
Fig 2a. The sRGB gamut mapped in CIELAB space. Notice that the lines pointing to the red, green, and blue primaries are not evenly spaced by hue angle, and are of unequal length. The primaries also have different L* values.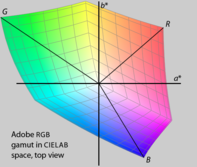 Fig 2b. The Adobe RGB gamut mapped in CIELAB space. Also notice that these two RGB spaces have different gamuts, and thus will have different HSL and HSV representations.
Fig 2b. The Adobe RGB gamut mapped in CIELAB space. Also notice that these two RGB spaces have different gamuts, and thus will have different HSL and HSV representations.
In some colorspaces or color systems such as Munsell, HCL, and CIELAB, the lightness (value) achromatically constrains the maximum and minimum limits, and operates independently of the hue and chroma. For example Munsell value 0 is pure black, and value 10 is pure white. Colors with a discernible hue must therefore have values in between these extremes.
In a subtractive color model (e.g. paint, dye, or ink) lightness changes to a color through various tints, shades, or tones can be achieved by adding white, black, or grey respectively. This also reduces saturation.
In HSL and HSV, the displayed luminance is relative to the hue and chroma for a given lightness value, in other words the selected lightness value does not predict the actual displayed luminance nor the perception thereof. Both systems use coordinate triples, where many triples can map onto the same color.
In HSV, all triples with value 0 are pure black. If the hue and saturation are held constant, then increasing the value increases the luminance, such that a value of 1 is the lightest color with the given hue and saturation. HSL is similar, except that all triples with lightness 1 are pure white. In both models, all pure saturated colors indicate the same lightness or value, but this does not relate to the displayed luminance which is determined by the hue. I.e. yellow is higher luminance than blue, even if the lightness value is set at a given number.
While HSL, HSV, and similar spaces serve well enough to choose or adjust a single color, they are not perceptually uniform. They trade off accuracy for computational simplicity, as they were created in an era where computer technology was restricted in performance.
If we take an image and extract the hue, saturation, and lightness or value components for a given color space, we will see that they may differ substantially from a different color space or model. For example, examine the following images of a fire breather (fig. 1). The original is in the sRGB color space. CIELAB is a perceptually uniform lightness prediction that is derived from luminance , but discards the and , of the CIE XYZ color space. Notice this appears similar in perceived lightness to the original color image. Luma is a gamma-encoded luminance component of some video encoding systems such as and . It is roughly similar, but differs at high chroma, deviating most from an achromatic signal such as linear luminance or non-linear lightness . HSL and HSV are neither perceptually uniform, nor uniform as to luminance.
 Fig. 1a. Color photograph (sRGB color space).
Fig. 1a. Color photograph (sRGB color space). Fig. 1b. CIELAB L* (further transformed back to sRGB for consistent display).
Fig. 1b. CIELAB L* (further transformed back to sRGB for consistent display). Fig. 1c. Rec. 601 luma Y′.
Fig. 1c. Rec. 601 luma Y′.
 Fig. 1d. Component average: "intensity" I.
Fig. 1d. Component average: "intensity" I. Fig. 1e. HSV value V.
Fig. 1e. HSV value V. Fig. 1f. HSL lightness L.
Fig. 1f. HSL lightness L.
Relationship to value and relative luminance
The Munsell value has long been used as a perceptually uniform lightness scale. A question of interest is the relationship between the Munsell value scale and the relative luminance. Aware of the Weber–Fechner law, Albert Munsell remarked "Should we use a logarithmic curve or curve of squares?" Neither option turned out to be quite correct; scientists eventually converged on a roughly cube-root curve, consistent with the Stevens's power law for brightness perception, reflecting the fact that lightness is proportional to the number of nerve impulses per nerve fiber per unit time. The remainder of this section is a chronology of lightness models, leading to CIECAM02.
Note. – Munsell's V runs from 0 to 10, while Y typically runs from 0 to 100 (often interpreted as a percentage). Typically, the relative luminance is normalized so that the "reference white" (say, magnesium oxide) has a tristimulus value of Y = 100. Since the reflectance of magnesium oxide (MgO) relative to the perfect reflecting diffuser is 97.5%, V = 10 corresponds to Y = 100/97.5% ≈ 102.6 if MgO is used as the reference.

1920
Irwin Priest, Kasson Gibson, and Harry McNicholas provide a basic estimate of the Munsell value (with Y running from 0 to 1 in this case):
1933
Alexander Munsell, Louise Sloan, and Isaac Godlove launch a study on the Munsell neutral value scale, considering several proposals relating the relative luminance to the Munsell value, and suggest:
1943
Sidney Newhall, Dorothy Nickerson, and Deane Judd prepare a report for the Optical Society of America (OSA) on Munsell renotation. They suggest a quintic parabola (relating the reflectance in terms of the value):
1943
Using Table II of the OSA report, Parry Moon and Domina Spencer express the value in terms of the relative luminance:
1944
Jason Saunderson and B.I. Milner introduce a subtractive constant in the previous expression, for a better fit to the Munsell value. Later, Dorothea Jameson and Leo Hurvich claim that this corrects for simultaneous contrast effects.
1955
Ladd and Pinney of Eastman Kodak are interested in the Munsell value as a perceptually uniform lightness scale for use in television. After considering one logarithmic and five power-law functions (per Stevens' power law), they relate value to reflectance by raising the reflectance to the power of 0.352:
Realizing this is quite close to the cube root, they simplify it to:
1958
Glasser et al. define the lightness as ten times the Munsell value (so that the lightness ranges from 0 to 100):
1964
Günter Wyszecki simplifies this to:
This formula approximates the Munsell value function for 1% < Y < 98% (it is not applicable for Y < 1%) and is used for the CIE 1964 color space.
1976
CIELAB uses the following formula:
where Yn is the CIE XYZ Y tristimulus value of the reference white point (the subscript n suggests "normalized") and is subject to the restriction Y/Yn > 0.01. Pauli removes this restriction by computing a linear extrapolation which maps Y/Yn = 0 to L* = 0 and is tangent to the formula above at the point at which the linear extension takes effect. First, the transition point is determined to be Y/Yn = (6/29) ≈ 0.008856, then the slope of (29/3) ≈ 903.3 is computed. This gives the two-part function:
The lightness is then:
At first glance, you might approximate the lightness function by a cube root, an approximation that is found in much of the technical literature. However, the linear segment near black is significant, and so the 116 and 16 coefficients. The best-fit pure power function has an exponent of about 0.42, far from 1/3. An approximately 18% grey card, having an exact reflectance of (33/58), has a lightness value of 50. It is called "mid grey" because its lightness is midway between black and white.
1997
As early as in 1967 a hyperbolic relationship between light intensity and cone cell responses was discovered in fish, in line with the Michaelis–Menten kinetics model of biochemical reactions. In the 70s the same relationship was found in a number of other vertebrates and in 1982, using microelectrodes to measure cone responses in living rhesus macaques, Valeton and Van Norren found the following relationship:
- 1 / V ~ 1 + (σ / I)
where V is the measured potential, I the light intensity and σ a constant. In 1986 Seim and Valberg realised that this relationship might aid in the construction of a more uniform colour space. This inspired advances in colour modelling and when the International Commission on Illumination held a symposium in 1996, objectives for a new standard colour model were formulated and in 1997 CIECAM97s (International Commission on Illumination, colour appearance model, 1997, simple version) was standardised. CIECAM97s distinguishes between lightness, how light something appears compared to a similarly lit white object, and brightness, how much light appears to shine from something. According to CIECAM97s the lightness of a sample is:
- J = 100 (Asample / Awhite)
In this formula, for a small sample under bright conditions in a surrounding field with a relative luminance n compared to white, c has been chosen such that:
This models that a sample will appear darker on a light background than on a dark background. See contrast effect for more information on the topic. When n = 1/5, cz = 1, representing the assumption that most scenes have an average relative luminance of 1/5 compared to bright white, and that therefore a sample in such a surround should be perceived at its proper lightness. The quantity A models the achromatic cone response; it is colour dependent but for a grey sample under bright conditions it works out as:
- Nbb is a fudge factor that is normally 1; it's only of concern when comparing brightness judgements based on slightly different reference whites.
Here Y is the relative luminance compared to white on a scale of 0 to 1 and LA is the average luminance of the adapting visual field as a whole, measured in cd/m. The achromatic response follows a kind of S-curve, ranging from 1 to 123, numbers which follow from the way the cone responses are averaged and which are ultimately based on a rough estimate for the useful range of nerve impulses per second, and which has a fairly large intermediate range where it roughly follows a square root curve. The brightness according to CIECAM97s is then:
- Q = (1.24 / c) (J / 100) (Awhite + 3)
The factor 1.24 / c is a surround factor that reflects that scenes appear brighter in dark surrounding conditions. Suggestions for a more comprehensive model, CIECAM97C, were also formulated, to take into account several effects at extremely dark or bright conditions, coloured lighting, as well as the Helmholtz–Kohlrausch effect, where highly chromatic samples appear lighter and brighter in comparison to a neutral grey. To model the latter effect, in CIECAM97C the formula for J is adjusted as follows:
- JHK = J + (100 – J) (C / 300) |sin(1/2h – 45°)|,
where C is the chroma and h the hue angle
Q is then calculated from JHK instead of from J. This formula has the effect of pulling up the lightness and brightness of coloured samples. The larger the chroma, the stronger the effect; for very saturated colours C can be close to 100 or even higher. The absolute sine term has a sharp V-shaped valley with a zero at yellow and a broad plateau in the deep blues.
2002
The achromatic response in CIECAM97s is a weighted addition of cone responses minus 2.05. Since the total noise term adds up to 3.05, this means that A and consequentially J and Q aren't zero for absolute black. To fix this, Li, Luo & Hunt suggested subtracting 3.05 instead, so the scale starts at zero. Although CIECAM97s was a successful model to spur and direct colorimetric research, Fairchild felt that for practical applications some changes were necessary. Those relevant for lightness calculations were to, rather than use several discrete values for the surround factor c, allow for linear interpolation of c and thereby allowing the model to be used under intermediate surround conditions, and to simplify z to remove the special case for large stimuli because he felt it was irrelevant for imaging applications. Based on experimental results, Hunt, Li, Juan and Luo proposed a number of improvements. Relevant for the topic at hand is that they suggested lowering z slightly. Li and Luo found that a colour space based on such a modified CIECAM97s using lightness as one of the coordinates was more perceptually uniform than CIELAB.
Because of the shape of the cone response S-curve, when the luminance of a colour is reduced, even if its spectral composition remains the same, the different cone responses do not quite change at the same rate with respect to each other. It is plausible therefore that the perceived hue and saturation will change at low luminance levels. But CIECAM97s predicts much larger deviations than are generally thought likely and therefore Hunt, Li and Luo suggested using a cone response curve which approximates a power curve for a much larger range of stimuli, so hue and saturation are better preserved.
All these proposals, as well as others relating to chromaticity, resulted in a new colour appearance model, CIECAM02. In this model, the formula for lightness remains the same:
- J = 100 (Asample / Awhite)
But all the quantities that feed into this formula change in some way. The parameter c is now continuously variable as discussed above and z = 1.48 + √n. Although this is higher than z in CIECAM97s, the total effective power factor is very similar because the effective power factor of the achromatic response is much lower:
As before, this formula assumes bright conditions. Apart from 1220, which results from an arbitrarily assumed cone response constant, the various constants in CIECAM02 were fitted to experimental data sets. The expression for the brightness has also changed considerably:
Note that contrary to the suggestion from CIECAM97C, CIECAM02 contains no provision for the Helmholtz–Kohlrausch effect.
Other psychological effects
This subjective perception of luminance in a non-linear fashion is one thing that makes gamma compression of images worthwhile. Beside this phenomenon there are other effects involving perception of lightness. Chromaticity can affect perceived lightness as described by the Helmholtz–Kohlrausch effect. Though the CIELAB space and relatives do not account for this effect on lightness, it may be implied in the Munsell color model. Light levels may also affect perceived chromaticity, as with the Purkinje effect.
See also
References
- Most of the disadvantages below are listed in A Technical Introduction to Digital Video (1996) by Charles Poynton, though as mere statements, without examples.
- Kuehni, Rolf G. (February 2002). "The early development of the Munsell system". Color Research & Application. 27 (1): 20–27. doi:10.1002/col.10002.
- Hunt, Robert W. G. (May 18, 1957). "Light Energy and Brightness Sensation". Nature. 179 (4568): 1026. Bibcode:1957Natur.179Q1026H. doi:10.1038/1791026a0. PMID 13430776.
- Valberg, Arne (2006). Light Vision Color. John Wiley and Sons. p. 200. ISBN 978-0470849026.
- Priest, Irwin G.; Gibson, K.S.; McNicholas, H.J. (September 1920). "An examination of the Munsell color system. I: Spectral and total reflection and the Munsell scale of Value". Technical Paper 167 (3). United States Bureau of Standards: 27.
- Munsell, A.E.O.; Sloan, L.L.; Godlove, I.H. (November 1933). "Neutral value scales. I. Munsell neutral value scale". JOSA. 23 (11): 394–411. Bibcode:1933JOSA...23..394M. doi:10.1364/JOSA.23.000394. Note: This paper contains a historical survey stretching to 1760.
- Munsell, A.E.O.; Sloan, L.L.; Godlove, I.H. (December 1933). "Neutral value scales. II. A comparison of results and equations describing value scales". JOSA. 23 (12): 419–425. Bibcode:1933JOSA...23..419G. doi:10.1364/JOSA.23.000419.
- Newhall, Sidney M.; Nickerson, Dorothy; Judd, Deane B (May 1943). "Final report of the O.S.A. subcommittee on the spacing of the Munsell colors". Journal of the Optical Society of America. 33 (7): 385–418. Bibcode:1943JOSA...33..385N. doi:10.1364/JOSA.33.000385.
- Moon, Parry; Spencer, Domina Eberle (May 1943). "Metric based on the composite color stimulus". JOSA. 33 (5): 270–277. Bibcode:1943JOSA...33..270M. doi:10.1364/JOSA.33.000270.
- Saunderson, Jason L.; Milner, B.I. (March 1944). "Further study of ω space". JOSA. 34 (3): 167–173. Bibcode:1944JOSA...34..167S. doi:10.1364/JOSA.34.000167.
- Hurvich, Leo M.; Jameson, Dorothea (November 1957). "An Opponent-Process Theory of Color Vision". Psychological Review. 64 (6): 384–404. doi:10.1037/h0041403. PMID 13505974. S2CID 27613265.
- Jameson, Dorothea; Leo M. Hurvich (May 1964). "Theory of brightness and color contrast in human vision". Vision Research. 4 (1–2): 135–154. doi:10.1016/0042-6989(64)90037-9. PMID 5888593.
- Ladd, J.H.; Pinney, J.E. (September 1955). "Empirical relationships with the Munsell Value scale". Proceedings of the Institute of Radio Engineers. 43 (9): 1137. doi:10.1109/JRPROC.1955.277892.
- Glasser, L.G.; A.H. McKinney; C.D. Reilly; P.D. Schnelle (October 1958). "Cube-root color coordinate system". JOSA. 48 (10): 736–740. Bibcode:1958JOSA...48..736G. doi:10.1364/JOSA.48.000736.
- Wyszecki, Günter (November 1963). "Proposal for a New Color-Difference Formula". JOSA. 53 (11): 1318–1319. Bibcode:1963JOSA...53.1318W. doi:10.1364/JOSA.53.001318. Note: The asterisks are not used in the paper.
- Pauli, Hartmut K.A. (1976). "Proposed extension of the CIE recommendation on "Uniform color spaces, color spaces, and color-difference equations, and metric color terms"". JOSA. 66 (8): 866–867. doi:10.1364/JOSA.66.000866.
- Poynton, Charles; Funt, Brian (February 2014). "Perceptual uniformity in digital image representation and display". Color Research and Application. 39 (1): 6–15. doi:10.1002/col.21768.
- Ken-Ichi Naka & William Albert Hugh Rushton: The generation and spread of S-potentials in fish (Cyprinidae)
- Jean Mathieu Valeton & Dirk van Norren: Light adaptation of primate cones: An analysis based on extracellular data
- Thorstein Seim & Arne Valberg: Towards a uniform color space: A better formula to describe the Munsell and OSA color scales
- Mark D. Fairchild: Color Appearance Models § The CIE Color Appearance Model (1997), CIECAM97s
- Robert William Gainer Hunt: Some comments on using the CIECAM97s colour-appearance model
- Ming Ronnier Luo & Robert William Gainer Hunt: The structure of the CIE 1997 colour appearance model
- Changjun Li, Ming Ronnier Luo & Robert William Gainer Hunt: A revision of the CIECAM97s model
- Mark D. Fairchild: A revision of CIECAM97s for practical applications
- Robert William Gainer Hunt, Changjun Li, Lu-Yin Grace Juan & Ming Ronnier Luo: Further improvements to CIECAM97s (also cited as Further refinements to CIECAM97s)
- Changjun Li & Ming Ronnier Luo: A uniform colour space based upon CIECAM97s
- Robert William Gainer Hunt, Changjun Li & Ming Ronnier Luo: Dynamic cone response functions for models of colour appearance
- Nathan Moroney, Mark D. Fairchild, Robert William Gainer Hunt, Changjun Li, Ming Ronnier Luo & Todd Newman: The CIECAM02 color appearance model
- CIE technical committee: Colour Appearance Models for Color Management Applications
External links
![]() Media related to Lightness at Wikimedia Commons
Media related to Lightness at Wikimedia Commons
| Color topics | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Color science |
|  | ||||||||
| Color philosophy |
| |||||||||
| Color terms |
| |||||||||
| Color organizations | ||||||||||
| Names |
| |||||||||
| Related | ||||||||||
 of an object. It is often judged relative to a similarly lit object. In
of an object. It is often judged relative to a similarly lit object. In  as used in
as used in  as used in
as used in  as used for luminance. In some color ordering systems such as
as used for luminance. In some color ordering systems such as  , but discards the
, but discards the  and
and  , of the
, of the  is a gamma-encoded luminance component of some video encoding systems such as
is a gamma-encoded luminance component of some video encoding systems such as  and
and  . It is roughly similar, but differs at high chroma, deviating most from an achromatic signal such as linear luminance
. It is roughly similar, but differs at high chroma, deviating most from an achromatic signal such as linear luminance  are neither perceptually uniform, nor uniform as to luminance.
are neither perceptually uniform, nor uniform as to luminance.















