| Relevant topics on |
| Graph connectivity |
|---|
In graph theory, a vertex subset is a vertex separator (or vertex cut, separating set) for nonadjacent vertices a and b if the removal of S from the graph separates a and b into distinct connected components.
Examples
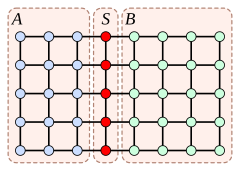
Consider a grid graph with r rows and c columns; the total number n of vertices is r × c. For instance, in the illustration, r = 5, c = 8, and n = 40. If r is odd, there is a single central row, and otherwise there are two rows equally close to the center; similarly, if c is odd, there is a single central column, and otherwise there are two columns equally close to the center. Choosing S to be any of these central rows or columns, and removing S from the graph, partitions the graph into two smaller connected subgraphs A and B, each of which has at most n⁄2 vertices. If r ≤ c (as in the illustration), then choosing a central column will give a separator S with vertices, and similarly if c ≤ r then choosing a central row will give a separator with at most vertices. Thus, every grid graph has a separator S of size at most the removal of which partitions it into two connected components, each of size at most n⁄2.
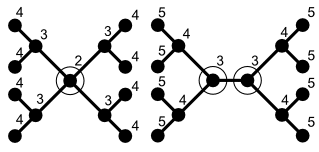
To give another class of examples, every free tree T has a separator S consisting of a single vertex, the removal of which partitions T into two or more connected components, each of size at most n⁄2. More precisely, there is always exactly one or exactly two vertices, which amount to such a separator, depending on whether the tree is centered or bicentered.
As opposed to these examples, not all vertex separators are balanced, but that property is most useful for applications in computer science, such as the planar separator theorem.
Minimal separators
Let S be an (a,b)-separator, that is, a vertex subset that separates two nonadjacent vertices a and b. Then S is a minimal (a,b)-separator if no proper subset of S separates a and b. More generally, S is called a minimal separator if it is a minimal separator for some pair (a,b) of nonadjacent vertices. Notice that this is different from minimal separating set which says that no proper subset of S is a minimal (u,v)-separator for any pair of vertices (u,v). The following is a well-known result characterizing the minimal separators:
Lemma. A vertex separator S in G is minimal if and only if the graph G – S, obtained by removing S from G, has two connected components C1 and C2 such that each vertex in S is both adjacent to some vertex in C1 and to some vertex in C2.
The minimal (a,b)-separators also form an algebraic structure: For two fixed vertices a and b of a given graph G, an (a,b)-separator S can be regarded as a predecessor of another (a,b)-separator T, if every path from a to b meets S before it meets T. More rigorously, the predecessor relation is defined as follows: Let S and T be two (a,b)-separators in G. Then S is a predecessor of T, in symbols , if for each x ∈ S \ T, every path connecting x to b meets T. It follows from the definition that the predecessor relation yields a preorder on the set of all (a,b)-separators. Furthermore, Escalante (1972) proved that the predecessor relation gives rise to a complete lattice when restricted to the set of minimal (a,b)-separators in G.
See also
- Chordal graph, a graph in which every minimal separator is a clique.
- k-vertex-connected graph
Notes
- George (1973). Instead of using a row or column of a grid graph, George partitions the graph into four pieces by using the union of a row and a column as a separator.
- Jordan (1869)
- Golumbic (1980).
References
- Escalante, F. (1972). "Schnittverbände in Graphen". Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg. 38: 199–220. doi:10.1007/BF02996932.
- George, J. Alan (1973), "Nested dissection of a regular finite element mesh", SIAM Journal on Numerical Analysis, 10 (2): 345–363, Bibcode:1973SJNA...10..345G, doi:10.1137/0710032, JSTOR 2156361.
- Golumbic, Martin Charles (1980), Algorithmic Graph Theory and Perfect Graphs, Academic Press, ISBN 0-12-289260-7.
- Jordan, Camille (1869). "Sur les assemblages de lignes". Journal für die reine und angewandte Mathematik (in French). 70 (2): 185–190.
- Rosenberg, Arnold; Heath, Lenwood (2002). Graph Separators, with Applications. Frontiers of Computer Science. Springer. doi:10.1007/b115747. ISBN 0-306-46464-0.
 is a vertex separator (or vertex cut, separating set) for nonadjacent
is a vertex separator (or vertex cut, separating set) for nonadjacent  vertices, and similarly if c ≤ r then choosing a central row will give a separator with at most
vertices, and similarly if c ≤ r then choosing a central row will give a separator with at most  vertices. Thus, every grid graph has a separator S of size at most
vertices. Thus, every grid graph has a separator S of size at most  the removal of which partitions it into two connected components, each of size at most n⁄2.
the removal of which partitions it into two connected components, each of size at most n⁄2.
 , if for each x ∈ S \ T, every path connecting x to b meets T. It follows from the definition that the predecessor relation yields a
, if for each x ∈ S \ T, every path connecting x to b meets T. It follows from the definition that the predecessor relation yields a