Misplaced Pages

Viterbi decoder

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
(Redirected from Viterbi decoding) Decodes a bitstream with the Viterbi algorithm

A Viterbi decoder uses the Viterbi algorithm for decoding a bitstream that has been encoded using a convolutional code or trellis code.

There are other algorithms for decoding a convolutionally encoded stream (for example, the Fano algorithm). The Viterbi algorithm is the most resource-consuming, but it does the maximum likelihood decoding. It is most often used for decoding convolutional codes with constraint lengths k≤3, but values up to k=15 are used in practice.

Viterbi decoding was developed by Andrew J. Viterbi and published in the paper Viterbi, A. (April 1967). "Error Bounds for Convolutional Codes and an Asymptotically Optimum Decoding Algorithm". IEEE Transactions on Information Theory. 13 (2): 260–269. doi:10.1109/tit.1967.1054010.

There are both hardware (in modems) and software implementations of a Viterbi decoder.

Viterbi decoding is used in the iterative Viterbi decoding algorithm.

Hardware implementation

A common way to implement a hardware viterbi decoder

A hardware Viterbi decoder for basic (not punctured) code usually consists of the following major blocks:

  • Branch metric unit (BMU)
  • Path metric unit (PMU)
  • Traceback unit (TBU)

Branch metric unit (BMU)

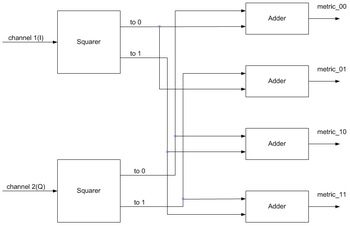
A sample implementation of a branch metric unit

A branch metric unit's function is to calculate branch metrics, which are normed distances between every possible symbol in the code alphabet, and the received symbol.

There are hard decision and soft decision Viterbi decoders. A hard decision Viterbi decoder receives a simple bitstream on its input, and a Hamming distance is used as a metric. A soft decision Viterbi decoder receives a bitstream containing information about the reliability of each received symbol. For instance, in a 3-bit encoding, this reliability information can be encoded as follows:

value meaning
000 strongest 0
001 relatively strong 0
010 relatively weak 0
011 weakest 0
100 weakest 1
101 relatively weak 1
110 relatively strong 1
111 strongest 1

Of course, it is not the only way to encode reliability data.

The squared Euclidean distance is used as a metric for soft decision decoders.

Path metric unit (PMU)

A sample implementation of a path metric unit for a specific K=4 decoder

A path metric unit summarizes branch metrics to get metrics for 2 K − 1 {\displaystyle 2^{K-1}} paths, where K is the constraint length of the code, one of which can eventually be chosen as optimal. Every clock it makes 2 K − 1 {\displaystyle 2^{K-1}} decisions, throwing off wittingly nonoptimal paths. The results of these decisions are written to the memory of a traceback unit.

The core elements of a PMU are ACS (Add-Compare-Select) units. The way in which they are connected between themselves is defined by a specific code's trellis diagram.

Since branch metrics are always ≥ 0 {\displaystyle \geq 0} , there must be an additional circuit (not shown on the image) preventing metric counters from overflow. An alternate method that eliminates the need to monitor the path metric growth is to allow the path metrics to "roll over"; to use this method it is necessary to make sure the path metric accumulators contain enough bits to prevent the "best" and "worst" values from coming within 2 of each other. The compare circuit is essentially unchanged.

A sample implementation of an ACS unit

It is possible to monitor the noise level on the incoming bit stream by monitoring the rate of growth of the "best" path metric. A simpler way to do this is to monitor a single location or "state" and watch it pass "upward" through say four discrete levels within the range of the accumulator. As it passes upward through each of these thresholds, a counter is incremented that reflects the "noise" present on the incoming signal.

Traceback unit (TBU)

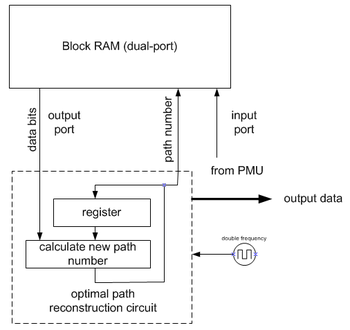
A sample implementation of a traceback unit

Back-trace unit restores an (almost) maximum-likelihood path from the decisions made by PMU. Since it does it in inverse direction, a viterbi decoder comprises a FILO (first-in-last-out) buffer to reconstruct a correct order.

Note that the implementation shown on the image requires double frequency. There are some tricks that eliminate this requirement.

Implementation issues

Quantization for soft decision decoding

In order to fully exploit benefits of soft decision decoding, one needs to quantize the input signal properly. The optimal quantization zone width is defined by the following formula:

T = N 0 2 k , {\displaystyle \,\!T={\sqrt {\frac {N_{0}}{2^{k}}}},}

where N 0 {\displaystyle N_{0}} is a noise power spectral density, and k is a number of bits for soft decision.

Euclidean metric computation

The squared norm ( ℓ 2 {\displaystyle \ell _{2}} ) distance between the received and the actual symbols in the code alphabet may be further simplified into a linear sum/difference form, which makes it less computationally intensive.

Consider a 1/2 convolutional code, which generates 2 bits (00, 01, 10 or 11) for every input bit (1 or 0). These Return-to-Zero signals are translated into a Non-Return-to-Zero form shown alongside.

code alphabet vector mapping
00 +1, +1
01 +1, −1
10 −1, +1
11 −1, −1

Each received symbol may be represented in vector form as vr = {r0, r1}, where r0 and r1 are soft decision values, whose magnitudes signify the joint reliability of the received vector, vr.

Every symbol in the code alphabet may, likewise, be represented by the vector vi = {±1, ±1}.

The actual computation of the Euclidean distance metric is:

D = ( v r → − v i → ) 2 = v r → 2 − 2 v r → v i → + v i → 2 {\displaystyle \,\!D=({\overrightarrow {v_{r}}}-{\overrightarrow {v_{i}}})^{2}={\overrightarrow {v_{r}}}^{2}-2{\overrightarrow {v_{r}}}{\overrightarrow {v_{i}}}+{\overrightarrow {v_{i}}}^{2}}

Each square term is a normed distance, depicting the energy of the symbol. For ex., the energy of the symbol vi = {±1, ±1} may be computed as

v i → 2 = ( ± 1 ) 2 + ( ± 1 ) 2 = 2 {\displaystyle \,\!{\overrightarrow {v_{i}}}^{2}=(\pm 1)^{2}+(\pm 1)^{2}=2}

Thus, the energy term of all symbols in the code alphabet is constant (at (normalized) value 2).

The Add-Compare-Select (ACS) operation compares the metric distance between the received symbol ||vr|| and any 2 symbols in the code alphabet whose paths merge at a node in the corresponding trellis, ||vi|| and ||vi||. This is equivalent to comparing

D 0 = v r → 2 − 2 v r → v i 0 → + v i 0 → 2 {\displaystyle \,\!D_{0}={\overrightarrow {v_{r}}}^{2}-2{\overrightarrow {v_{r}}}{\overrightarrow {v_{i}^{0}}}+{\overrightarrow {v_{i}^{0}}}^{2}}

and

D 1 = v r → 2 − 2 v r → v i 1 → + v i 1 → 2 {\displaystyle \,\!D_{1}={\overrightarrow {v_{r}}}^{2}-2{\overrightarrow {v_{r}}}{\overrightarrow {v_{i}^{1}}}+{\overrightarrow {v_{i}^{1}}}^{2}}

But, from above we know that the energy of vi is constant (equal to (normalized) value of 2), and the energy of vr is the same in both cases. This reduces the comparison to a minima function between the 2 (middle) dot product terms,

min ( − 2 v r → v i 0 → , − 2 v r → v i 1 → ) = max ( v r → v i 0 → , v r → v i 1 → ) {\displaystyle \,\!\min(-2{\overrightarrow {v_{r}}}{\overrightarrow {v_{i}^{0}}},-2{\overrightarrow {v_{r}}}{\overrightarrow {v_{i}^{1}}})=\max({\overrightarrow {v_{r}}}{\overrightarrow {v_{i}^{0}}},{\overrightarrow {v_{r}}}{\overrightarrow {v_{i}^{1}}})}

since a min operation on negative numbers may be interpreted as an equivalent max operation on positive quantities.

Each dot product term may be expanded as

max ( ± r 0 ± r 1 , ± r 0 ± r 1 ) {\displaystyle \,\!\max(\pm r_{0}\pm r_{1},\pm r_{0}\pm r_{1})}

where, the signs of each term depend on symbols, vi and vi, being compared. Thus, the squared Euclidean metric distance calculation to compute the branch metric may be performed with a simple add/subtract operation.

Traceback

The general approach to traceback is to accumulate path metrics for up to five times the constraint length (5 (K - 1)), find the node with the largest accumulated cost, and begin traceback from this node.

The commonly used rule of thumb of a truncation depth of five times the memory (constraint length K-1) of a convolutional code is accurate only for rate 1/2 codes. For an arbitrary rate, an accurate rule of thumb is 2.5(K - 1)/(1−r) where r is the code rate.

However, computing the node which has accumulated the largest cost (either the largest or smallest integral path metric) involves finding the maxima or minima of several (usually 2) numbers, which may be time consuming when implemented on embedded hardware systems.

Most communication systems employ Viterbi decoding involving data packets of fixed sizes, with a fixed bit/byte pattern either at the beginning or/and at the end of the data packet. By using the known bit/byte pattern as reference, the start node may be set to a fixed value, thereby obtaining a perfect Maximum Likelihood Path during traceback.

Limitations

A physical implementation of a Viterbi decoder will not yield an exact maximum-likelihood stream due to quantization of the input signal, branch and path metrics, and finite traceback length. Practical implementations do approach within 1 dB of the ideal.

The output of a Viterbi decoder, when decoding a message damaged by an additive Gaussian channel, has errors grouped in error bursts. Single-error-correcting codes alone can't correct such bursts, so either the convolutional code and the Viterbi decoder must be designed powerful enough to drive down errors to an acceptable rate, or burst error-correcting codes must be used.

Punctured codes

A hardware viterbi decoder of punctured codes is commonly implemented in such a way:

  • A depuncturer, which transforms the input stream into the stream which looks like an original (non punctured) stream with ERASE marks at the places where bits were erased.
  • A basic Viterbi decoder understanding these ERASE marks (that is, not using them for branch metric calculation).

Software implementation

Main article: Viterbi algorithm

One of the most time-consuming operations is an ACS butterfly, which is usually implemented using assembly language and an appropriate instruction set extensions (such as SSE2) to speed up the decoding time.

Applications

The Viterbi decoding algorithm is widely used in the following areas:

References

  1. B. Moision, "A truncation depth rule of thumb for convolutional codes," 2008 Information Theory and Applications Workshop, San Diego, CA, 2008, pp. 555-557, doi:10.1109/ITA.2008.4601052.
  2. Stefan Host, Rolf Johannesson, Dmitrij K. Zigangirod, Kamil Sh. Zigangirod, and Viktor V. Zyablod. "On the Distribution of the Output Error Burst Lengths for Viterbi Decoding of Convolutional Codes".
  3. Curry, S. J.; Harmon, W. D. "A bound on Viterbi decoder error burst length".

External links

Categories: