Misplaced Pages

In physical oceanography and fluid dynamics, the wind stress is the shear stress exerted by the wind on the surface of large bodies of water – such as oceans, seas, estuaries and lakes. When wind is blowing over a water surface, the wind applies a wind force on the water surface. The wind stress is the component of this wind force that is parallel to the surface per unit area. Also, the wind stress can be described as the flux of horizontal momentum applied by the wind on the water surface. The wind stress causes a deformation of the water body whereby wind waves are generated. Also, the wind stress drives ocean currents and is therefore an important driver of the large-scale ocean circulation. The wind stress is affected by the wind speed, the shape of the wind waves and the atmospheric stratification. It is one of the components of the air–sea interaction, with others being the atmospheric pressure on the water surface, as well as the exchange of energy and mass between the water and the atmosphere.

Background

Stress is the quantity that describes the magnitude of a force that is causing a deformation of an object. Therefore, stress is defined as the force per unit area and its SI unit is the Pascal. When the deforming force acts parallel to the object's surface, this force is called a shear force and the stress it causes is called a shear stress.

Dynamics

Wind blowing over an ocean at rest first generates small-scale wind waves which extract energy and momentum from the wave field. As a result, the momentum flux (the rate of momentum transfer per unit area per unit time) generates a current. These surface currents are able to transport energy (e.g. heat) and mass (e.g. water or nutrients) around the globe. The different processes described here are depicted in the sketches shown in figures 1.1 till 1.4. Interactions between wind, wind waves and currents are an essential part of the world ocean dynamics. Eventually, the wind waves also influence the wind field leading to a complex interaction between wind and water whereof the research for a correct theoretical description is ongoing. The Beaufort scale quantifies the correspondence between wind speed and different sea states. Only the top layer of the ocean (mixed layer) is stirred by the wind stress. This upper layer of the ocean has a depth on the order of 10m.

The wind blowing parallel to a water surface deforms that surface as a result of shear action caused by the fast wind blowing over the stagnant water. The wind blowing over the surface applies a shear force on the surface. The wind stress is the component of this force that acts parallel to the surface per unit area. This wind force exerted on the water surface due to shear stress is given by:

${\displaystyle {\begin{aligned}F_{x}&={\frac {1}{\rho }}{\frac {\partial \tau _{x}}{\partial z}},\\F_{y}&={\frac {1}{\rho }}{\frac {\partial \tau _{y}}{\partial z}}.\end{aligned}}}$

Here, F represents the shear force per unit mass (default), ${\displaystyle \rho }$ represents the air density and ${\displaystyle \tau }$ represents the wind shear stress. Furthermore, z is the lifting direction as x corresponds to the zonal direction, y corresponds to the meridional direction. The vertical derivatives of the wind stress components are also called the vertical eddy viscosity. The equation describes how the force exerted on the water surface decreases for a denser atmosphere or, to be more precise, a denser atmospheric boundary layer (this is the layer of a fluid where the influence of friction is felt). On the other hand, the exerted force on the water surface increases when the vertical eddy viscosity increases. The wind stress can also be described as a downward transfer of momentum and energy from the air to the water.

The magnitude of the wind stress (${\displaystyle \tau }$) is often parametrized as a function of wind speed ${\displaystyle U_{h}}$ at a certain height ${\displaystyle h}$ above the surface in the form

${\displaystyle \tau _{\text{wind}}=\rho _{\text{air}}C_{D}U_{h}^{2}.}$

Here, ${\displaystyle \rho _{\text{air}}}$ is the density of the surface air and C_D is a dimensionless wind drag coefficient which is a repository function for all remaining dependencies. An often used value for the drag coefficient is ${\displaystyle C_{D}=0.0015}$. Since the exchange of energy, momentum and moisture is often parametrized using bulk atmospheric formulae, the equation above is the semi-empirical bulk formula for the surface wind stress. The height at which the wind speed is referred to in wind drag formulas is usually 10 meters above the water surface. The formula for the wind stress explains how the stress increases for a denser atmosphere and higher wind speeds.

When shear force caused by stress is in balance with the Coriolis force, this can be written as:

${\displaystyle {\begin{aligned}\Sigma F_{x}={\frac {1}{\rho }}{\frac {\partial \tau _{x}}{\partial z}}+fv=0,\\-fv&={\frac {1}{\rho }}{\frac {\partial \tau _{x}}{\partial z}};\\\Sigma F_{y}={\frac {1}{\rho }}{\frac {\partial \tau _{y}}{\partial z}}-fu=0,\\fu&={\frac {1}{\rho }}{\frac {\partial \tau _{y}}{\partial z}}.\end{aligned}}}$

where f is the Coriolis parameter, u and v are respectively the zonal and meridional currents and ${\displaystyle +fv}$ and ${\displaystyle -fu}$ are respectively the zonal Coriolis forces and meridional Coriolis forces.

This balance of forces is known as the Ekman balance. Some important assumptions that underlie the Ekman balance are that there are no boundaries, an infinitely deep water layer, constant vertical eddy viscosity, barotropic conditions with no geostrophic flow and a constant Coriolis parameter. The oceanic currents that are generated by this balance are referred to as Ekman currents. In the Northern Hemisphere, Ekman currents at the surface are directed with an angle of 45° to the right of the wind stress direction and in the Southern Hemisphere they are directed with the same angle to the left of the wind stress direction. Flow directions of deeper positioned currents are deflected even more to the right in the Northern Hemisphere and to the left in the Southern Hemisphere. This phenomenon is called the Ekman spiral.

The Ekman transport can be obtained from vertically integrating the Ekman balance, giving:

${\displaystyle {\begin{aligned}U_{E}&={\frac {\tau _{y}}{f\rho D}},\\V_{E}&=-{\frac {\tau _{x}}{f\rho D}},\end{aligned}}}$

where D is the depth of the Ekman layer. Depth-averaged Ekman transport is directed perpendicular to the wind stress and, again, directed to the right of the wind stress direction in the Northern Hemisphere and to the left of the wind stress direction in the Southern Hemisphere. Alongshore winds therefore generate transport towards or away from the coast. For small values of D, water can return from or to deeper water layers, resulting in Ekman up- or downwelling. Upwelling due to Ekman transport can also happen at the equator due to the change of sign of the Coriolis parameter in the Northern and Southern Hemisphere and the stable easterly winds that are blowing to the North and South of the equator.

Due to the strong temporal variability of the wind, the wind forcing on the ocean surface is also highly variable. This is one of the causes of the internal variability of ocean flows as these changes in the wind forcing cause changes in the wave field and the thereby generated currents. Variability of ocean flows also occurs because the changes of the wind forcing are disturbances of the mean ocean flow, which leads to instabilities. A well known phenomenon that is caused by changes in surface wind stress over the tropical Pacific is the El Niño-Southern Oscillation (ENSO).

Global wind stress patterns

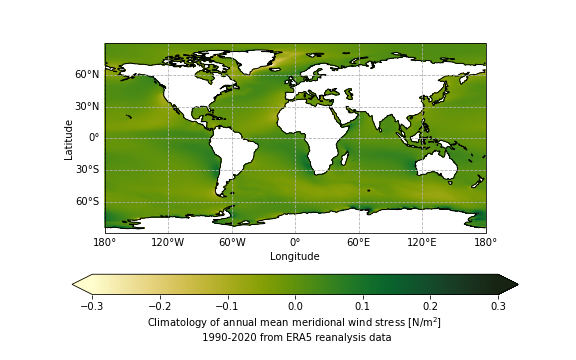
The global annual mean wind stress forces the global ocean circulation. Typical values for the wind stress are about 0.1Pa and, in general, the zonal wind stress is stronger than the meridional wind stress as can be seen in figures 2.1 and 2.2. It can also be seen that the largest values of the wind stress occur in the Southern Ocean for the zonal direction with values of about 0.3Pa. Figures 2.3 and 2.4 show that monthly variations in the wind stress patterns are only minor and the general patterns stay the same during the whole year. It can be seen that there are strong easterly winds (i.e. blowing toward the West), called easterlies or trade winds near the equator, very strong westerly winds at midlatitudes (between ±30° and ±60°), called westerlies, and weaker easterly winds at polar latitudes. Also, on a large annual scale, the wind-stress field is fairly zonally homogeneous. Important meridional wind stress patterns are northward (southward) currents on the eastern (western) coasts of continents in the Northern Hemisphere and on the western (eastern) coast in the Southern Hemisphere since these generate coastal upwelling which causes biological activity. Examples of such patterns can be observed in figure 2.2 on the East coast of North America and on the West coast of South America.

Large-scale ocean circulation

Wind stress in one of the drivers of the large-scale ocean circulation with other drivers being the gravitational pull exerted by the Moon and Sun, differences in atmospheric pressure at sea level and convection resulting from atmospheric cooling and evaporation. However, the contribution of the wind stress to the forcing of the oceanic general circulation is largest. Ocean waters respond to the wind stress because of their low resistance to shear and the relative consistence with which winds blow over the ocean. The combination of easterly winds near the equator and westerly winds at midlatitudes drives significant circulations in the North and South Atlantic Oceans, the North and South Pacific Oceans and the Indian Ocean with westward currents near the equator and eastward currents at midlatitudes. This results in characteristic gyre flows in the Atlantic and Pacific consisting of a subpolar and subtropical gyre. The strong westerlies in the Southern ocean drive the Antarctic Circumpolar Current which is the dominant current in the Southern Hemisphere whereof no comparable current exists in the Northern Hemisphere.

The equations to describe large-scale ocean dynamics were formulated by Harald Sverdrup and came to be known as Sverdrup dynamics. Important is the Sverdrup balance which describes the relation between the wind stress and the vertically integrated meridional transport of water. Other significant contributions to the description of large-scale ocean circulation were made by Henry Stommel who formulated the first correct theory for the Gulf Stream and theories of the abyssal circulation. Long before these theories were formulated, mariners have been aware of the major surface ocean currents. As an example, Benjamin Franklin already published a map of the Gulf Stream in 1770 and in European discovery of the gulf stream dates back to the 1512 expedition of Juan Ponce de León. Apart from such hydrographic measurement there are two methods to measure the ocean currents directly. Firstly, the Eulerian velocity can be measured using a current meter along a rope in the water column. And secondly, a drifter can be used which is an object that moves with the currents whereof the velocity can be measured.

Wind-driven upwelling

Wind-driven upwelling brings nutrients from deep waters to the surface which leads to biological productivity. Therefore, wind stress impacts biological activity around the globe. Two important forms of wind-driven upwelling are coastal upwelling and equatorial upwelling.

Coastal upwelling occurs when the wind stress is directed with the coast on its left (right) in the Northern (Southern) Hemisphere. If so, Ekman transport is directed away from the coast forcing waters from below to move upward. Well known coastal upwelling areas are the Canary Current, the Benguela Current, the California Current, the Humboldt Current, and the Somali Current. All of these currents support major fisheries due to the increased biological activities.

Equatorial upwelling occurs due to the trade winds blowing towards the west in both the Northern Hemisphere and the Southern Hemisphere. However, the Ekman transport that is associated with these trade winds is directed 90° to the right of the winds in the Northern Hemisphere and 90° to the left of the winds in the Southern Hemisphere. As a result, to the North of the equator water is transported away from the equator and to the South of the equator water is transported away from the equator. This horizontal divergence of mass has to be compensated and hence upwelling occurs.

Wind waves

Wind waves are waves at the water surface that are generated due to the shear action of wind stress on the water surface and the aim of gravity, that acts as a restoring force, to return the water surface to its equilibrium position. Wind waves in the ocean are also known as ocean surface waves. The wind waves interact with both the air and water flows above and below the waves. Therefore, the characteristics of wind waves are determined by the coupling processes between the boundary layers of both the atmosphere and ocean. Wind waves also play an important role themselves in the interaction processes between the ocean and the atmosphere. Wind waves in the ocean can travel thousands of kilometers. A proper description of the physical mechanisms that cause the growth of wind waves and is in accordance with observations has yet to be completed. A necessary condition for wind waves to grow is a minimum wind speed of 0.05 m/s.

Expressions for the drag coefficient

The drag coefficient is a dimensionless quantity which quantifies the resistance of the water surface. Due to the fact that the drag coefficient depends on the past of the wind, the drag coefficient is expressed differently for different time and spatial scales. A general expression for the drag coefficient does not yet exist and the value is unknown for unsteady and non-ideal conditions. In general, the drag coefficient increases with increasing wind speed and is greater for shallower waters. The geostrophic drag coefficient is expressed as:

${\displaystyle C_{g}={\frac {\tau }{U_{g}^{2}}},}$

where ${\displaystyle U_{g}}$ is the geostrophic wind which is given by:

${\displaystyle U_{g}={\frac {1}{\rho f}}{\frac {\partial p}{\partial y}}.}$

In global climate models, often a drag coefficient appropriate for a spatial scale of 1° by 1° and a monthly time scale is used. In such a timescale, the wind can strongly fluctuate. The monthly mean shear stress can be expressed as:

${\displaystyle \langle \tau \rangle =\rho \langle C_{D}\rangle \langle U\rangle ^{2}\left(1+{\frac {\langle U'^{2}\rangle }{\langle U\rangle ^{2}}}\right),}$

where ${\displaystyle \rho }$ is the density, ${\displaystyle C_{D}}$ is the drag coefficient, ${\displaystyle \langle U\rangle }$ is the monthly mean wind and U' is the fluctuation from the monthly mean.

${\displaystyle C_{D}=1.3\times 10^{-3}\left(1+{\frac {\langle U'^{2}\rangle }{\langle U\rangle ^{2}}}\right).}$

Measurements

It is not possible to directly measure the wind stress on the ocean surface. To obtain measurements of the wind stress, another easily measurable quantity like wind speed is measured and then via a parametrization the wind stress observations are obtained. Still, measurements of the wind stress are important as the value of the drag coefficient is not known for unsteady and non-ideal conditions. Measurements of the wind stress for such conditions can resolve the issue of the unknown drag coefficient. Four methods of measuring the drag coefficient are known as the Reynolds stress method, the dissipation method, the profile method and a method of using radar remote sensing.

Wind stress on land surface

The wind can also exert a stress force on land surface which can lead to erosion of the ground.

References

1. ^ Dijkstra, Henk A (2008). Dynamical oceanography. Springer Science and Business Media.
2. ^ Jones, Ian SF; Yoshiaki (2001). Wind stress over the ocean. Cambridge University Press.
3. Young, Hugh D; Freedman, Roger A (1996). University physics. Vol. 15. Addison-Wesley Reading, MA.
4. ^ Cushman-Roisin, Benoit; Beckers, Jean-Marie (2011). Introduction to geophysical fluid dynamics: physical and numerical aspects. Academic press.
5. ^ Marsh, Robert; van Sebille, Erik (2021). Ocean Currents: Physical Drivers in a Changing World. Vol. 1. Elsevier.
6. Smith, Stuart D. (1988). "Coefficients for sea surface wind stress, heat flux, and wind profiles as a function of wind speed and temperature". J. Geophys. Res. 93 (C12): 15467. Bibcode:1988JGR....9315467S. doi:10.1029/JC093iC12p15467.
7. Trenberth, Kevin E; Large, William G; Olson, Jerry G (1990). "The mean annual cycle in global ocean wind stress". Journal of Physical Oceanography. 20 (11): 1742. Bibcode:1990JPO....20.1742T. doi:10.1175/1520-0485(1990)020<1742:TMACIG>2.0.CO;2.
8. Ekman, Vagn Walfrid (1905). "On the influence of the earth's rotation on ocean-currents". Almqvist \& Wiksells boktryckeri, A.-B. {{cite journal}}: Cite journal requires |journal= (help)
9. ^ Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; Schepers, D.; Simmons, A.; Soci, C.; Dee, D.; Thépaut, J-N. (2019). ERA5 monthly averaged data on single levels from 1979 to present. (Accessed on < 22-06-2021 >. Copernicus Climate Change Service (C3S) Climate Data Store (CDS).
10. Sverdrup, Harald Ulrich (1947). "Wind-driven currents in a baroclinic ocean; with application to the equatorial currents of the eastern Pacific". Proceedings of the National Academy of Sciences of the United States of America. 33 (11): 318–326. Bibcode:1947PNAS...33..318S. doi:10.1073/pnas.33.11.318. PMC 1079064. PMID 16588757.
11. Stommel, Henry (1948). "The westward intensification of wind-driven ocean currents". Eos, Transactions American Geophysical Union. 29 (2). Wiley Online Library: 202–206. Bibcode:1948TrAGU..29..202S. doi:10.1029/TR029i002p00202.
12. Stommel, Henry; Arons, Arnold B. (1959). "On the abyssal circulation of the world ocean—I. Stationary planetary flow patterns on a sphere". Deep Sea Research. 6. Elsevier: 140–154. doi:10.1016/0146-6313(59)90065-6.
13. Stommel, Henry; Arons, Arnold B. (1959). "On the abyssal circulation of the world ocean—II. An idealized model of the circulation pattern and amplitude in oceanic basins". Deep Sea Research. 6. Elsevier: 217–233. Bibcode:1959DSR.....6..217S. doi:10.1016/0146-6313(59)90075-9.
14. Richardson, Philip L (1980). "Benjamin Franklin and Timothy Folger's first printed chart of the Gulf Stream". Science. 207 (4431). American Association for the Advancement of Science: 643–645. Bibcode:1980Sci...207..643R. doi:10.1126/science.207.4431.643. PMID 17749327. S2CID 31388621.
15. Fernandez-Armesto, Felipe (2006). Pathfinders: A Global History of Exploration. W. W. Norton & Company. p. 194. ISBN 978-0-393-06259-5.
16. Young, Ian R (1999). Wind generated ocean waves. Elsevier.
17. de Swart, H.E. (2019). Ocean waves - lecture notes. Utrecht University - The Netherlands.
18. Komen, Gerbrand J.; Cavaleri, Luigi; Donelan, Mark; Hasselman, Klaus; Hasselman, S; Janssen, P. A. E. M. (1996). Dynamics and modelling of ocean waves.

• Fluid dynamics
• Physical oceanography