In mathematics, the complex Witt algebra, named after Ernst Witt, is the Lie algebra of meromorphic vector fields defined on the Riemann sphere that are holomorphic except at two fixed points. It is also the complexification of the Lie algebra of polynomial vector fields on a circle, and the Lie algebra of derivations of the ring C.
There are some related Lie algebras defined over finite fields, that are also called Witt algebras.
The complex Witt algebra was first defined by Élie Cartan (1909), and its analogues over finite fields were studied by Witt in the 1930s.
Basis
A basis for the Witt algebra is given by the vector fields , for n in .
The Lie bracket of two basis vector fields is given by
This algebra has a central extension called the Virasoro algebra that is important in two-dimensional conformal field theory and string theory.
Note that by restricting n to 1,0,-1, one gets a subalgebra. Taken over the field of complex numbers, this is just the Lie algebra of the Lorentz group . Over the reals, it is the algebra sl(2,R) = su(1,1). Conversely, su(1,1) suffices to reconstruct the original algebra in a presentation.
Over finite fields
Over a field k of characteristic p>0, the Witt algebra is defined to be the Lie algebra of derivations of the ring
- k/z
The Witt algebra is spanned by Lm for −1≤ m ≤ p−2.
Images
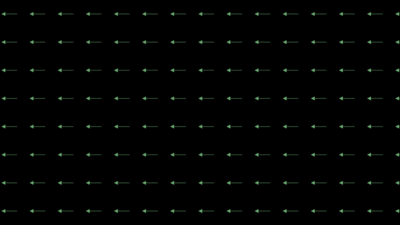 n = -1 Witt vector field
n = -1 Witt vector field n = 0 Witt vector field
n = 0 Witt vector field n = 1 Witt vector field
n = 1 Witt vector field
 n = -2 Witt vector field
n = -2 Witt vector field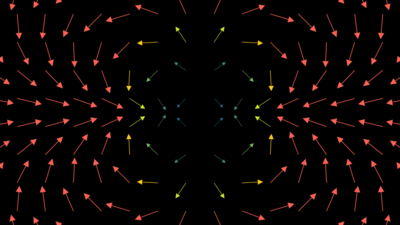 n = 2 Witt vector field
n = 2 Witt vector field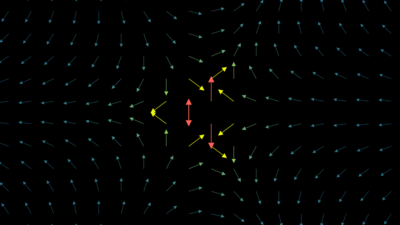 n = -3 Witt vector field
n = -3 Witt vector field
See also
References
- D Fairlie, J Nuyts, and C Zachos (1988). Phys Lett B202 320-324. doi:10.1016/0370-2693(88)90478-9
- Élie Cartan, Les groupes de transformations continus, infinis, simples. Ann. Sci. Ecole Norm. Sup. 26, 93-161 (1909).
- "Witt algebra", Encyclopedia of Mathematics, EMS Press, 2001
 , for n in
, for n in  .
.

 of the
of the  . Over the reals, it is the algebra
. Over the reals, it is the algebra