| This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources. Find sources: "Woo circles" – news · newspapers · books · scholar · JSTOR (May 2024) |
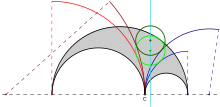
In geometry, the Woo circles, introduced by Peter Y. Woo, are a set of infinitely many Archimedean circles.
Construction
Form an arbelos with the two inner semicircles tangent at point C. Let m denote any nonnegative real number. Draw two circles, with radii m times the radii of the smaller two arbelos semicircles, centered on the arbelos ground line, also tangent to each other at point C and with radius m times the radius of the corresponding small arbelos arc. Any circle centered on the Schoch line and externally tangent to the circles is a Woo circle.
See also
References
- Thomas Schoch (2007). "Arbelos - The Woo Circles". Retrieved 2008-06-05.
This elementary geometry-related article is a stub. You can help Misplaced Pages by expanding it. |