Misplaced Pages

Zero-symmetric graph

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
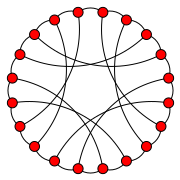
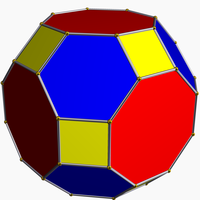18-vertex zero-symmetric graphThe smallest zero-symmetric graph, with 18 vertices and 27 edgesTruncated cuboctahedronThe truncated cuboctahedron, a zero-symmetric polyhedron
Graph families defined by their automorphisms
distance-transitive → distance-regular ← strongly regular
↓
symmetric (arc-transitive) ← t-transitive, t ≥ 2 skew-symmetric
↓
(if connected)
vertex- and edge-transitive 		→ edge-transitive and regular → edge-transitive
↓ ↓ ↓
vertex-transitive → regular → (if bipartite)
biregular
↑
Cayley graph ← zero-symmetric asymmetric

In the mathematical field of graph theory, a zero-symmetric graph is a connected graph in which each vertex has exactly three incident edges and, for each two vertices, there is a unique symmetry taking one vertex to the other. Such a graph is a vertex-transitive graph but cannot be an edge-transitive graph: the number of symmetries equals the number of vertices, too few to take every edge to every other edge.

The smallest zero-symmetric graph with two edge orbits

The name for this class of graphs was coined by R. M. Foster in a 1966 letter to H. S. M. Coxeter. In the context of group theory, zero-symmetric graphs are also called graphical regular representations of their symmetry groups.

Examples

The smallest zero-symmetric graph is a nonplanar graph with 18 vertices. Its LCF notation is .

Among planar graphs, the truncated cuboctahedral and truncated icosidodecahedral graphs are also zero-symmetric.

These examples are all bipartite graphs. However, there exist larger examples of zero-symmetric graphs that are not bipartite.

These examples also have three different symmetry classes (orbits) of edges. However, there exist zero-symmetric graphs with only two orbits of edges. The smallest such graph has 20 vertices, with LCF notation .

Properties

Every finite zero-symmetric graph is a Cayley graph, a property that does not always hold for cubic vertex-transitive graphs more generally and that helps in the solution of combinatorial enumeration tasks concerning zero-symmetric graphs. There are 97687 zero-symmetric graphs on up to 1280 vertices. These graphs form 89% of the cubic Cayley graphs and 88% of all connected vertex-transitive cubic graphs on the same number of vertices.

Unsolved problem in mathematics: Does every finite zero-symmetric graph contain a Hamiltonian cycle? (more unsolved problems in mathematics)

All known finite connected zero-symmetric graphs contain a Hamiltonian cycle, but it is unknown whether every finite connected zero-symmetric graph is necessarily Hamiltonian. This is a special case of the Lovász conjecture that (with five known exceptions, none of which is zero-symmetric) every finite connected vertex-transitive graph and every finite Cayley graph is Hamiltonian.

See also

  • Semi-symmetric graph, graphs that have symmetries between every two edges but not between every two vertices (reversing the roles of edges and vertices in the definition of zero-symmetric graphs)

References

  1. Coxeter, Harold Scott MacDonald; Frucht, Roberto; Powers, David L. (1981), Zero-symmetric graphs, Academic Press, Inc. , New York-London, ISBN 0-12-194580-4, MR 0658666
  2. Coxeter, Frucht & Powers (1981), p. ix.
  3. Lauri, Josef; Scapellato, Raffaele (2003), Topics in Graph Automorphisms and Reconstruction, London Mathematical Society Student Texts, Cambridge University Press, p. 66, ISBN 9780521529037.
  4. Coxeter, Frucht & Powers (1981), Figure 1.1, p. 5.
  5. Coxeter, Frucht & Powers (1981), pp. 75 and 80.
  6. Coxeter, Frucht & Powers (1981), p. 55.
  7. Conder, Marston D. E.; Pisanski, Tomaž; Žitnik, Arjana (2017), "Vertex-transitive graphs and their arc-types", Ars Mathematica Contemporanea, 12 (2): 383–413, arXiv:1505.02029, doi:10.26493/1855-3974.1146.f96, MR 3646702
  8. Potočnik, Primož; Spiga, Pablo; Verret, Gabriel (2013), "Cubic vertex-transitive graphs on up to 1280 vertices", Journal of Symbolic Computation, 50: 465–477, arXiv:1201.5317, doi:10.1016/j.jsc.2012.09.002, MR 2996891.
  9. Coxeter, Frucht & Powers (1981), p. 10.
Categories: